We have already considered with disfavour the possibility of the universe having been planned by a biologist or an engineer; from the intrinsic evidence of his creation, the Great Architect of the Universe now begins to appear as a pure mathematician.
~Sir James Jeans
The 254th day of the year; 254 is the maximum number of pieces a flat pizza could be cut into with n straight lines.... find n. (for help, see bottom of this post, a good quadratic problem)
254 is the average of consecutive primes,
and 254 = 28 - 21
Probability Fact @ProbFact points out that: Odds of drawing a straight in a 5-card hand: 254 to 1.
1632 Torricelli's first letter to Galileo. "We have direct evidence on the scope and trend of Torricelli’s scientific studies during his stay at Rome in the first letter (11 September 1632) of his surviving correspondence, addressed to Galileo on behalf of Castelli, who was away from Rome. In acknowledging receipt of a letter from Galileo to Castelli, Torricelli seized the opportunity to introduce himself as a mathematician by profession, well versed in the geometry of Apollonius, Archimedes, and Theodosius; he added that he had studied Ptolemy and had seen “nearly everything” by Brahe, Kepler, and Longomontanus. These studies had compelled him to accept the Copernican doctrine and to become “a Galileist by profession and sect”; he had been the first in Rome to make a careful study of Galileo’s Dialogo sopra i due massimi sistemi, published in February of that year (1632).*encyclopedia.com
After Torricelli's father died, between 1626 and 1627 he traveled to Rome with his whole family (his mother and two brothers) to study with the Benedictine friar, Benedetto Castelli.
Torricelli would be assigned the position of private secretary of Castelli. He used the money obtained with work to pay for his studies so he could stay in the position and studying at the University College of Sapienza until 1632. Later, Castelli appointed Torricelli to replace him as the teacher in mathematics, mechanics, hydraulics, and astronomy in the University College of Sapienza.
 |
| *Torricelli w/ barometer *Chemistry World |
1789 Alexander Hamilton appointed the first secretary of the U.S. Treasury. It is because of him that we did not adopt the English system of counting money, but a decimal system instead. *VFR Certainly it is hazardous to give one person credit for any decision in a democracy. For example, in 1784 Thomas Jefferson had proposed a decimal currency system based on the Spanish dollar, with coins for 10 dollars, 1 dollar, 1/10 dollar, and 1/100 dollar; possibly supplemented by a half-dollar, "double tenth", and "five copper piece". One argument he advanced in favor of this system was that the 1/100-dollar coin would be similar in value to existing copper coins. The Spanish Dollar was already in fairly common use in the US. *Wik
The name "dollar" originates from Bohemia and a 29 g silver-coin called the Joachimsthaler. North American colonist commonly used the Spanish peso or "piece of eight" (its value was 8 reales) has always held first place, and this coin was also called the "dollar" as early as 1581. Spanish dollars or "pieces of eight" were distributed widely in the Spanish colonies in the New World. The dollar was derived from shortening the name of the city in the valley where the silver was mined named after Saint Joachim. The coins were called Joachimsthaler (From the valley of Saint Joachim). This mouthful became shortened in common usage to thaler or taler, and then eventually to dollar.
The origin of the dollar symbol, $, was adopted from the Spanish abbreviation for pesos, "ps". There seem to have been much flexibility in how it was written as the 1776 diary of Ezra l'Hommedieu, a member of the New York Provencial Assembly had over a dozen different symbols in his diary beginning with a single vertical bar and proceeding to two vertical bars. *F Carjori
The image of l'Hommedieu's diary from Cajori's History of Mathematical Notations
The earliest U.S. dollar coins did not have any dollar symbol. The first occurrence in print is claimed to be from 1790s, by a Philadelphia printer Archibald Binny. The $1 United States Note issued by the United States in 1869 included a large symbol consisting of a "U" with the right bar overlapping an "S" like a single-bar dollar sign, as well as a very small double-stroke dollar sign in the legal warning against forgery.
(If any one has an image of this coin I would love a copy. Many early U S Dollar coins had no denomination on them at all, and no sign of the dollar symbol on any I have seen.
1820 André Marie Ampere (1775-1836) was professor of mathematics at the École Polytechnique from 1809. On 11 September 1820 he heard of H. C. Ørsted's discovery that a magnetic needle is acted on by a voltaic current. Only a week later, on 18 September, Ampère presented a paper to the Academy containing a much more complete exposition of that and kindred phenomena. On the same day, Ampère also demonstrated before the Academy that parallel wires carrying currents attract or repel each other, depending on whether currents are in the same (attraction) or in opposite directions (repulsion). This laid the foundation of electrodynamics.*Wik
In 1822, it was announced by the College of Cardinals that henceforth "the printing and publication of works treating of the motion of the earth and the stability of the sun, in accordance with the opinion of modern astronomers, is permitted." When in two weeks pope Pius VII ratified the Cardinals' decree, the Catholic Church finally officially accepted the Copernican principle that on 22 Jun 1633 Italian scientist Galileo had been imprisoned for championing.(This is an over-generalization of the charges against Galileo.) It was not until 1835 that the Vatican removed Galileo's Dialogue Concerning the Two Chief World Systems from its list of banned books. Finally 31 Oct 1992, the Catholic Church admitted that Galileo had been correct. *TIS
In 1831, Charles Darwin and Captain Robert Fitzroy traveled from London to Plymouth to inspect the Beagle. This was Darwin's first sight of the ship on which he would sail on a voyage of discovery leading to his famous theory of evolution. *TIS
1831 After a four hour disputation in Latin, Jacobi was appointed professor at the University of K¨onigsburg. While there he inaugurated what was then a complete novelty in mathematics— research seminars—assembling the more advanced students and interested colleagues. [DSB 7, 50] *VFR
1893 Edgeworth sends greetings to Karl Pearson, "I hope that you flourish in Probabilities." *The History of Statistics: The Measurement of Uncertainty Before 1900
By Stephen M. Stigle
1923 Sixteen year old Donald Coxeter writes to Eric H. Neville (who had worked with Ramanujan) at the request of Literary scholar and suffragette, Edith Morley. "I am going to buy your book on the Fourth Dimension as I am awfully keen on that sort of thing. I am writing a book on 'Dimensional Analogy' of which I enclose an outline." Neville met with Coxeter and after a brief interview advised that, "You must leave school at once! They're not teaching you right!" He had him tutored by Alan Robson, Master at Marlborough College near Stonehenge. *Siobhan Roberts, King of Infinite Space
1933 In a speech at British Association meeting, Ernest Rutherford confidently dismissed the possibility of atomic energy. In a 2011 paper , John G Jenkins wrote "In the 1930s Ernest Rutherford (1871–1937) repeatedly suggested, sometimes angrily, that the possibility of harnessing atomic energy was “moonshine.” Yet, as war approached he secretly advised the British government to “keep an eye on the matter.” I suggest that Rutherford did not really believe his “moonshine” claim but did have profound reasons for making it. If I am correct, then this casts additional light on his personality, stature, and career." *Physics in Perspective
1940 The first remote computation -- from Dartmouth College to AT&T Bell Laboratories -- is demonstrated during a meeting of the American Mathematical Association. At Dartmouth, George Stibitz set up a terminal that allowed attendees to perform remote calculation by telegraph wire with the Complex Calculator in New York City. Stibitz had first tested the connection on September 9, an event memorialized by a plaque in front of McNutt Hall at Dartmouth College.*CHM
1958 Jack Kilby successfully tests the first integrated circuit at Texas Instruments to prove that resistors and capacitors could exist on the same piece of semiconductor material. His circuit consisted of a sliver of germanium with five components linked by wires. Along with Bob Noyce, he is considered the inventor of the integrated circuit (IC). *CHM
1981 NBC Magazine broadcasts a story about Rubik's cube on TV. The cube had begun production in 1977 in Hungary and after a couple of years began to sweep across Europe. In 1981, the rage hit the US. In November of 1981, the US would hold 1st American Rubik's Cube Championships. *Mark Longridge, A Rubik's Cube Chronology
In 1997, the Mars Global Surveyor, launched in Nov 1996, went into an elliptical orbit around Mars. To drop into a lower orbit the original mission plan was to use a braking effect by dipping into the upper Martian atmosphere. The lower orbit was a better position for mapping purposes. However, the aerobraking method originally planned was suspended for several weeks to give engineers time to develop more gentle manoeuvers to protect the craft when a solar array failed to deploy correctly, and was flexing excessively. It was to spend two years mapping the surface of Mars. *TIS
 |
| *Gunter's Space Page |
1623 Stephano Angeli (21 Sept 1623 in Venice - 11 Oct 1697 )was an Italian mathematician who worked on infinitesimals and used them to study spirals, parabolas and hyperbolas.(James)Gregory studied with Angeli in Padua from 1664 to 1668 and learnt from him about series expansions of functions. *SAU The word abscissa is first recorded in 1659 Angeli, according to Moritz Cantor.
1798 Franz Ernst Neumann (September 11, 1798 – May 23, 1895) was a German mineralogist, physicist and mathematician.
Neumann was born in Joachimsthal, Margraviate of Brandenburg, located not far from Berlin. In 1815 he interrupted his studies at Berlin to serve as a volunteer in the Hundred Days against Napoleon, and was wounded in the Battle of Ligny. Subsequently he entered Berlin University as a student of theology, but soon turned to scientific subjects. His earlier papers were mostly concerned with crystallography, and the reputation they gained him led to his appointment as Privatdozent at the University of Königsberg, where in 1828 he became extraordinary, and in 1829 ordinary, professor of mineralogy and physics. His 1831 study on the specific heats of compounds included what is now known as Neumann's Law: the molecular heat of a compound is equal to the sum of the atomic heats of its constituents.
Devoting himself next to optics, he produced memoirs which entitle him to a high place among the early searchers after a true dynamical theory of light. In 1832, by the aid of a particular hypothesis as to the constitution of the ether, he reached by a rigorous dynamical calculation results agreeing with those obtained by Augustin Louis Cauchy, and succeeded in deducing laws of double refraction closely resembling those of Augustin-Jean Fresnel. In studying double refraction, with his deduction of the elastic constants (on which the optical properties depend) Neumann employed the assumption that the symmetry of the elastic behavior of a crystal was equal to that of its form. In other words, he assumed that the magnitudes of the components of a physical property in symmetric positions are equivalent. This assumption substantially reduced the number of independent constants and greatly simplified the elastic equations. However, four decades passed before Neumann elaborated his application of symmetry in a course on elasticity in 1873. This principle was later formalized by his student Woldemar Voigt (1850–1918) in 1885: ‘‘the symmetry of the physical phenomenon is at least as high as the crystallographic symmetry,’’ which became a fundamental postulate of crystal physics known as ‘‘Neumann’s principle’’. In 1900, Voigt attributed this principle to Neumann’s 1832 paper even though, at most, all that was present in that work was an implicit assumption that the symmetry of the phenomenon was equal to that of the crystal. Bernhard Minnigerode (1837–1896), another student of Neumann, first expressed this relation in written form in 1887 in the journal Neues Jahrb. Mineral Geol. Paleontol. (Vol. 5, p. 145).
Later, Neumann attacked the problem of giving mathematical expression to the conditions holding for a surface separating two crystalline media, and worked out from theory the laws of double refraction in strained crystalline bodies. He also made important contributions to the mathematical theory of electrodynamics, and in papers published in 1845 and 1847 established mathematically the laws of the induction of electric currents. His last publication, which appeared in 1878, was on spherical harmonics (Beiträge zur Theorie der Kugelfunctionen). *Wik
1816 Carl Zeiss ( 11 September 1816 – 3 December 1888) was a German scientific instrument maker, optician and businessman. In 1846 he founded his workshop, which is still in business as Carl Zeiss AG. Zeiss gathered a group of gifted practical and theoretical opticians and glass makers to reshape most aspects of optical instrument production. His collaboration with Ernst Abbe revolutionized optical theory and practical design of microscopes. Their quest to extend these advances brought Otto Schott into the enterprises to revolutionize optical glass manufacture. The firm of Carl Zeiss grew to one of the largest and most respected optical firms in the world.*Wik
1847 Mary Watson Whitney (11 Sep 1847; 20 Jan 1921) American astronomer who trained with Maria Mitchell and succeeded her as professor and director of the Vassar College Observatory. As Mitchell had before her, Whitney championed science education the advancement of professional opportunities for women. She developed the astronomy department. Four years before her 1910 retirement, there were 160 students and eight different astronomy courses, including some of the first courses anywhere on astrophysics and on variable stars. During her tenure as director, the Observatory staff published 102 papers in major astronomical journals reporting their work on comets, asteroids, and variable stars. From 1896, photographic plates were used to study and measure star clusters.*TIS
photograph, probably from the 1880s, shows Maria (left) and Mary (right) in front of Vassar’s Almost Great Refractor. *Linda Hall org
1877 Sir James Hopwood Jeans (11 Sep 1877; 16 Sep 1946) was an English physicist, astronomer, and mathematician who was the first to propose that matter is continuously created throughout the universe. He made other innovations in astronomical theory but is perhaps best known as a writer of popular books about astronomy. Died in Dorking, Surrey.*TIS Famous quote, "We have already considered with disfavour the possibility of the universe having been planned by a biologist or an engineer; from the intrinsic evidence of his creation, the Great Architect of the Universe now begins to appear as a pure mathematician."
1884 Harvey Fletcher (11 Sep 1884; 23 Jul 1981) American acoustical engineer who was the first to demonstrate stereophonic sound (1934). He was a trail blazing investigator of the nature of speech and hearing, noted for his contributions in acoustics, electrical engineering, speech, medicine, music, atomic physics, sound pictures, and education. He guided the development of the Western Electric Hearing Aid, the first such device to use vacuum tubes. He developed a group survey method using recorded sound of decreasing volume which has wide acceptance in schools throughout the nation.*TIS
1890 Euphemia Lofton Haynes (September 11, 1890 - July 25, 1980) After graduating from Washington D.C. Miner Normal School with distinction, she went on to earn an undergraduate mathematics major (and psychology minor) from Smith College in 1914. In 1917 she married Harold Appo Haynes.
Haynes pursued graduate studies in mathematics and education at the University of Chicago, earning a masters degree in education in 1930. She continued her graduate work in mathematics at the Catholic University of America where in 1943 she became the first African-American woman to earn a Ph.D. in mathematics. Her dissertation on "The Determination of Sets of Independent Conditions Characterizing Certain Special Cases of Symmetric Correspondences" was written under the supervision of Professor Aubrey Landrey.
Euphemia Haynes devoted her life to education in the Washington, D.C. area for forty-seven years, including teaching mathematics at Armstrong High School and Dunbar High School. She became a professor of mathematics at Miner Teachers College in 1930 where she established the mathematics department and served as chair of the Division of Mathematics and Business Education (in 1955 Minor Teachers College and Wilson Teachers College united to form the District of Columbia Teachers College.) From July 1966 to July 1967, Haynes served as the first woman to chair the District of Columbia School Board. She played a central role in the integration of the DC public schools. Upon her death, she left $700,000 to the Catholic University of America which was used to establish the Euphemia Lofton Haynes Chair in the Department of Education and to support a student loan fund in the School of Education. *ASC
1930 Vera Turán Sós (11 September 1930 – 22 March 2023) was a Hungarian mathematician who specialized in number theory and combinatorics. She was a student and close collaborator of both Paul Erdős and Alfréd Rényi. She also collaborated frequently with her husband Pál Turán, an analyst, number theorist, and combinatorist. Until 1987, she worked at the Department of Analysis at the Eötvös Loránd University, Budapest. Afterwards, she was employed by the Alfréd Rényi Institute of Mathematics. She was elected a corresponding member (1985) and member (1990) of the Hungarian Academy of Sciences. In 1997, Sós was awarded the Széchenyi Prize.
One of her contributions is the Kővári–Sós–Turán theorem concerning the maximum possible number of edges in a bipartite graph that does not contain certain complete subgraphs. Another is the following so-called friendship theorem proved with Paul Erdős and Alfréd Rényi: if, in a finite graph, any two vertices have exactly one common neighbor, then some vertex is joined to all others. In number theory, Sós proved the three-gap theorem, conjectured by Hugo Steinhaus and proved independently by Stanisław Świerczkowski.
1998 Kenkichi Iwasawa (11 Sept 1917 in Shinshuku-mura (near Kiryu), Gumma Prefecture, Japan - 26 Oct 1998 in Tokyo, Japan ) In the late 1960s Iwasawa made a conjecture for algebraic number fields which, in some sense, was the analogue of the relationship which Weil had found between the zeta function and the divisor class group of an algebraic function field. This conjecture became known as "the main conjecture on cyclotomic fields" and it remained one of the most outstanding conjectures in algebraic number theory until it was solved by Mazur and Wiles in 1984 using modular curves. "it is no exaggeration to say that Iwasawa's ideas have played a pivotal role in many of the finest achievements of modern arithmetical algebraic geometry on such questions as the conjecture of B Birch and H Swinnerton-Dyer on elliptic curve; the conjecture of B Birch, J Tate, and S Lichtenbaum on the orders of the K-groups of the rings of integers of number fields; and the work of A Wiles on the modularity of elliptic curves and Fermat's Last Theorem." *SAU
1760 Louis Godin (28 February 1704 Paris – 11 September 1760 Cadiz) was a French astronomer and member of the French Academy of Sciences. He worked in Peru, Spain, Portugal and France.
He was graduated at the College of Louis le Grand, and studied astronomy under Joseph-Nicolas Delisle. His astronomical tables (1724) gave him reputation, and the French Academy of Sciences elected him a pensionary member. He was commissioned to write a continuation of the history of the academy, left uncompleted by Bernard le Bovier de Fontenelle, and was also authorized to submit to the minister, Cardinal André-Hercule de Fleury, the best means of discovering the truth in regard to the figure of the earth, and proposed sending expeditions to the equator and the polar sea. The minister approved the plan and appropriated the necessary means, the academy designating Charles Marie de La Condamine, Pierre Bouguer, and Godin to go to Peru in 1734.
When they had finished their task in 1738, at the invitation of the Viceroy of Peru, Godin accepted the professorship in mathematics in Lima, where he also established a course of astronomical lectures. When in 1746 an earthquake destroyed the greater part of Lima, he took valuable seismological observations, assisted the sufferers, and made plans by the use of which the new buildings would be less exposed to danger from renewed shocks.
In 1751 he returned to Europe, but found that he had been nearly forgotten, and superseded as pensioner of the academy; and, as his fortune had been lost in unfortunate speculations, he accepted the presidency of the college for midshipmen in Cadiz in 1752. During the earthquake of Lisbon, 1755, which was distinctly felt at Cadiz, he took observations and did much to allay the apprehensions of the public, for which he was ennobled by the king of Spain. In 1759 he was called to Paris and reinstated as pensionary member of the academy, but he died on his return to Cadiz. *Wik
1768 Joseph-Nicolas Delisle (4 Apr 1688, 11 Sep 1768) French astronomer who proposed that the series of coloured rings sometimes observed around the Sun is caused by diffraction of sunlight through water droplets in a cloud. He also worked to find the distance of the Sun from the Earth by observing transits of Venus and Mercury across the face of the Sun.*TIS
1843 Joseph Nicolas Nicollet (24 Jul 1786, 11 Sep 1843) Joseph Nicolas Nicollet was a French mathematician, explorer, and cartographer with an interest in astronomy. He was born in France, but financially ruined by the 1830 Revolution, he left for the U.S. in 1831. He made a private survey of the Mississippi region (1836-7), the results of which he presented in Washington. In 1838, he led a surveying expedition for the U.S. government party mapping out the lakes and waterways of northcentral Minnesota. He stressed to map publishers the importance of elevation marks on published maps. His maps were considered among the most accurate and useful until the surveyors for the great logging companies arrived in Minnesota's vast pine forests.*TIS
1861 Johann Martin Zacharias Dase (June 23, 1824, Hamburg – September 11, 1861, Hamburg) was a German mental calculator.
He used to spend a lot of time playing dominoes, and suggested that this played a significant role in developing his calculating skills. Dase suffered from epilepsy from early childhood throughout his life.
At age 15 he began to travel extensively, giving exhibitions in Germany, Austria and England. Among his most impressive feats, he multiplied 79532853 × 93758479 in 54 seconds. He multiplied two 20-digit numbers in 6 minutes; two 40-digit numbers in 40 minutes; and two 100-digit numbers in 8 hours 45 minutes. The famous mathematician Carl Friedrich Gauss commented that someone skilled in calculation could have done the 100-digit calculation in about half that time with pencil and paper.
These exhibitions however did not earn him enough money, so he tried to find other employments. In 1844 he obtained a position in the Railway Department of Vienna, but this didn't last long since in 1845 he was reported in Mannheim and in 1846 in Berlin.
In 1844, Dase calculated π to 200 decimal places over the course of approximately two months, a record for the time, from the Machin-like formula:
\( \frac{\pi}{4} = \arctan \frac{1}{2} + \arctan \frac{1}{5} + \arctan \frac{1}{8} \)
He also calculated a 7-digit logarithm table and extended a table of integer factorizations from 7,000,000 to 10,000,000.
Dase had very little knowledge of mathematical theory. The mathematician Julius Petersen tried to teach him some of Euclid's theorems, but gave up the task once he realized that their comprehension was beyond Dase's capabilities. Gauss however was very impressed with his calculating skill, and he recommended that the Hamburg Academy of Sciences should allow Dase to do mathematical work on a full-time basis, but Dase died shortly thereafter.
The book "Gödel, Escher, Bach" by Douglas Hofstadter mentions his calculating abilities. "... he also had an uncanny sense of quantity. That is, he could just 'tell', without counting (subitizing), how many sheep were in a field, or words in a sentence, and so forth, up to about 30." *Wik
1890 Felice Casorati (17 Dec 1835, 11 Sept 1890). He is best remembered for the Casorati-Weierstrass theorem characterizing the behavior of a function near an essential singularity.*SAU
1943 Oswald Teichmüller (18 June 1913, Nordhausen, Germany - 11 Sept 1943 on Eastern Front, WWII) His main contribution is in the area of geometric function theory.*SAU He introduced quasiconformal mappings and differential geometric methods into complex analysis.
He joined the Nazi Party in July 1931. In 1933 he organized the boycott of his Jewish professor Edmund Landau.In 1936 and 1937 he attended lectures by Nevanlinna, who sympathized with the Third Reich, where he was a guest professor and, like Brouwer, was considered by the Nazis as "politically reliable"
Much of Teichmüller's work was published in Deutsche Mathematik, a highly ideological journal founded by Ludwig Bieberbach that contained not only scholarly articles but also race propaganda. Because of the nature of the journal, his papers were hard to find in modern libraries before the publication of his collected works.
1972 Johannes de Groot (7 May 1914 , 11 Sept 1972) De Groot worked in topology and group theory. In group theory one of the topics he studied was that of groups with only trivial automorphisms. Later de Groot worked on set-theoretic topology. He introduced the concept of co-compactness and other topological concepts. *SAU
1989 W. W. Chandler (December 1, 1913, Bridport, Dorset, England; September 11, 1989) He obtained his B.Sc. from London University in 1938 by private study while working as a telephone engineer at the British Post Office Research Department. During the war he was responsible for the installation and maintenance of the Colossus at Bletchley Park. The Colossus represented the first electronic computer, however it was programmed by a mechanical switchboard. Its was used to crack the German Fish codes which guarded the highest levels of German communication. Winston Churchill characterized the Bletchley Park team as the geese who laid the golden eggs but never cackled.
After the war Chandler participated in development and installation of the MOSAIC computer and worked on optical character recognition. He died on September 11, 1989. *CHM
The Colossus team in 1981. A.W.M. Coombs, T.H. Flowers, A.C. Lynch, W.W. Chandler, N.T. Thurlow, H.W. Fensom
2012 Irving Stoy Reed (November 12, 1923 in Seattle, Washington- September 11, 2012) is a mathematician and engineer. He is best known for co-inventing a class of algebraic error-correcting and error-detecting codes known as Reed-Solomon codes in collaboration with Gustave Solomon. He also co-invented the Reed-Muller code.
Reed has made many contributions to areas of electrical engineering including radar, signal processing, and image processing. He was part of the team that built the MADDIDA, guidance system for Northrop's Snark cruise missile - one of the first digital computers. He developed and introduced the now-standard Register Transfer Language to the computer community while at M.I.T. Lincoln Laboratory. He had been a faculty member of the Electrical Engineering-Systems Department of the University of Southern California from 1962 to 1993. *Wik
**** the maximal number of pieces in which a pancake (or a circle) can be divided into by 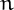 linear cuts. They are the bidimensional version of cake numbers.
linear cuts. They are the bidimensional version of cake numbers.
In general,
![\[
p_n = {n+1\choose2}+1 = {n\choose2}+ {n\choose1}+ {n\choose0}=\frac{n^2+n+2}{2}\,.
\]](https://www.numbersaplenty.com/set/pancake_number/pic.3.png)
Pancake numbers are often called lazy caterer numbers, or, more formally, central polygonal numbers.
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell





























No comments:
Post a Comment