*The image is a pumpkin carved a few Halloweens ago by Sonja L. One of my Stats/Calc students (and a really good Bassoonist, Bassooner, Bassoon-enough)~Colin Beveridge @icecolbeveridge
The 304th day of the year; 304 is the sum of six consecutive primes starting with 41, and also the sum of eight consecutive primes starting with 23. (and for those who keep up with such things, it is also the record number of wickets taken in an English cricket season by Tich Freeman in 1928.)
There are 304 semi-primes less than 2^10, but 304 is NOT one of them. *Derek Orr
304 = 77^2 - 75^2 = 23^2 - 15^2 = 40^2 - 36^2
Math Joke for Halloween: Why do mathematicians confuse Halloween and Christmas? Because Oct 31 = Dec 25 (31 in base 8 (Octal) is the same quantity as 25 in Decimal)
EVENTS
In 1815, English chemist, Sir Humphrey Davy of London (Davy was actually from Penzance) patented the miner's safety lamp. Miners at work constantly met firedamp, an explosive mix of methane gas and air, during the working of coal. This was an almost insurmountable obstacle to the working of many of the collieries until the discovery of the safety lamp. The flame of the safety lamp is surrounded by a copper or iron gauze cylinder, with openings no more than 1/24-inch. Such a fine gauze prevents flame passing through, but fails if coarser. The wire absorbs or conducts away the heat of the flame contained inside the lamp so it does not explode gas outside the lamp. If firedamp is present, a pale blue flame appears around the central flame. This warns a miner to leave the area immediately! *TIS |
| Davy Statue at Penzance |
1839 (Sometime in October) the first teacher’s institute was held at Hartford, Connecticut, 26 men teachers attended a six week course sponsored by Henry Barnard and received the “opportunity of critically reviewing the studies which they will be called upon to teach, with a full explanation of all the principles involved.” The authority who gave instruction on higher mathematics was Charles Davies. *VFR
Charles Davies (January 22, 1798 – September 17, 1876) was a professor of mathematics at the United States Military Academy, notable for writing a series of mathematical textbooks.
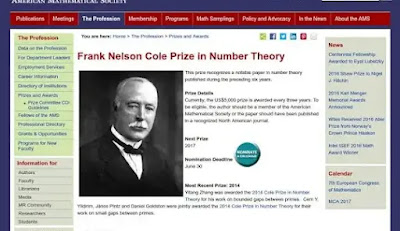
1903 At a New York meeting of the AMS F. N. Cole (1861-1927) presented a paper “On the factoring of large numbers.” He spoke not a word, but carefully raised 2 to the 67th power, then subtracted one. Moving over he computed 193,707,721 times 761,838,257,287. The calculations agreed, showing that 2^67 − 1 was not a Mersenne prime. E. T. Bell, in Mathematics—Queen and Servant of the Sciences, wrote, with his usual exaggeration, “For the first and only time on record, an audience of the American Mathematical Society vigorously applauded the author or a paper delivered before it.” Later, in 1911, Bell asked Cole how long it had taken him to find this factorization and he replied “Three years of Sundays.” It is instructive to check this arithmetic on your hand held calculator. [Eves, Adieu, 297◦; BAMS 10(1903), 134] *VFR Édouard Lucas had demonstrated in 1876 that M67 must have factors (i.e., is not prime), but he was unable to determine what those factors were,
1915 Closing date for a prize consisting of a gold medal bearing the portrait of Weierstrass and 3000 Swedish crowns for the best essay on the theory of analytic functions. King Gustav V of Sweden founded the prize to commemorate the centenary of the birth of Weierstrass. *VFR
1918 The wife of the Russian mathematician Lyapunov died of tuberculosis. On the same day, Lyapunov shot himself. He died three days later, on 3 November 1918. *VFR
1931 Herman Hupfeld wrote a well known song for the Broadway musical Everybody's Welcome which opened on October 31, 1931. In the original show, it was sung by Frances Williams. It was first recorded by Rudy Vallée on July 25, 1931 for Victor Records, then also by Jacques Renard and his Orchestra on Brunswick Records and Fred Rich. It was at first a modest hit, but was voted the second best song on the AFI's best songs of film. You know it, but if I give you the opening lyrics, you may have never heard them. But when I get to the chorus, you'll know.
This day and age we're living in
Gives cause for apprehension,
With speed and new invention
And things like fourth dimension.
Yet we get a trifle weary
With mr. einstein's theory,
So we must get down to earth at times:
Relax, relieve the tension.
And no matter what the progress
Or what may yet be proved,
The simple facts of life are such
They cannot be removed.
You must remember this,
A kiss is still a kiss,
.........As Time Goes By
 |
| Rudy Vallee |
------------------------------------------------------------------------------------------------------------
1933 Albert Einstein moved to the United States on 17 October 1933. Two weeks later, Halloween arrived. When a group of girls knocked on his door that evening and shouted 'Trick or Treat,' Einstein came to the front porch and played the violin for them: * @phalpern
In 1992, the Vatican admitted erring for over 359 years in formally condemning Galileo Galilei for entertaining scientific truths such as the Earth revolves around the sun it, which the Roman Catholic Church long denounced as anti-scriptural heresy.
After 13 years of inquiry, the Pope's commission of historic, scientific and theological scholars brought the pope a "not guilty" finding for Galileo. *TIS In 1822 the church lifted the ban on the works of Galileo and in 1979 Pope John Paul II selected a commission to investigate. On Mar 31 of 1984 the Vatican newspaper, L’Observatore Romano, stated, “The so-called heresy of Galileo does not seem to have any foundation, neither theologically nor under canon law.” It still took until Oct 31, 1992, before Pope John Paul II declared that the church
may have been mistaken in condemning Galileo. *Wik
(I can see the Papal Bull now, "Oops, Our Bad!")
BIRTHS
1711 Laura Maria Catarina Bassi (31 Oct 1711 in Bologna, Papal States, 20 Feb 1778 in Bologna, Papal States) was an Italian physicist and one of the earliest women to gain a position in an Italian university. *SAU She was the first woman in the world to earn a university chair in a scientific field of studies. She received a doctoral degree from the University of Bologna in May 1732, only the third academic qualification ever bestowed on a woman by a European university, and the first woman to earn a professorship in physics at a university in Europe. She was the first woman to be offered an official teaching position at a university in Europe.
In 1738, she married Giuseppe Veratti, a fellow academic with whom she had twelve children. After this, she was able to lecture from home on a regular basis and successfully petitioned the University for more responsibility and a higher salary to allow her to purchase her own equipment.
One of her principal patrons was Pope Benedict XIV. He supported less censorship of scholarly work, such as happened with Galileo, and he supported women figures in learning, including Agnesi.
She was mainly interested in Newtonian physics and taught courses on the subject for 28 years. She was one of the key figures in introducing Newton's ideas of physics and natural philosophy to Italy. She also carried out experiments of her own in all aspects of physics. In order to teach Newtonian physics and Franklinian electricity, topics that were not focused in the university curriculum, Bassi gave private lessons.In her lifetime, she authored 28 papers, the vast majority of these on physics and hydraulics, though she did not write any books. She published only four of her papers. Although only a limited number of her scientific works were left behind, much of her scientific impact is evident through her many correspondents including Voltaire, Francesco Algarotti, Roger Boscovich, Charles Bonnet, Jean Antoine Nollet, Giambattista Beccaria, Paolo Frisi, Alessandro Volta. Voltaire once wrote to her saying "There is no Bassi in London, and I would be much happier to be added to your Academy of Bologna than that of the English, even though it has produced a Newton". *Wik
1815 Karl (Theodor Wilhelm) Weierstrass (31 Oct 1815; 19 Feb 1897) was a German mathematician who is known as the "father of modern analysis" for his rigor in analysis led to the modern theory of functions, and considered one of the greatest mathematics teachers of all-time. He was doing mathematical research while a secondary school teacher, when in 1854, he published a paper on Abelian functions in the famous Crelle Journal. The paper so impressed the mathematical community that he shortly received an honorary doctorate and by 1856, he had a University appointment in Berlin. In 1871, he demonstrated that there exist continuous functions in an interval which have no derivatives nowhere in the interval. He also did outstanding work on complex variables. *TIS |
| *Wik |
1847 Galileo Ferraris (31 Oct 1847; 7 Feb 1897) Italian physicist who studied optics, acoustics and several fields of electrotechnics, but his most important discovery was the rotating magnetic field. He produced the field with two electromagnets in perpendicular planes, and each supplied with a current that was 90º out of phase. This could induce a current in a incorporated copper rotor, producing a motor powered by alternating current. He produced his first induction motor (with 4 poles) in May-Jun 1885. Its principles are now applied in the majority of today's a.c. motors, yet he refused to patent his invention, and preferred to place it at the service of everyone. *TIS
1890 Joseph Jean Camille Pérès (31 Oct 1890 in Clermont-Ferrand, France, 12 Feb 1962 in Paris, France) Pérès' work on analysis and mechanics was always influenced by Volterra, extending results of Volterra's on integral equations. His work in this area is now of relatively little importance since perhaps even for its day it was somewhat old fashioned.
A joint collaboration between Pérès and Volterra led to the first volume of Theorie generale des fonctionnelles published in 1936. Although the project was intended to lead to further volumes only this one was ever published. This work is discussed in where the author points out that the book belongs to an older tradition, being based on ideas introduced by Volterra himself from 1887 onwards. By the time the work was published the ideas it contained were no longer in the mainstream of development of functional analysis since topological and algebraic concepts introduced by Banach, von Neumann, Stone and others were determining the direction of the subject. However, the analysis which Pérès and Volterra studied proved important in developing ideas of mathematical physics rather than analysis and Pérès made good use of them in his applications. *SAU
1902 Abraham Wald (October 31, 1902 – December 13, 1950) was a mathematician born in Cluj, in the then Austria–Hungary (present-day Romania) who contributed to decision theory, geometry, and econometrics, and founded the field of statistical sequential analysis. He spent his researching years at Columbia University.*Wik
1919 Father Magnus J. Wenninger OSB (born Park Falls, Wisconsin, October 31, 1919) is a mathematician who works on constructing polyhedron models, and wrote the first book on their construction. *Wik
1925 John A. Pople (31 Oct 1925; 15 Mar 2004) British mathematician and chemist who, (with Walter Kohn), received the 1998 Nobel Prize in Chemistry for his work on computational methodology to study the quantum mechanics of molecules, their properties and how they act together in chemical reactions. Using Schrödinger's fundamental laws of quantum mechanics, he developed a computer program which, when provided with particulars of a molecule or a chemical reaction, outputs a description of the properties of that molecule or how a chemical reaction may take place - often used to illustrate or explain the results of different kinds of experiment. Pople provided his GAUSSIAN computer program to researchers (first published in 1970). Further developed, it is now used by thousands of chemists the world over. *TIS
1927 Narinder Singh Kapany ((31 October 1926 – 4 December 2020) Indian-American physicist who is widely acknowledged as the father of fibre optics. He coined the term fibre optics for the technology transmitting light through fine glass strands in devices from endoscopy to high-capacity telephone lines that has changed the medical, communications and business worlds. While growing up in Dehradun in northern India, a teacher informed him that light only traveled in a straight line. He took this as a challenge and made the study of light his life work, initially at Imperial College, London. On 2 Jan 1954, Nature published his report of successfully transmitting images through fiber optical bundles. The following year he went to the U.S. to teach. In 1960, Optics Technology. He holds over 100 patents.*TIS
1935 Ronald Lewis Graham (born October 31, 1935- Jul 6 2020) is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He has done important work in scheduling theory, computational geometry, Ramsey theory, and quasi-randomness. Graham was also featured in Ripley's Believe It or Not for being not only "one of the world's foremost mathematicians", but also "a highly skilled trampolinist and juggler", and past president of the International Jugglers' Association. He is currently the Chief Scientist at the California Institute for Telecommunications and Information Technology (also known as Cal-(IT)2) and the Irwin and Joan Jacobs Professor in Computer Science and Engineering at the University of California, San Diego. *Wik My current favorite Graham quote is, "An ideal math talk should contain one proof and one joke and they should not be the same."
Graham died of bronchiectasis on July 6, 2020, at the age of 84.
 |
| Ron, his wife Fan Chung, and his friend, Paul Erdos |
2022 Marta Cavallo Bunge (Oct 25,1938 – 25 October 2022) was an Argentine-Canadian mathematician specializing in category theory, and known for her work on synthetic calculus of variations and synthetic differential topology. She was a professor emeritus at McGill University
With her doctoral student Jonathon Funk, Bunge is the co-author of Singular Coverings of Toposes (Lecture Notes in Mathematics 1890, Springer, 2006). With Felipe Gago and Ana María San Luis, Bunge is the co-author of Synthetic Differential Topology (London Mathematical Society Lecture Note Series 448, Cambridge University Press, 2018).
DEATHS |
| *willgater |
1867 William Parsons, 3rd Earl of Rosse (17 Jun 1800, 31 Oct 1867) was an Irish astronomer who built the largest reflecting telescope of the 19th century. He learned to polish metal mirrors (1827) and spent the next few years building a 36-inch telescope. He later completed a giant 72-inch telescope (1845) which he named "Leviathan," It remained the largest ever built until decades after his death. He was the first to resolve the spiral shape of objects - previously seen as only clouds - which were much later identified as galaxies independent of our own Milky Way galaxy and millions of light-years away. His first such sighting was made in 1845, and by 1850 he had discovered 13 more. In 1848, he found and named the Crab Nebula (because he thought it resembled a crab), by which name it is still known. *TIS A reproduction of the Leviathan of Parsonstown (now Birr) Ireland at Birr Castle, Rosse’s ancestral home and is open to tourists.
1899
Juliusz Paweł Schauder (September 21, 1899, Lwów, Austria-Hungary – October, 1943, Lwów, Occupied Poland) was a Polish mathematician of Jewish origin, known for his work in functional analysis, partial differential equations and mathematical physics.
He had to fight in World War I right after his graduation from school. He was captured and imprisoned in Italy. He entered the university in Lwów in 1919 and received his doctorate in 1923. He got no appointment at the university and continued his research while working as teacher at a secondary school. Due to his outstanding results, he obtained a scholarship in 1932 that allowed him to spend several years in Leipzig and, especially, Paris. In Paris he started a very successful collaboration with Jean Leray. Around 1935 Schauder obtained the position of a senior assistant in the University of Lwów.
Schauder was Jewish, and after the invasion of German troops in Lwów it was impossible for him to continue his work. In his letters to Swiss mathematicians, he wrote that he had important new results, but no paper to write them down. He was executed by the Gestapo, probably in October 1943.
Most of his mathematical work belongs to the field of functional analysis, being part of a large Polish group of mathematicians, i.e. Lwów School of Mathematics. They were pioneers in this area with wide applications in all parts of modern analysis. Schauder is best known for the Schauder fixed point theorem which is a major tool to prove the existence of solutions in various problems, the Schauder bases (a generalization of an orthonormal basis from Hilbert spaces to Banach spaces), and the Leray−Schauder principle, a way to establish solutions of partial differential equations from a priori estimates. *Wik
1988 George Eugene Uhlenbeck (6 Dec 1900, 31 Oct 1988) Dutch-American physicist who, with Samuel A. Goudsmit, proposed the concept of electron spin (Jan 1925) - a fourth quantum number which was a half integer. This provided Wolfgang Pauli's anticipated "fourth quantum number." In their experiment, a horizontal beam of silver atoms travelling through a vertical magnetic field was deflected in two directions according to the interaction of their spin (either "up" or "down") with the magnetic field. This was the first demonstration of this quantum effect, and an early confirmation of quantum theory. As well as fundamental work on quantum mechanics, Uhlenbeck worked on atomic structure, the kinetic theory of matter and extended Boltzmann's equation to dense gases.*TIS
Credits
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
Well, you get old and eventually you learn stuff. I got a note from Charles Wells who said, " The *name* Halloween came from the British. It is the eve of All Saints Day (Hallowmas, November 1) which is celebrated all over Catholic Europe, not just in Britain. November 2 is All Souls Day, meaning the day for sinners as well as saints. That is the Day of the Dead in Mexico."
