Calculate/Calculus The origin of both these words is in the Greek word Kalyx, for pebble or small stone. The manipulations of small stones on counting boards to do arithmetic operations led to the present mathematical meanings of calculate and calculus. The pebble root is still present in the medical use of the word calculus, a name for an accretions of mineral salts in the body into a small "stone" such as kidney stones. The name for the element calcium comes from the same root. The prefix calci usually relates to calcium or limestone in some way. The furnace used for annealing in the glass making process is called a calcar, and the same word is used for a spur or projection on the heel. Interestingly, the material created in the calcar (glass furnace) is called frit, and is the root of the food product called a fritter; both words coming from the Latin word for fry, which still shows up if you look for "French Frys" in France!
Calculus in the modern use was created by Leibniz, but Newton preferred "the method of fluxions."
Calculus of variations – A large branch of mathematical analysis that uses functionals (functions of functions) and seeks to find extreme values. Typically these functionals are integrals or derivatives of some unknown functions. Calculus of variations began with Newton and his “minimal resistance problem” but (in my opinion) it really started with the brachistochrone problem (see Brachistochrone for more on this) and the Bernoulli family in the late 1600s. After this problem, Leonhard Euler truly worked on the subject in 1733. Lagrange, highly influenced by Euler, also began working on this and, at 19 years old, Lagrange influenced Euler in fact to the point that Euler stopped his work (which was a geometric approach) and favored Lagrange’s analytic approach and declared the subject “calculus of variations”. After Euler, dozens of mathematicians took to their offices and began contributing. Some include Legendre, Gauss, Poisson, Cauchy, Jacobi, Sarrus, Weierstrass, etc. Lots of different subfields arose as well such as Morse theory, and dynamic programming. *Derek Orr
Calendar comes to us from the name of a bookkeeping ledger, and indirectly from the ancient Roman practice of starting each month on a new moon. In the earliest Roman calendars, as in many early societies, the cycle of social events was based on the moon. The date of the new moon would signal a new month and the first day of the month was called the kalends. Many official practices would occur on this date. The community would gather to hear the announcement of the dates on which the "nones: (nine days before the full moon) and the "ides" (the full moon) would occur, and then, as now, the people to whom you owed money would come round looking for their due. The money lenders of ancient Rome kept their accounts in a record book and it became known as a Kalendarium. Eventually this term was applied to the record of dates that we now call a calendar. The genus of the common Pot Marigold, calendula, is from the same root, seemingly because it was thought to be a cure for menstrual disorders.
Cantor's Diagonal Argument was Georg Cantor's second method of proving that the real numbers are uncountable (they can not be matched in a one-to-one match with the counting integers, and thus that there were two different "sizes" of infinity, one that is countable and one that is not. His first proof had been in 1874, and this one followed in 1891. He said used binary digits, and said that if you thought you had a complete list that was countable, and thus could be ordered 1,2,3.. in a list, then he could make a new number which has a first digit not the one used in the number associated with one, and the second digit not equal to the second digit in the number associated with 2, and continuing in this fashion he would create a number that could not be in your list because it disagreed in at least one digit with every number in your list.
Cardinal Numbers are numbers that express amounts, as opposed to ordinal numbers, which express order, or rank. The term is from the Latin cardin, for stem or hinge. Cardinal today means "most important", or "principle", with other things depending (hinging) on it. The first use appears to have be by R Percival in 1591.
Cardiod The path of a point of a circle as it rolls around the outside of a circle of its same size is sort of heart shaped and thus the term is from the Greek root for heart, kardia. It can also be called an epicycle with one cusp, and also a Conchoid. You can graph your own in polar form with the equation r= 2a(1-cos(t)).
 |
| *Wik |
The term seems to have first been used by Giovanni Salvemini de Castillon (1708-1791)
Carmichael Number is named for Robert Carmichael who actually found the first example of one. They had been defined by A. Korselt in 1899, but are named for Carmichael who found the first example, 561= 3*11*17, in 1910. The interest is in the similarity to Fermat's Little Theorem, which says that if p is any prime number, then for any integer b, it will be true that \( b^p - b\) is an integer multiple of p. Carmichael numbers, are composite numbers so that for any b that is relatively prime to n, then \( b^{n-1} \)is equal to 1 Mod(n) .
Carry (arithmetic) Although the word is now less popular with teachers, the "carry" was once a formal part of every American school child's vocabulary, with its opposite action of "borrowing." D. E. Smith asserts that the popularity of the term is due to Hodder's Arithmetic in 1664.
Today the "carry" is more often labeled as grouping or composing. The name carry most likely came from a similar act in accounting when amounts are "carried" from one column, account, or ledger to another. The early Indo-European root is from kers, for run. The root emerged in Latin with cursus, to run, and carrus, for a two wheeled wagon. Can you see the origin of the modern words carriage, and car? Words like current, cargo, caricature (carried to an extreme) and the modern computer term, cursor(runs before the type) all come from the same source.
Although the topic of "carrying" may seem trivial to some, David Wells points out in "The Penguin Book of Curious and Interesting Mathematics" that carrys play an important part in Hilbert's tenth problem. If we let n be the number of ways that a objects can be chosen from a+b objects, and p be any prime number, Ernest Kummer (1810-1893) showed that the largest power of p that would divide n is p^x, where x is the number of carries when a is added to b in base p. As an example, if we let a=7 and b=15 then then to know the greatest power of 2 that divides 170544 (22 choose 7) , we simply convert 7 and 15 to base 2. We have 111+ 1111 which gives us 10110, the base two number for 22 and the operation requires 4 carrys. That means that 2^4=16 divides 170544 , and no larger power of two will work. And now, as the British say, "Carry On."
Cartesian – Relating to René Descartes (1596 – 1650), most notably used for the Cartesian coordinate system. It was the first link between Euclidean geometry and algebra, geometric shapes could be described by algebraic equations. Descartes published this idea in 1637 in La Géométrie, however this was also independent discovered by Fermat but he did not publish his findings. Both Descartes and Fermat used a single axis in the beginning. Two axes were introduced much later after his text was translated into Latin in 1649.
Hamilton used "Cartesian method of coordinates" in a paper in 1844. Cartesian is used as a modifer for other terms such as Cartesian Geometry ((Jean Bernouli 1692) and Cartesian product (Hausdorff, 1914). *Derek Orr
Casting Out Nines See my "Casting About for the History of Casting Out Nines" An additional note, the act is mentioned in Fibonacci's Liber Abaci, but I did not include that he used the term pensa, for the digital root. *D. E. Smith
Catalan Numbers The numbers in the Catalan sequence answer questions such as the following: In how many paths can you move from the origin of a coordinate axis to the point (2n+2, 0) if each move consists of a diagonal move between two lattice points and you cannot touch the x-axis anywhere between the beginning and ending point of the path, in how many ways may 2N beans be divided into tow containers if one container can never have less than the second. The sequence of answers is given by 1, 2, 5, 14, 42, 132, .... or in general \( f(n) = \frac{1}{n+1}(\binom{2n}{n}) \)
The pattern for the recursive method is interesting:
\( c_0=1\)
\(c_1 = c_0 * c_0 \)
\(c_2=c_1 * c_0 + c_0 * c_1 \)
\(c_3 = c_2*c_0 + c_1*c_1 + c_0*x_2\)
\(c_4 = c_3*c_0+c_2*c_1+c_1*c_2+ c_0*c_3\)
etc.
The function is named for Eugene Charles Catalan of Belgium (1814-1894), although Catalan referred to them as Segner Numbers. The actual problem Catalan was working on was the decomposition regular polygons into triangles, where the n in the equation is two less than the number of sides of the polygon.
Polygon dissections were under earlier studied by Johann Adreas von Segner and Leonhard Euler. Euler had discussed the problem in a letter to Goldbach as early on Sept 4,1751. In the letter he gave a table of the number of polygons for 3 through 10 sides, and conjectured the formula\( \frac{2 * 6 * 10 \dots (4n-10}{2*3*4 \dots (n-1}\). In the same letter he gave a generating function.
Euler communicated the problem to Segner who gave the recurrence formula shown above for the dissection in 1758.
The problem was communicated to Liouville in 1838 by Terquem who asked if Segner's recurrence could be used to prove Euler's product formula. Liouville shared the question with a number of French mathematicians, including his student, Eugene Catalan. He was the first to observe the combinatorial solution (2n choose n) - (2n choose n-1) and also to link the dissections to parenthesized expressions apparently during his exploration of the Towers of Hanoi Problem.. The term "Catalan Number" arose from a publication of Eugene Netto in 1900, who first credited the sequence as "Catalan Numbers." Many people credit the first use to Eric Temple Bell in 1936.
The name seems not to have been applied widely until 1968 when Riordan's Combinatorial Identities used the term.
Before Euler described the sequence in 1751, it had been discovered by Minggantu, a Mongolina mathematician, but his research was not completed until it was published by one of his students in 1774.
One of the interesting problems that is solved by the Catalan sequence, and there are many others, is the Hands Across the table Problem. If n people are seated around a table, in how many ways can they all be simultaneously shaking hands with anothere person at the talbe in such a way that no ones arms cross each other. Of course, it's here because the solution is the Catalan sequence for n-2.
Catenary A catenary curve is the shape that a perfectly uniform chain, or rope, would form when suspended between two points. The word is from the Latin catena, for chain. The name was first applied, in Latin, by Christen Huygens while studying the form of suspended chains. Galileo thought the shape would be a parabola. As can be seen from the image below, near the vertex a catenary and a parabola are very similar, but the catenary rapidly starts to outgrow the parabola. The two shapes are related by another idea. If you roll parabola along a straight line, the focus of the parabola will move along a catenary curve.
You most likely have seen a catenary arch. The famous Gateway Arch in St. Louis, Missouri is a catenary.
The first person to use the word catenary in English, was President Thomas Jefferson in a correspondence on bridge design with Thomas Paine,who authored the two most influential pamphlets at the start of the American Revolution
Ceiling Function/Floor Function Both these terms were created in the same document, K. E. Iverson's A Programming Language in 1962. The idea, in terms of the integer function, dates back to Legendre in 1798.
The ceiling function of x, is the smallest integer, C, that that is greater than x. The floor function is the largest integer F, that is not greater than x. The terms were drawn for the common modern usage of the two terms.
Gauss gave us the first symbol for the integer function, today called the floor function, when he wrote the value of x in brackets, [x] = F. Iverson used the now more current symbols,
for the floor function,
andfor the ceiling function. Census Today a census is a complete enumeration or counting of a population. The Latin root of the word is censere which probably was derived from the Greek cosmos for order. The original meaning was of one who judged, assessed, or estimated the degree of wrong and assessed the penalty (tax) to be paid. It is clear from these combined activities that our word for censor (one who judges the acceptability of materials) and censure (expression of blame or disapproval) are both related. The first attempt at a census (in the current meaning) might well have been the ecclesiastical census of England in 1547. I 1694 an act was passed calling for a complete census of hte English people, but it ws never completed. Up into the 18th century some people objected to the census on religious grounds, protesting their fear that the "Sin of David" would bring God's wrath upon them. (See Sin of David)
Center The word center comes to us from the Greek root, kentrus, for a spur or sharp pointed object. The relation to the center of a circle seems clear. A sharp point was made at a center spot, and a more dull object was dragged around the center to form the circle.
Central Angle In a circle, the central angle is the angle whose vertex is at the center of the circle and the legs as two radii. The term was first used in astronomy in 1761 in reference to an eclipse of the Sun. J A Landau found the use as described above in an 1811 Geometry by John Leslie.
Central angle is also applied to polygons, (generally regular) with a vertex at the center of the circumcircle, and the legs reaching out to consecutive vertices.
 |
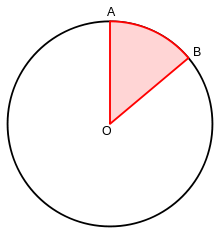| *Wikipedia |
Centroid (or Center of Gravity) The center of gravity in a planer object is the point which would balance the triangle if its mass is equally distributed. There are also centers of gravity considering only equal masses at the vertices, and others for the mass of the sides in uniform density. More complete information in this post. Just an Average Point.
Century Although now used almost exclusively for a period of one hundred years, century was originally the Latin term for any collection of 100 items. In the Roman army a company consisted of one hundred men, and each was called a centurion.
Cevian A word created by French geometers around the end of the 19th century to honor the Italian mathematician Giovanni Ceva. A cevian is a line segment from a vertex of a triangle to a poin ton the opposite side. The median, altitude, and angle bisector are all examples of cevians. The perpendicualr bisector, in most cases, is not a cevian because it does not (necessarily) pass through a vertex. Note that a cevian may cut the opposite side extended outside the triangle.
Chain Rule Although it has been applied in other ways in history, today the term refers to one of the earliest rules in differential calculus. I have a note on my On This Day in Math site that Liebniz struggle to work out the rule, "1675, In a manuscript Leibniz struggled with the product and quotient rules for differentiation. At first he thought d(uv)= du dv. *VFR Cajori writes about the same document that Leibniz first used dx and dy as the differentials of x and y, respectively. It would not be until the 21st that he completes the product rule. *F Cajori, History of Mathematics, (pg 208) ".
The chain ruleto find the derivative for a product of two functions u and v (think of something like x^3(sin(x)) is given by d(uv) = u dv + v du.
Chaos Although the ideas of chaos theory as we know it today have been actively studied at some level for most of the 20th century, the word as a mathematical term dates only from an article in American Mathematical Monthly in 1975 "Period Three Implies Chaos."
The Greek root, khaox, was for an empty space. The meaning still persists in archaic usage where it refers to a canyon or abyss. The evolution of the word to mean disorder seems to come from reference to the time before the creation of the universe. The empty space was without order, and the creation filled the emptiness with order.
A more common form of the word exists today, but few people are aware of the connection. At the start of the 17th century, a Flemish scientist named Jan Baptist van Helmont was studying the bubbles that rise when fruit juice was allowed to stand. These strange vapors, without shape or form, reminded him of the Greek idea of Chaos, so he called them by the Germanic(Flemish is a dialect of German) spelling of chaos, gas. The physical objects formed out of the void wer called the Cosmos, the Greek word for orderly or well formed. Today we hear people refer to the universe as the Cosmos. When Robert Milliken, the American physicist, sought a term for the radiation that seemed to be coming from everywhere in the universe (the cosmos) he suggested the name Cosmic Rays. Today the word cosmos also remains as the roots of words like cosmopolitan, and cosmetics.
Charasteristic (logarithms) See Mantissa
Check When your teacher tells you to "check your work", they may not be thinking of it as a number related word, but between its ancient origins and its multiple meanings of today, check has roots in the history of mathematics. The origin of the word began with the Persian word for king, shah. When the ancient game of chess was played, it was called by this name, because the king ws the most important piece. The Latin derivation of the word became scaccarium, and became exchec in French.The board became a checquered board and cloth which bore this pattern of crossed rows of parallel lines began to be called "check cloth." They were used in counting tables all over Europe and became a formal part of the official procedures of banking in 13th century England. In 1186 the Royal Treasurer of England, Richard, the Bishop of London, wrote dialogus de Scaccario (Dialog about the Chessboard). In it he describes how a "black cloth with parallel lines at equal distances" was placed on the counting board and used in auditing the official records. Official accounts were recorded on tally sticks, and the counting board was used to verify the accuracy. This is where we get the expression, "check your work." The stock of the tally stick was redeemed for money if the tally stick "checked" and provides the source of our word for a negotiable bank instrument called a "check". Eventually the name of the British Royal treasury began to be called the Exchequer. A name for a king becomes the name for the place where the king keeps his money.
Chiliad ˈki-lē-ˌad "What's the difference between a chiliad and a millennium? Not much: both words refer to a period of 1000 years. While millennium is more widely used, chiliad is actually older, first appearing in the late 1500s (millennium didn’t make its way into written English until the following century). Not surprisingly, both words trace back to roots that mean thousand. Millennium comes from the Latin mille, and chiliad is a descendent of the Greek chilioi." *Merriam-Webster
Chiral In chemistry, a molecule or ion is called chiral if it cannot be superposed on its mirror image by any combination of rotations and translations. This geometric property is called chirality. The terms are derived from Ancient Greek χείρ, meaning "hand"; which is the canonical example of an object with this property.
Chi Square The statistical test, and the name for it are both credited to Karl Pearson around the year 1900. The Chi square test, often written as \( \Chi^2 \) is a statistical test of the probable outcome from a population with a Chi square probability distribution It is also used for a Pearson Chi-square test to determine if the actual distribution of some outcomes agree with theoretical expectations to some specific standard. The Chi-square distribution with k degrees of freedom is the sum of the squares of k random normal variables.
 |
| *Wikipedia |
Chord The Greek root of the chord, chorde, means gut or string. The musical use of the term comes from a contraction of accord, two strings played together. Although students first meet the chord as a segment joining two points on a circle, it may be used for the segment connecting two points on any curve. The term is used by Robert Recorde in 1551.
Circle The Latin root of the word circle is circus. The traditional shape of the large roofless enclosures in which the famous Roman chariot races were run was circular, or oblong, and thus the word came to describe this shape as well. The Greek word for circle was kuklou. Circle can be tricky to define for all the ways we use it, Even Euclid seems to have gotten confused. He defines the circle as " a plane figure bounded by one line called its circumference" but later in Proposition I, he treats circles as if they are only their circumferences. The confusion comes from mathematicians wanting to sometimes use only the area inside the circumference, sometimes only the circumference, as when two circles intersect, and sometimes we want them to be the combination of both.
Circumference The Latin roots are circus, the root of circle, with ferre which meant "to carry", thus literally " to carry around.The word is the Latin translation of the Greek word, periphereia with the same meaning. The word was used before Euclid and seemed to have been common in Greek mathematics. According to Jeff Miller's excellent web page on the first use of math words, "Peripheria was used by Heraclitus (who wrote) 'The beginning and end join on the circumference of the circle (kuklou periphereias)". Perhaps it's long history accounts for the fact that the Greek form of the word also persisted in Latin as a borrowed word and made its way into English in words such as peripheral.
Circumcircle/Incircle Every triangle has a circle that passes through the three vertices of the triangle. That circle is called the circumcircle, and its center is called the circumcenter. The Radius is called the circumradius, and usually represented as R, with the lowercase r being reserved for the smaller inradius, which is the radius of the incircle, a circle inside the triangle that is tangent to all three sides of the triangle. The center of the incircle is the
 |
| *Wolfram Alpha |
The circumcenter lies inside the triangle if it is acute, on the hypotenuse of the triangle if it is right, and outside the triangle if it is obtuse. The diameter of the circumcircle is given by the law of signs, it is the ratio of any side to the sine of the opposite angle. The diameter, 2R, can also be found as the product of all three sides divided by twice the area, \(2R= \frac{abc}{2Area}\)
The circumcenter is most often labled O, and the incenter by I. The incenter can be found at the intersection of any two angle bisectors of the triangle.
The radius of the incenter can be found by using Heron's formula for triangles \( \frac{\sqrt(s)(s-a)(s-b)(s-c)}{s} \) where s is the semi-perimeter, half the sum of the three sides. The distance between the two incenters can be found using a relationship that carries Euler's name, but seems to have been discovered earlier by William Chapple in 1746. The distance is often written using the common symbols for the two centers, OI, OI2 = R(r-2r)
Coefficient A coefficient is a number, or variable, that multiplies a variable term. In a common linear equation like 2x - 3y = 5, the 2 and 3 are the coefficients of a variable term. In a typical quadratic equation like A2 + Bx + C = 0, we call the variables A, B, and C the coefficients of the term, even though they are themselves variable quantities, they represent some unknown constant that does not vary in each expression, unlike the x, which varies throughout the evaluation. The origin of he word reaches back to the early Latin word facere, to do. The ex (which slips into ef because of the first letter of the next root) preceding this root gives the meaning of "bringing about" a result, and is the source of the intermediate word effect, and its variation efficient. We add co, the root for with, to form coefficient. The math historian F. Cajori credits 16th century mathematician Francois Vieta for the creation of this word, but suggests that it did not become common until near the beginning of the 18th century.
collinear Two or more points are said to be collinear if they lie on the same line. The roots are easy to identify as the Latin con or com for with, and the root linear for line. The double letter where the last letter in the prefix is changed to match the first letter of the root word, just as the double f was formed in coefficient. Here is a comment on this practice from John H Conway that was posted to a discussion group:
The "co" here is from the Latin "con", meaning "with". Such Latin prefixes have a habit of merging with the next consonent in certain circumstances. For instance the "in ", meaning "not" has done this in words like "irreparable" and "Immiscible" which should logically be "inreparable" and "inmiscible", which would be much harder to pronounce, as would "colinear". There are lots of other examples, most of which are so familiar that one no longer analyses them- for instance"offer" should logically be "obfer", meaning (roughly) "to bring out", and "differ", which should be "disfer" (to bring apart) ... and so on.
Combinations Combinations tell the number of ways of selecting a group of k things from n items. For instance if you wonder how many ways are there to select two letters from the English alphabet of 26 letters, you would be asking the mathematical question, how many ways can we select 2 distinct things from 26 things. Note that the definition rejects picking aa, or bb or any other repetition of the same letter, and does not distinguish ab from ba. If order is important you are dealing with an issue of permutations.
The formula for the number of ways that k distinct things can be selected froma group of n things is \( (\binom {n}{k})=\frac {n(n-1)\dotsb (n-k+1)}{k(k-1)\dotsb 1}\), The word was used with its present meaning by John Wallis and Blaise Pascal.
Compact (space) – generalization of being closed and bounded. Sequentially, compact means that every sequence that lives in some space has a convergent subsequence and the subsequence converges in that space. Topologically, it means that every open cover has a finite subcover. In the 19th century, Bernard Bolzano knew that every bounded sequence has a convergent subsequence, dealing with limit points. Weierstrass would then rediscover this nearly 50 years later. In the 1880s, a significant finding was the Bolzano-Weierstrass theorem held for sequences of functions as well as points. This was very peculiar…to think of a function as a point object, which also gave way to looking at function spaces. Arzelà and Ascoli were some of the first ones to study function spaces and they came up with the Arzelà-Ascoli theorem which generalized Bolzano-Weierstrass. In the early 20th century, Arzelà and Ascoli’s findings starting appearing in integral equations under the work of Hilbert and Schmidt. This then led to compact operators and compact spaces. It was Maurice Fréchet who coined the term “compactness” as the Bolzano-Weierstrass property and used it in this 1904 paper as well as his 1906 thesis.
However, there was another since of the word in the late 1800s. In 1870 Eduard Heine proved that a continuous function on a closed and bounded interval was uniformly continuous. In the proof, he shows that any countable cover of the interval can be shortened down to a finite collection of covers and can still fully cover the interval. The significance of this lemma was recognized in 1895 by Borel and it was generalized to arbitrary collections by Pierre Cousin and Henri Lebesgue. And then, the Heine-Borel theorem was born. This was very significant since it used local information to prove a global property about a function. In 1904, Lebesgue took advantage of this when he formulated what is now the Lebesgue integral. Pavel Alexandrov and Pavel Urysohn formulated Heine-Borel compactness in a way that could be applied to topological spaces. In 1929, they also showed that the compactness from Fréchet (sequential compactness) followed from topological compactness. *Derek Orr
Compass Many students wonder why the name of the instruments used to draw circles, and the name of the navigational aide used to find directions share a common name. The origin of both words is from the use of a compass to mark off length. The Latin word passus means step, and a compass was used to mark off equal steps. . Later the French extended the meaning to include any act of measuring off by steps. For navigation, these steps were often around a circle used to measure the direction from North, and the object used to measure was the magnetic needle, and a floating card that marked off equal steps around a circle, called a compass card. Eventually the card, needle, and all were addressed with the single word, compass. The English extended the idea to other circular references, and then to a general idea of inclusion or surrounding with words like encompass, and compassion.
Complementary The Latin word complere means to complete. The ple root is the same root that gives us the word plus. Most mathematical uses of complement can be understand from this origin. A complement to an angle is the amount need to complete a right angle. The "tens compliment" of six is four, the amount needed to complete a ten. The word compliment, for an expression of praise or admiration, is from the same root. It came from the Spanish for the gift that would repay someone for a favor. The gift that would complete the exchange.
The earliest use of complementary angle I found in a Google search was in 1851, First book on Plane Trigonometry by George W Hemming.
Complex Numbers The use of the word complex for a number of the form a+bi, where i= \( \sqrt{-1} \) was introduced by Karl F Gauss around 1830. Gauss wanted to distinguish between the imaginary part, bi, and the sum of the real and imaginary part and used the phrase "numeros integros complexos". The first use of the term in English seems to have happened about 25 years later in a paper by Sir William R Hamilton.
Component When students first study vectors they think of the component parts primarily in terms of the horizontal and vertical components of the vector, but really the components in that since are the tow unit vectors i=(1,0) and j= (0,1); but any two vectors that can be added to make a third are the components of the final vector. This word also begins with the Latin root com for with and joins it to ponere, to place. Literally then, the components of the vector are the vectors that are "placed together" to form the resultant. Other math words from the same bases include compound and exponent.
Composite and Compound A composite number is one that is a product of other parts, its factors. The word joins the Latin com (with) and ponere (to put) to make "to put together". Compound is drawn from the same roots and has the same meaning. A compound number is a number with a whole part and a fractional part put together. A composition is so called because it is the putting together of parts or elements to make a whole. Compost in the garden is a mixture of decaying organic matter, and a compote is a fruit cooked in heavy syrup until the fruit and syrup are mixed. You can probably think of many others, compose, composition...
Compound fractions are those which are greater than one, and thus combine a whole number part with a fractional part, \$ 3 \frac{1}{4} \$ for example. Fractions greater than one written with a larger numerator than the denominator are called improper, but are perfectly acceptable to use anyway.
Compute joins the com(with) and the Latin root putare. This root is often cited as related to thinking or reckoning, but its meaning comes from an early word for cut or slice. The same root appears in amputate. This goes back to the earliest use of numbers in commerce and the idea of comparing values to a counting or tally stick. The sticks were notched to record values for future reference. Computing, then, was comparing the quantity of items to the marks on the tally stick. This helps to understand the word dispute. Dis is from the root duis for two, and is used to represent the idea of two things separated. If one is disgraced, they are separated from grace. Dispute literally means " a separate or different count.". A difference in the records could easily lead to what we now think of a s dispute.
Concantenate comes from the same Latin root that gives us the Catanery arch, catena, for chain. It literally means to link things together like a chain. Compound words like snowball are concatenations of the words snow and ball. In math we sometimes use the term to describe writing a group of integers into a single number. The concatenation of the first three primes, 2, 3, and 7, is the number 237. We could concatenate the first six odd numbers to get 1357911.
Concurrent Although concurrent is used in common English to mean things that happen at the same time, the mathematical relationship is more about the same point in space rather than in time. Two or more lines are concurrent if they all pass through a common point. This idea of "running together' is the basic idea behind the word concurrent. The con is the common prefix that means with or together, and current is from currere which meant "to run". A currier is one who runs messages from one point to another. Current, course, and currency(as in money) are also from the same root as is the little flickering line or mark that moves ahead of the type on your computer screen, the cursor.
Conchoid A conchoid is a curve derived from a fixed point O, another curve, and a length d. It was invented by the ancient Greek mathematician Nicomedes. The simplest expression uses polar coordinates with O at the origin. If
expresses the given curve, then
expresses the conchoid.
Cone seems to come to us almost unchanged, in form or usage, from its early Greek roots. Knonos was the Greek word for a pine cone. It is probably related to an earlier proto Indo-European root ko, ke that related to sharpening. Objects having been sharpened to a point like the tip of a cone. A cone is formed by the motion of a line with one point fixed and the other following along the perimeter of some plane closed curve. Although most commonly using a circle, it is not the only such shape. Mathematically the cone is considered to extend both ways as the line is treated as infinitely long. If you imagine two ice cream cones with the points together, you get the picture. The two surfaces on each side of the central point are called the two nappes of the cone, from the French word for a sheet or a cloth. You all know at least one word derived from that. The French root actually seems to go back to the Latin for a map.
Conic If a plane is passed through a circular cone the resulting trace of the cone is called a conic section, such as the circle, ellipse, hyperbola and parabola.
Congruent The Greek word congruent meant "coming together" or "working together". Whether applied to a geometric shape or a military unit, it meant that the parts fit together perfectly. Two Triangles ABC and DEF are generally shown to be congruent by using the equivalence, or congruence symbol, ABC \(\equiv \) DEF.
Conjecture A mathematical conjecture is a tentative conclusion in the absence of formal proof. We think it is so, but have not, or can not prove it. After looking at the three altitudes in dozens of triangles, and observing that in each case they intersect at a single point, a student may make the conjecture that this happens in all triangles. His repeated examinations give her reason to believe the statement may be true, but not sufficient evidence to declare the statement proven. The word seems not to have been common until the beginning of the 20th century. The prefix is the often used com, for with or together, and the principle root from jacere, to throw. When we make a conjecture we throw two ideas together, the hypothesis and conclusion, before the relationship is fully tested.
Conjugate is the union of the common Latin prefix com (together) and the root juge (yoke) and means to bind together in a pair. Mathematically it is often used for things that are opposites in some way, as in the complex conjugates, with equal real parts, as opposite imaginary parts. (a + bi, a - bi). In this case, the conjugates yoked together through multiplication produce a real number, a^2 + b^2.
The same word in grammar refers to words of a common origin and related meanings, like the various conjugations of "to be", am, are, is; and in biology it refers to an act of sexual union, for which the more common term is conjugal relations.
Couture Lines See Isogonal Lines
Constant The mathematician uses the word constant to represent an unchanging or fixed quantity. Often the quantity is unknown, and is thus represented by a symbolic value such as the use of b in y= mx + b to represent the value of the y-intercept, which may change from line to line, but is constant in any one of them. This use of constant/variable seems to be a contradiction to students at times. I have sometimes opted for the term "pronumeral" , derived from the idea of a pronoun such as "she" when it stands for a specific person, but the person is not identified. In the same way f(n) = 4n+3, uses the n as a variable, it can take on many values; but in 15=4n+3, the n is a pronumeral. We may not know, or have to figure out what number is being spoken of, but there is (in this case, only one).
Contact Triangle is another name for the triangle connecting the points where the incircle is tangent to a triangle. It is often called the intouch triangle and the Gergonne triangle. The contact triangle is the Pedal (foot) triangle of the incircle with respect to the incenter, which is a way to say it joins the three points where a line perpendicular to a side passes through the incenter.
Continuous The mathematical creation of continuous is credited to Leonhard Euler in his "Introduction to Infinite Analysis". For the beginning student, it is easy to think of a continuous curve or line as one that can be drawn completely without picking up the pencil; that is, one with no jumps or breaks in the curve. Of course the flaw to such a pattern is imagining the real number line with all the irrationals removed. The "holes" that would exist from the removal of them, being without measure, could not be noticed in pencil line. Some early types of lines students meet that are not continuous would by step functions, and functions with more than one vertical asymptote such as the tangent function. The prefix is the common Latin com for with. The main root tingere, touch or pull is from the same that gives us tension and tangent. The word contingent, for something that is related to the situation is from teh same root and literally means "touching on all sides."
Contour - mid 17th century: from French, from Italian contorno, from contornare ‘draw in outline’, from con- ‘together’ + tornare ‘to turn’. It appears in “contour integration”, a method of evaluating integrals by integrating along a line in the complex plane. Also “contour line” is a line where a function is constant. Contour lines often begin with “iso-’’ meaning “equal” in Greek See Also Isogonal *Derek Orr
Convergence – From late Latin meaning “inclining together”. It means when some mathematical list of objects (sequence of numbers/functions, partial sums, etc) approaches a well-defined quantity as some variable increases or decreases to another well-defined quantity. Divergence is just the opposite; the list of objects does not approach a well-defined quantity. Sometimes if the limit of this list is infinite, some will say the list “converges to infinity”.
Gauss developed certain convergence criteria for simple hypergeometric series in 1812 after Euler worked with them. Cauchy in 1821 pushed for stricter series convergence tests after discovering that two series can converge but their product can diverge. Cauchy expanded the notion of a power series as well as its convergence criterion by looking at complex functions. Abel in 1826 corrected some of his findings by investigating the binomial series for complex variables.
Cauchy’s methods led to special convergence tests (cf. Raabe 1832 and many others). General convergence tests came on with Kummer in 1835 until Pringsheim in 1889 published the most complete general theory.
Uniform convergence was also first thought of by Cauchy but the first to successfully tackle it were Seidel and Stokes (1847,1848). Conditional convergence was studied by Poisson in 1823 who gave the general form for the Maclaurin remainder. Later, Jacobi in 1834 improved this remainder formula.
Cauchy and Dirichlet studied convergence for Fourier series around 1826 and 1829. Dirichlet’s work was later improved by Riemann and many others in the math community.
The OED credits Isaac Toddhunter with the earliest use of convergent in a mathematical sense in hia 1858 Algebra for Schools. *Derek Orr
Converse is from the Latin roots com (great or intense) with vertere (to turn), suggesting the meaning "to turn away." The verb converse (as in conversation), which has the same spelling, is from a completely different root. In mathematics, the converse of a theorem interchanges the properties in the given and the conclusion. If we have a theorem that says "If two sides of a triangle are equal in measure, then the opposite angles will also be equal in measure" . The converse of the theorem would say "If the opposite angles of a triangle are equal in measure, then the two opposite sides are equal in measure." When both the theorem and the converse are true, we often write them together in a single statement, "Two sides of a triangle are equal in measure, if, and only if the opposite angles are also equal in measure" Sometimes the expression, If, and only if, is replaced with the symbol IFF.
Convex comes from the two Latin roots com (with) and vehere (to carry) and literally means to bring (carry) together. The word seems to be a variation of "convection" from the same roots. Vehere is also the base root in vector, and of course, vehicle. In addition the words wiggle, weight, wagon, wave and (this is no joke) wacko are all related back to the common root.
Corollary The mathematical use of corollary is to describe a proposition that can be shown to be true with little or no effort from some theorem already proven. We would say this theorem is a corollary of that known theorem. It is sometimes also applied to the results of deductive and inferential reasoning but more generally as the consequence or result of something else. The root is found in the Greek word for curved, Koronos. Variations of hte word produced corona in Latn, for crown, which has been in the news later with a new corona virus outbreak. The diminutive of corona is corolla for a garland or little crown. This last term was used to describe a small sum of money that was passed as a gratuity, what we would call a tip today.
"Well, where does this get into the math?" you ask. The incredibly prolific Euler would prove theorems so quickly and write them up ignoring the little association truths they revealed, perhaps because he thought they would be obvious. Editors of his work would insert little notes of these other proofs in the margin of his papers, and mark them with a little garland, or corollary, as if to honor the theorems which made them clear. It is from this source that we come to call these secondary results corollaries of the original proof.
Correct Our word for something that is error free is through the French, but from the Latin correctus, which joins the com (with) prefix with the root regere (to make straight) the rect is the same root as in rectangle, and erect. Many reg words and rect words refer back ultimately to regents, or rules, and the right angle, and right itself fall back to this source.
Correlation The long road to the long word correlation begins with the ancient Sanskrit word for scales, tula. The action of a scale to life=t or support the weight let to the Greek word telamon for one who supports or bears something.This flows into the Latin word latus for "side", Finally the co root is added to indicate that something the same of shared. Two things on the same side or related to a common thing. In statistics the coefficient of correlation is the degree to which the elements of two sets are related to each other in an ordinal way. It may be by chance, or a cause, but they "move together".
Cosine,Cotangent, and Cosecant The consine functon was created to describe the sine of the complimentary angle, and hence its name. The Hindu mathematician Aryabhata (475-550) called it Kotijiva, extending the term for sin, jiva. One of the first to use abbreviations for trigonometric names was Thomas Finck, who wrote sin.com. and tan. com. around 1583. He is also the person who created the terms tangent and secant. The English began using abbreviations later, and without dots. Edmund Gunter created the "co.sinus" and "co.tangens" and John Newton modified the one to "cosinus" in 1660. William Oughtred used t for tangent, and t co for cotangent. John Wallis used T and t for tangent and cotangent. By 1748 Euler used cos., and then a year later without the period.
Cosines, Law of Although the word cosine had not been created yet, Euclid's Elements has two postulates (Book 2, Postulates12 and 13) which essentially are the Law of Cosines written in geometric rather than algebraic form
Proposition 12The Persian mathematician of the 15th century Jamashid al-Kashi provided the first expression of the rule appropriate for later algebraic application, and permitting triangulation. The rule is sometimes named for him in some cultures, including France.
In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle.
— Euclid's Elements, translation by Thomas L. Heath. *Wikipedia
The expansion to the West is usually credited to Viete but it was not until the early 19th century that it progressed into the algebratized and now well known classic.
The law is an extension or generalization of the Pythagorean thm into both obtuse and acute triangles. \(c^2 = a^2 + b^2 - 2abCos(C) \) .
The law is an extension or generalization of the Pythagorean thm into both obtuse and acute triangles. \(c^2 = a^2 + b^2 - 2abCos(C) \) .
There is also a Law of cosines for both spherical and hyperbolic geometry.
Cosmos See Chaos
Cosmic Rays See Chaos
Cramer's Rule named after mathematician Gabriel Cramer (1704 – 1752), it is a way to solve a matrix equation Ax = b by taking determinants involving A and b. Because of the many determinants, it is not computationally efficient unless A is only a 2x2 or 3x3 matrix. Cramer published his result in 1750 although Maclaurin knew of some special cases in 1748 and it is believed he knew about the rule in 1729. Even though Maclaurin had some previous history with this, it is regarded as truly “Cramer’s” rule. It is one of the few rules that are named after the actual discoverer (unlike L’Hopital’s rule, for example).
To save great amounts of writing, I have two images to show the method for a system of two equations in two unknowns which was presented very clearly on the Wikipedia Page:
 |
| *Wikipedia |
Critical Points The critical Points of a function generally refer to the points where the function has a minimum, a maximum, or an inflection point. Sometimes the word is generalized to an "important" point, which often include the zeros, points of discontinuity, etc.
The first use of "critical point" with this meaning was by Edwin Bidwell Wilson in his 1912 "Advanced Calculus", in which he defined them as the points where f'(x) = 0, which would only be local maxima and minima of continuous sections of the curve.
The word comes from the Greek kritikos, to discern or distinguish.
Cube is now the common name for a regular polyhedron with six faces. The cube is one of the five Platonic solids. The word was used by the early Greek geometers, but not always in the way we restrict it now. Euclid used cube in the modern sense, but Heron (Hero) used the term for any right parallelepiped (box shape - what we now call a rectangular prism) and used hexahedron for what we would now call a cube, reversing the modern use of the two terms. The Greek root kubos from which the term is drawn, was from the Greek name for dice used to play games of chance as well as by oracles to divinate the future (in truth, the very early nice were often not exactly either of the two shapes. (see dice) The earlier Indo-European root, keu, which relates to bending, rolling or turning. This can be seen in other words from the same root such as incubate(to lie down on) and concubine, (to lie down with), and left its name in the unit of measure, cubit.
Cubic measure is used as early as 1660 by Robert Boyle, but has shared the field with several other common terms for "solid measure", for example, The Most General School Assistant of 1770 included " 27 solid feet make a solid yard". It also measured 10 cubic feet as a hogshead, with 4 hogsheads to a ton which was 40 cubic feet.
Cumulant – cumulate “gather into a heap or mass”. Cumulants are variants of moments of a function. Cumulants were first introduced by Thorvald Thiele in 1889 who called them “semi-invariants”. They weren’t called “cumulants” until 1932 in a paper by Ronald Fisher and John Wishart. It is said that the name “cumulant” was suggested to Fisher by Harold Hotelling; in 1929, Fisher called them “cumulative moment functions”. *Derek Orr
Cumulative/Accumulate The words both refer to the grouping together of other objects or sets , and both come from the ancient Indo-European root kou from which we also get words like cave, cage, cavity, and excavate. By the time the Romans adopted cumulare for a heap or collection of objects the meaning had apparently extended to the pile made in creating a cave or cavity. Today cumulative often refers to successive additions as in the statistical use of cumulative functions, while accumulate often suggest collecting all at once. A cumulus cloud is so called because it looks like a heaped mass, a pile of cloud.
Curtate and Prolate cycloid The path made by a point fixed on a rolling circle to a point in the interior of the circle generates a curtate cycloid. Curtate is formed from the Latin root curtus, for short. The same root is found in words curt (rudely brief), and curtail (to cut short). If the point is fixed exterior to the circle, it is called a prolate circle. Prolate is little changed from the Latin Prolatus, from the root latus, for side and indicates something that is stretched out.
Both types of curves have the same equation in parametric form, x(t) = rt-h sin(t) , y= r=h cos(t).
 |
| *Wolfram Alpha |
Curve - from Latin curvare ‘to bend’, from curvus ‘bent’. A curve is a line which does not need to be straight, or rather, it is the trace left by a moving point. Over 2000 years ago, curves were seen as decorative and art rather than mathematical. The phrases “straight line” and “right line” are the terms that distinguished “lines” from “curved lines”. In Book 1 of Euclid’s Elements, a line is a “breadthless length” while a straight line is a “line that lies evenly with the points on itself”. The OED's earliest citation for the use of curve in relation to geometry in English was in 1658 by John Collins in a work on use of the quadrant, "to draw the curve...". *Derek Orr
Cusp The word cusp comes from the Latin cuspus and was used to mean sharp or pointed. The points of a crescent moon are called its cusps, and the sharp pre-molar teeth of children are called bicuspids for their two points. In mathematics, a cusp is a point on a curve where two branches meet to have a common tangent line.
The figure at the left shows a traditional "pointed" cusp. Some mathematicians refer to figures like the one at right as a cusp also, the vertical line is tangent to both branches of the curve, but I find that an unsatisfying term. The curve on the left is called a first order or keratoid cusp, from the Greek keras, for horn. If the two branches of the curve both approach the tangent from the same side it is called a ramphoid (bottom image) (from the Greek for bird beak) or second order cusp.
Cycle/Cyclic – from the Greek kuklos, for circle, Or “turn”, is a rotation of 360 degrees or 2π radians. In 1697, David Gregory used π/ρ (rho) as the ratio of circumference to the radius. 50 years earlier however, William Oughtred used δ/π as the ratio of diameter to perimeter (circumference). The first use of π as circumference/diameter was in 1706 by William Jones. In 1737, Euler adapted it which brought it to the public. The use in mathematics was surely influenced by the use of cycles and epi-cycles in astronomy, and the OED gives a citation of R. Braithwaite in Whimzies (1631), "Horizons, Hemispheres, Epicycles are his usual dialect." Terms like "cyloid" (cycle-like), a creation of Galileo in 15991600 indicate that the idea of a cycle as a common usage in science could be generalized without explanation. New mathematical uses of the word continue to appear, Cayley used "cyclical group" in 1891 in the Quarterly Journal of Mathematics, and the studies of Fractals, Dynamics and Chaos in the late 20th century made frequent use of the cycles or orbits of deterministic non-linear sequences that enter into a repeating cycle, such as the unsolved 3n+1 problem. In graph theory a cycle is a closed walk around the vertices, or edges of a graph. A cyclic polynomial is a polynomial which can be circumscribed with a circle containing all the polygons vertices on its perimeter. *Derek Orr
Cycloid A cycloid is the path of a point on the circumference of a circle as it rolls along a straight line. It was apparently named by
The parametric equations of a cycloid of a circle with radius r and with initial cusp on the origin is given by x(t)=r(t-sin(t)) and y(t)= r(1-cos(t)).
The cycloid gained the attention, and interest, of Mersenne, perhaps through his communication with Galileo. Mersenne circulated questions about it among other mathematicians. One of the mathematicians whose attention he brought to the cycloid was the young Giles de Roberval. Roberval used the term term trochiod from the Greek "wheel like". Roberval was able to prove several new theorems ab out the area and tangents of the curve, but did not publish his work.
His choice not to publish was probably because of the method of appointing positions, or chairs, at universities by competitive examination. Roberval's appointment to the "Chair of Ramus" was from just such a competitive appointment, which he had to recapture every three years. Fortunately, the incumbent was allowed to pose the questions for each new competition.
The lack of sharing of information lead to duplication and repetition of efforts, and the bickering that subsequently followed over who discovered what. This was so common in the early 17th century, particularly over the question related to the cycloid, that the curve was nicknamed the Helen of Geometers, a reference to the fighting over Troy for Helen of Troy.
Another interesting story about the cycloid, and another name for it, are related to Blaise Pascal. On the evening of Nov 23, 1954 Pascal experienced what he called a "religious ecstasy" , and subsequently abandoned the study of math and science. Several years later, however, he was unable to sleep as the result of a toothache. Trying to distract himself, he began to study the properties of the cycloid, which he clled by the French word roulette, from the diminutive of the Latin rota for wheel (now you know the root of wheel in two different classic languages). The pain mysteriously vanished, and Pascal took that as a sign that his study of mathematics wsa not displeasing to God, so he returned to writing about math for about another year shortly before his untimely death. The roulette wheel used in casinos is drawn from the same root, so addition of the word "wheel" is redundant.
The area under under a single arch of the curve is equal to three times the area of the generating circle, and the length of the perimeter of a square which would just contain the generating circle. (see Curtate cyloid and Prolate cycloid)
Cylinder is the mathematical term for a surface generated by the locus of lines parallel to a given line, the generatrix, and passing through a curve in a plane, the directrix. In the most common case the curve is a circle, although it could be any closed curve. You could speak of elliptic cylinders or even square cylinders, although we usually apply the term curve to non-polygonal shapes, and use prism for those. The root of cylinder is from the Greek kulindros for roll or revolve. 
No comments:
Post a Comment