On This Day in Math - June 30

You know we all became mathematicians for the same reason: 

we were lazy. 

Max Rosenlicht

The 181st day of the year; 181 is the 9th palindromic prime number.

1f you square 181 and add 7, you get 32768.  So what? Well 32768 is 2¹⁵.  STILL not impressed?  The only other numbers for which n² + 7 is a power of 2 are 1, 3, 5, and 11.... full stop.  And to take this beyond the coincidental, if you replace the 7 with any other integer, there will never be more than two solutions.

and the 181-digit palindromic number made up of all 7's except for the center being 181 (7777...7718177...77777) is a palindromic prime with a palindromic prime decimal length.

181 is the both the difference and the sum of consecutive squares:
\( 181 = 91^2 – 90^2 = 9^2 + 10^2 \)

 Every natural number greater than 181 can be written as sum of cubes of the first two primes. (students might be asked to find all examples of numbers less than 181 that can be written in this fashion, such as 35= 2³ + 3³)

More Math Facts for every year day here.

---

EVENTS

1601.  Johannes Kepler  uses a camera obscura of his own design set up in a tent to view solar eclipses in Graz on 30 June 1601 . Infamously whilst he was busy observing the solar eclipse on the market place in Graz  a thief stole his purse with thirty silver florins. It was Kepler that coined the name camera obscura. The earliest use of the term "camera obscura" is found in his 1604 book, Ad Vitellionem Paralipomena.*RMAT Art Historian J V Field has suggested that in the same book he invented two other math/science ideas: "The two inventions in question are the point at infinity’ and the retinal image. The first is apparently merely mathematical whereas the second is certainly conceived as having physical existence, but the two processes of invention are both closely bound up with Kepler’s conception of the role of mathematical reasoning in natural philosophy, and they consequently have much in common. "

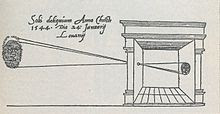Camera Obscura design of Gemma Frisius,16th C

==============================================================

1668     Prince Cosimo's assistant Bassetti writes to  Samuel Morlands agent for his arithmetic machines to request the purchase of one.  "The Prince has heard that a man named Samuel Morland,.., has invented an instrument that is similar to a box of occhiali (glass lenses) which is made in such a way that when you round some circles it is possible to see immediately  the result of some reasoning or mathematical calculation. If this is true, the Prince wants one of those."    

A calculator was sent for the advertised English price of three pounds , ten shillings.  It may be that Morland actually reconfigured his calculator from pounds,shillings,pence to base four scudo.  It is not clear if this Morland-type machine was a gift from Morland, or an Italian made machine copying Morland's technique.  

---

1686 The Royal Society made the decision to publish De Historia Piscium, a lavishly-illustrated history of fishes by John Ray and Francis Willughby. The books was beautiful, but turned out to be such a poor seller that the Society almost went bankrupt. At one point Edmond Halley's salary could not be paid during the same period when he was trying to get Newton to complete his epic masterpiece, The Principia. Fortunately for science, Halley accepted a deal for something like one-hundred copies of the fish book, and then mostly funded the publication of Newton's classic himself over the next year. I don't know if Halley ever managed to sell any of the De Historia Piscium that he took in lieu of salary. *PB old notes.

---

1737 John Harrison, after positive results on the test of his first sea-clock, receives the first money awarded by the Board of Longitude (23 years after the Act to create the Board). Harrison received 500 Pounds, 250 Pounds to be paid immediately, and another 250 Pounds after completing a second clock that passes testing at sea. *Derek Howse, Britain's Board of Longitude: The Finances 1714-1828

Harrison's H2

---

1742 Euler replied (see June 7 post) in a letter dated 30 June 1742, and reminded Goldbach of an earlier conversation they had ("...so Ew vormals mit mir communicirt haben.."), in which Goldbach remarked his original (and not marginal) conjecture followed from the following statement, “Every even integer greater than 2 can be written as the sum of two primes,” which is thus also a conjecture of Goldbach. In the letter dated 30 June 1742, Euler stated:“Dass ... ein jeder numerus par eine summa duorum primorum sey, halte ich für ein ganz gewisses theorema, ungeachtet ich dasselbe necht demonstriren kann.” ("every even integer is a sum of two primes. I regard this as a completely certain theorem, although I cannot prove it.")*Wik
As of this date, no one else has proved it either. It is one of the oldest open questions in mathematics.
Euler also claimed that prime numbers of the form 4n+ 1 are represented uniquely as a sum of two squares. He also mentions that 641 divides 2³² + 1, thereby disproving Fermat’s claim that all numbers Fermat numbers F(n)= \( 2^{2^n}+1\) are prime. Years later we have not found another which is prime.

---

1812 Congress authorized the President of the US to issue interest bearing Treasury Notes for the first time in history.  The interest was fixed at "five and two-fifths per centum a year."  *Kane, Famous First Facts (students might calculate the present value of a $100 investment on that date compounded to the present)

---

1808 Sir Humphrey Davy announced the discovery of magnesium (Mg), calcium (Ca), strontium (Sr) and barium (Ba) on this day in 1808
Throughout his career Davy isolated several metal elements from their compounds through the process of electrolysis, using a primitive electrical battery called a voltaic pile.
Davy also announced he had separated the element boron. However, working independently, French chemist, Joseph Louis Gay-Lussac had announced* the same accomplishment nine days earlier, on 21 Jun 1808.  *TIS

---

1860 Oxford evolution debate took place at the Oxford University Museum on 30 June 1860, seven months after the publication of Charles Darwin's On the Origin of Species. Several prominent British scientists and philosophers participated, including Thomas Henry Huxley, Bishop Samuel Wilberforce, Benjamin Brodie, Joseph Dalton Hooker and Robert FitzRoy.
The debate is best remembered today for a heated exchange in which Wilberforce supposedly asked Huxley whether it was through his grandfather or his grandmother that he claimed his descent from a monkey. Huxley is said to have replied that he would not be ashamed to have a monkey for his ancestor, but he would be ashamed to be connected with a man who used his great gifts to obscure the truth *Wik

---

1894 Tower Bridge opens, In 1886, the foundation stone of the Tower Bridge in London, England was laid (over a time capsule) by the Prince of Wales. The need to cross the River Thames at this point had become increasingly urgent for many years, and finally the necessary Act was passed in 1885. The bridge, designed by Mr. Wolfe Barry, CB, was completed at a cost of about £1,000,000. To permit the passage of tall ships between the towers, two bascule spans, each of 100-ft length, are raised. The side spans to the towers are of the more familiar suspension type. Pedestrians can traverse a high-level footway nearly at the top of the towers, even when the bridge is raised. It was officially opened 30 Jun 1894, by the Prince of Wales, later Edward VII, on behalf of Queen *TIS

---

1905 Albert Einstein's paper, "On the electrodynamics of moving bodies" (special relativity) is received at the Journal Annalen der Physik.
"Einstein develops the special theory of relativity in this paper. His concern, as he makes clear in the introduction, is that then current electrodynamics harbors a state of rest, the ether state of rest, and the theory gives very different accounts of electrodynamic processes at rest or moving in the ether. But experiments in electrodynamics and optic have provided no way to determine which is the ether state of rest of all inertial state of motion. Einstein shows that Maxwell-Lorentz electrodynamics has in fact always obeyed a principle of relativity of inertial motion. We just failed to notice it since we tacitly thought that space and time had Newtonian properties, not those of special relativity. " *John D Norton, Einstein, 1905, Pitt.edu

---

1908 A Comet(?) explodes above Tunguska, Siberia. *VFR In 1908, at around 7:15 am, northwest of Lake Baikal, Russia, a huge fireball nearly as bright as the Sun was seen crossing the sky. Minutes later, there was a huge flash and a shock wave felt up to 650 km (400 mi) away. Over Tunguska, a meteorite over 50-m diameter, travelling at over 25 km per second (60,000 mph) penetrated Earth's atmosphere, heated to about 10,000 ºC and detonated 6 to10 km above the ground. The blast released the energy of 10-50 Megatons of TNT, destroying 2,200 sq km of forest leaving no trace of life. The Tunguska rock came out of the Taurid Meteor storm that crosses Earth's orbit twice a year. The first scientific expedition for which records survive was made by Russian mineralogist Leonid Kulik in 1927. *TIS

---

1945 The first distribution of John von Neumann's First Draft of a Report on the EDVAC, containing the first published description of the logical design of a computer with stored-program and instruction data stored in the same address space within the memory (von Neumann architecture)*Wik

---

1946 ENIAC formally accepted by the government. See 2 October 1955*VFR

---

1948 Encouraged by Executive Vice President Mervin Kelly, William Shockley returned from wartime assignments in early 1945 to begin organizing a solid-state physics group at Bell Labs. Among other things, this group pursued research on semiconductor replacements for unreliable vacuum tubes and electromechanical switches then used in the Bell Telephone System. That April he conceived a "field-effect" amplifier and switch based on the germanium and silicon technology developed during the war, but it failed to work as intended. A year later theoretical physicist John Bardeen suggested that electrons on the semiconductor surface might be blocking penetration of electric fields into the material, negating any effects. With experimental physicist Walter Brattain, Bardeen began researching the behavior of these "surface states."

On December 16, 1947, their research culminated in the first successful semiconductor amplifier. Bardeen and Brattain applied two closely-spaced gold contacts held in place by a plastic wedge to the surface of a small slab of high-purity germanium. The voltage on one contact modulated the current flowing through the other, amplifying the input signal up to 100 times. On December 23 they demonstrated their device to lab officials - in what Shockley deemed "a magnificent Christmas present."

Named the "transistor" by electrical engineer John Pierce, Bell Labs publicly announced the revolutionary solid-state device at a press conference in New York on June 30, 1948. A spokesman claimed that "it may have far-reaching significance in electronics and electrical communication." Despite its delicate mechanical construction, many thousands of units were produced in a metal cartridge package as the Bell Labs "Type A" transistor.

*CHM

---

1954 Solar eclipse in Britain. The about 3 minutes totality was visible in the Faroes and the southern line was crossing the northernmost Shetland. Many people in England do remember this eclipse and is often mistaken as total for those who saw a large partial eclipse. The eclipse track traveled across Norway, Sweden, Lithuania, Byelorussia, and Russia. *NSEC

---

1955 Sperry Rand formed. In 1955 Sperry acquired Remington Rand and renamed itself Sperry Rand. Acquiring then Eckert-Mauchly Computer Corporation and Engineering Research Associates along with Remington Rand, the company developed the successful UNIVAC computer series and signed a valuable cross-licensing deal with IBM. *Wik

---

1972 The International Time Bureau adds the first leap second to Coordinated Universal Time (UTC). *Wik

---

1973     
A group of scientist boarded a prototype French Concorde airplane to chase a solar eclipse. The eclipse promised a luxurious view if you stood at the right place on the planet: a maximum of 7 minutes and 4 seconds as the moon passed over the Sahara Desert. It would be just 28 seconds short of the longest possible eclipse viewable from Earth; in the preceding several hundred years, there had only been one eclipse longer than this one, and there would not be a longer total solar eclipse until June 2150. Not satisfied with one of the longest eclpises in recent history, the group managed to negotiate a viewing flight on the still in testing Concorde. Closing in at maximum velocity, Concorde would swoop down from the north and intercept the shadow of the moon over northwest Africa. Traveling together at almost the same speed, Concorde would essentially race the solar eclipse across the surface of the planet, giving astronomers an unprecedented opportunity to study the various phenomena made possible by an eclipse. In one flight, Concorde had given astronomers more eclipse observing time than all the previous expeditions last century—generating three articles in Nature and a wealth of new data. *Motherboard

---

2011 Mr Ballew finally hung up his spurs and rode off into the sunset with his sweetheart, Jeannie.

---

2015 A Leap second is added to the clock in the last second before 8pm, so there will be a minute with 61 seconds. Between 1972 and 2012, a leap second has been inserted about every 18 months, on average. However, the spacing is quite irregular and apparently increasing: there were no leap seconds in the seven-year interval between January 1, 1999 and December 31, 2005, but there were nine leap seconds in the eight years 1972–1979. *Wik

---

BIRTHS

1748  Dominique Cassini (30 June 1748 – 18 October 1845)  was a French mathematician and surveyor who worked on his father's map of France.  He was the son of César-François Cassini de Thury and was born at the Paris Observatory. In 1784 he succeeded his father as director of the observatory; but his plans for its restoration and re-equipment were wrecked in 1793 by the animosity of the National Assembly. His position having become intolerable, he resigned on September 6, and was thrown into prison in 1794, but released after seven months. He then withdrew to Thury, where he died fifty-one years later.
He published in 1770 an account of a voyage to America in 1768, undertaken as the commissary of the French Academy of Sciences with a view to testing Pierre Le Roy’s watches at sea. A memoir in which he described the operations superintended by him in 1787 for connecting the observatories of Paris and Greenwich by longitude-determinations appeared in 1791. He visited England for the purposes of the work, and saw William Herschel at Slough. He completed his father’s map of France, which was published by the Academy of Sciences in 1793. It served as the basis for the Atlas National (1791), showing France in departments.
Cassini’s Mémoires pour servir à l’histoire de l’observatoire de Paris (1810) embodied portions of an extensive work, the prospectus of which he had submitted to the Academy of Sciences in 1774. The volume included his Eloges of several academicians, and the autobiography of his great-grandfather, Giovanni Cassini.*Wik

---

1791  Félix Savart (June 30, 1791, Charleville-Mézières, Ardennes – March 16, 1841, Paris) became a professor at Collège de France in 1836 and was the co-originator of the Biot-Savart Law, along with Jean-Baptiste Biot. Together, they worked on the theory of magnetism and electrical currents. Their law was developed about 1820. The Biot-Savart Law relates magnetic fields to the currents which are their sources. Félix Savart also studied acoustics. He developed the Savart wheel which produces sound at specific graduated frequencies using rotating disks.
Félix Savart is the namesake of the unit of measurement for musical intervals, the savart, though it was actually invented by Joseph Sauveur.*Wik

---

1856 Cargill Knott (June 30, 1856 – October 26, 1922) born. He graduated from Edinburgh University and was then an assistant in the Physics department. With Barclay and Fraser he was one of the writers who originally proposed the founding of the EMS. He went to the Imperial University in Tokyo as Professor. He returned to a lectureship in Edinburgh and eventually became a Reader in Applied Mathematics. He became Secretary and Treasurer of the EMS in 1883 and President in 1893 and 1918.*SAU

---

1880 Birthdate of Rudolf Fueter (30 June 1880 in Basel; 9 August 1950 in Brunnen) who worked with functions with non-commutative variables and also in number theory. *SAU

---

DEATHS

1660 William Oughtred, (5 March 1575 – 30 June 1660) inventor of the slide rule (1621) and a staunch royalist, died in a transport of joy on hearing the news of the restoration of Charles II. Augustus De Morgan later remarked, “It should be added, by way of excuse, that he was eighty-six years old.” *VFR an Episcopal minister who invented the earliest form of the slide rule, two identical linear or circular logarithmic scales held together and adjusted by hand. Improvements involving the familiar inner rule with tongue-in-groove linear construction came later. He introduced the familiar multiplication sign x in a 1631 textbook, along with the first use of the abbreviations sin, cos and tan.*TIS

---

1919 John William Strutt 3rd Baron of Rayleigh (of Terling Place)(12 November 1842 – 30 June 1919) was an English physical scientist who made fundamental discoveries in the fields of acoustics and optics that are basic to the theory of wave propagation in fluids. He received the Nobel Prize for Physics in 1904 for his investigations into the densities of the most important gases and his successful isolation of argon, an inert atmospheric gas.*TIS

---

Credits
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia

On This Day in Math - June 29

Jeannie, Happy birthday.

The 180th day of the year; 180 can be formed with the only the first two primes... 180 = 2² x 3² x (2+3) *Prime Curios

180 is the sum of two square numbers: \( 12^2 + 6^2 \). It can also be expressed as either the sum of six consecutive primes: 19 + 23 + 29 + 31 + 37 + 41, or the sum of eight consecutive primes: 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37.

180 is a digitally balanced number, its eight binary digits contain four ones and four zeros, 10110100,  they match up into two sets of balanced zero-one pairs, the first four digits, 1011, aligning perfectly with their digital opposite in the last four 0100. Creating the binary digits for 0, 1, 2, and 3

Beautiful trigonometry, arctan1 + arctan2 + arctan3 = pi/2 =180<sup>o

The digits 180 are the only digits in a 15,601 digit prime that is both a palindrome and strobogrammitic. *@fermatslibrary</sup> 

More Math Facts for every year day here.

---

EVENTS

In 3123 BC, a Sumerian astronomer saw a devastating asteroid, perhaps a half-mile wide, according to an interpretation of a clay tablet, made by researchers from Bristol University, reported in The Times on 31 Mar 2008. The ancient date was indicated by a computer recreation of the night sky using symbols on the tablet recording the positions of constellations The Planiform tablet found by Henry Layard at Nineveh, likely a 700 BC copy of the astronomer's notes, described in cuneiform a "white stone bowl approaching" that "vigorously swept along." The asteroid probably crashed into the Austrian Alps, leaving a swath of cataclysmic damage such as, for example, the Genesis destruction of Sodom and Gomorrah.*TIS

Planisphere tablet, British Museum

---

1456 According to one story that first appeared in a 1475 posthumous biography and was subsequently embellished and popularized by Pierre-Simon Laplace, Callixtus III excommunicated the 1456 apparition of Halley's Comet, believing it to be an ill omen for the Christian defenders of Belgrade from the besieging armies of the Ottoman Empire. No known primary source supports the authenticity of this account. The 29 June 1456 papal bull of Callixtus III calling for a public prayer for the success of the crusade, makes no mention of the comet. By 6 August, when the Turkish siege was broken the comet had not been visible in either Europe or Turkey for several weeks. *Wik

---

(John Francis Rigaud, 1785)*Wik

1785 Letitia Ann Sage became the first British woman to fly. From St George's Fields on the south side of the Thames, Vincenzo Lunardi and his partner Biggin, with two invitees, Mrs. Sage and a Colonel Hastings were supposed to make the flight, but the Hydrogen balloon wouldn't take off because of the weight. (Mrs Sage, a actress and model was also a somewhat large woman, rumored to weigh appx 200 pounds.)  Lunardi and Hastings stepped down, and the balloon took off with Biggin and Mrs. Sage. It landed 90 minutes later, near Harrow, where the two aeronauts had to be rescued by a group of boys from Harrow School from the angry farmer whose crops were damaged. *Wik (There were even suggestions that rather more amorous events had occurred in the flight.)

---

1799 The Royal Charter for the Royal Institute is promised. Ever since its founding year the Royal Institution has maintained close links with the Royal Family. On 29 June 1799, George Finch, Earl of Winchilsea (1752-1826), the President of what had until then had been called simply the “Institution” reported to a meeting of its committee of Managers ‘that he had had the Honour of mentioning this Institution to his Majesty [George III], and that his Majesty was graciously pleased to honour it with His Patronage and to allow it to be called the Royal Institution’. The actual charter was presented on January 13 in 1800. *Royal Institute web page

---

1803 An open letter to the public, and the Congress of the United States on the topic "Of The Construction of Iron Bridges" is posted by Thomas Paine. Paine had discussed this work with President Jefferson in a letter while he was in England. *The National Intelligencer and Washington Advertiser, (Washington, DC) Wednesday, June 29, 1803; Issue CCCCXIX;

---

1877 After proving that the points in a square can be put in one-to-one correspondence with the points on a line segment Cantor wrote his friend Dedekind “Je le vois, mais je ne le crois pas.” (I see it, but I don’t believe it.) [Dauben, Georg Cantor, p. 55]*VFR

---

1927 Gellivara 1073: Minor planet discovered September 14, 1923 by Johann Palisa at Vienna. Named for the small town  Gällivare in Swedish Lapland where in the year 1927 astronomers from several countries observed the Total Solar Eclipse of 1927 Named by the astronomer J. Rheden and endorsed by Anna Palisa.*NSEC
A Poster advertising viewing of Solar Eclipse from London, Midland, and Scotland Railway *GreatAmericanEclipse ‏@AmericanEclipse

---

In 1954, the Atomic Energy Commission, by a vote of 4 to 1 decided against reinstating Dr. J. Robert Oppenheimer's access to classified information. The Atomic Energy Act of 1946 required consideration of  "the character, associations, and loyalty" of the individuals engaged in the work of the Commission. Substantial defects of character and imprudent and dangerous associations, particularly with known subversives who place the interests of foreign powers above those of the United States, were considered reasons for disqualification. The Commission regarded his associations with persons known to him to be Communists exceeded tolerable limits of prudence and self-restraint, and lasted too long to be justified as merely the intermittent and accidental revival of earlier friendships.*TIS

---

1956 The interstate highway system was signed into law by President Eisenhower. Even (odd) num­bered roads run East–West (North–South) with the numbers increasing from South to North (West to East). Roads with three digit numbers are loops around cities (when the first digit is even) or spurs (first digit odd); In either case the last two digits are the main road number.  *VFR
Eisenhower had seen the speed and efficiency in moving troops and equipment on the four-lane autobahns in Germany during WW II. The idea of federal support of interstate limited-access routes in the U.S. had begun with a study under the Federal-Aid Highway Act of 1938. Little progress was made on building these roads while federal funding was low. When the Federal-Aid Highway Act of 1956 committed federal funds to the States for 90% of the cost, construction began in earnest for the System of Interstate and Defense Highways having at least four lanes with no at-grade railroad crossings. *TIS

---

2023 - My Jeannie is celebrating her birthday today, and I'm celebrating having her in my life... all the good I ever do is a reflection of a single sun.

---

BIRTHS

1716 Joseph Stepling, (29 June 1716 in Regensburg; 11 July 1778 in Prague) His fields included astronomy, physics and mathematics. At the age of 17 he documented with great accuracy the 1733 lunar eclipse. Later Euler was among his long list of correspondents. He transposed Aristotelian logic into formulas, thus becoming an early precursor of modern logic. already adopted the atomistic conception of matter he radically refused to accept Aristotelian metaphysics and natural philosophy. In 1748, at the request of the Berlin Academy, he carried out an exact observation of a solar and lunar eclipse in order to determine the precise location of Prague. During Stepling's long tenure at Prague, he set up a laboratory for experimental physics and in 1751 built an observatory, the instruments and fittings of which he brought up to the latest scientific standard.
Even though he passed up a professorship in philosophy in favor of a chair in mathematics, Empress Maria Theresa appointed him director of the faculty of philosophy at Prague as part of the reform of higher education. He was very interested in cultivating the exact sciences and founded a society for the study of science modeled on the Royal Society of London. In their monthly sessions. over which he presided until his death, the group carried out research work and investigations in the field of pure mathematics and its appiication to physics and astronomy. A great number of treatises of this academy were published.
Stepling corresponded with the outstanding contemporary mathematicians and astronomers: Christian Wolf. Leonhard Euler. Christopher Maire, Nicolas-Louis de Lacaille, Maximilian Heli, Joseph Franz, Rudjer Boskovic, Heinrich Hiss, and others. Also, Stepling was particularly successful in educating many outstanding scientists, including Johann Wendlingen, Jakob Heinisch, Johannes von Herberstein, Kaspar Sagner, Stephan Schmidt, Johann Korber, and Joseph Bergmann. After his death, Maria Theresia ordered a monument erected in the library of the University of Prague *Joseph MacDonnell, Fairfield Univ web page

---

1818 Pietro Angelo Secchi (29 June 1818 – 26 February 1878) Italian Jesuit priest and astrophysicist, who made the first survey of the spectra of over 4000 stars and suggested that stars be classified according to their spectral type. He studied the planets, especially Jupiter, which he discovered was composed of gasses. Secchi studied the dark lines which join the two hemispheres of Mars; he called them canals as if they where the works of living beings. (These studies were later continued by Schiaparelli.) Beyond astronomy, his interests ranged from archaeology to geodesy, from geophysics to meteorology. He also invented a meteorograph, an automated device for recording barometric pressure, temperature, wind direction and velocity, and rainfall. *TIS

---

1868 George Ellery Hale (June 29, 1868 – February 21, 1938) born. American astronomer known for his development of important astronomical instruments. To expand solar observations and promote astrophysical studies he founded Mt. Wilson Observatory (Dec 1904). He discovered that sunspots were regions of relatively low temperatures and high magnetic fields. Hale hired Harlow Shapley and Edwin Hubble as soon as they finished their doctorates, and he encouraged research in galactic and extragalactic astronomy as well as solar and stellar astrophysics. Hale planned and tirelessly raised funds for the 200" reflecting telescope at the Palomar Mountain Observatory completed in 1948, after his death, and named for him - the Hale telescope.*TIS

---

1893 Prasanta Chandra Mahalanobis FRS[1] (29 June 1893 – 28 June 1972) was an Indian scientist and applied statistician. He is best remembered for the Mahalanobis distance, (a statistical measure of the distance between a point P and a distribution D, - a multi-dimensional generalization of the idea of measuring how many standard deviations away P is from the mean of D. ) and for being one of the members of the first Planning commission of free india. He made pioneering studies in anthropometry in India. He founded the Indian Statistical Institute, and contributed to the design of large-scale sample surveys *Wik

---

1893 Eduard Cech, (June 29, 1893 – March 15, 1960) Czech topologist born in Stračov, Bohemia (then Austria-Hungary, now Czech Republic). His research interests included projective differential geometry and topology. In 1921–1922 he collaborated with Guido Fubini in Turin. He died in Prague. *Wik

---

1904 Topologist Witold Hurewicz (June 29, 1904 - September 6, 1956) born. Hurewicz is best remembered for two remarkable contributions to mathematics, his discovery of the higher homotopy groups in 1935-36, and his discovery of exact sequences in 1941. His work led to homological algebra. It was during Hurewicz's time as Brouwer's assistant in Amsterdam that he did the work on the higher homotopy groups; "...the idea was not new, but until Hurewicz nobody had pursued it as it should have been. Investigators did not expect much new information from groups, which were obviously commutative...". *Wik He died in 1956 when he fell off a pyramid while attending a conference in Mexico.

---

1942 K. Jon Barwise (June 29, 1942 – March 5, 2000) an American mathematician, philosopher and logician who proposed some fundamental revisions to the way that logic is understood and used.*Wik

---

DEATHS

1895 T(homas) H(enry) Huxley (4 May 1825 – 29 June 1895) was an English biologist , known as "Darwin's Bulldog" for his promotion of Darwinism which led him to an advocacy of agnosticism (a word he coined). At the age of 12 he was reading advanced works on geology, and by early adolescence he recorded the results of simple self-conducted experiments. As a ship's assistant surgeon on HMS Rattlesnake he studied marine specimens by microscope. During the 1850's he published papers on animal individuality, the cephalous mollusks (ex. squids), the methods of paleontology, and the methods and principles of science and science education. *TIS

---

1924 Robert Simpson Woodward (July 21, 1849–June 29, 1924) was an American physicist and mathematician, born at Rochester, Michigan. He graduated C.E. at the University of Michigan in 1872 and was appointed assistant engineer on the United States Lake Survey. In 1882 he became assistant astronomer for the United States Transit of Venus Commission. In 1884 he became astronomer to the United States Geological Survey, serving until 1890, when he became assistant in the United States Coast and Geodetic Survey. In 1893 he was called to Columbia as professor of mechanics and subsequently became professor of mathematical physics as well. He was dean of the faculty of pure science at Columbia from 1895 to 1905, when he became president of the Carnegie Institution of Washington, whose reputation and usefulness as a means of furthering scientific research was widely extended under his direction. He was elected to the National Academy of Sciences in 1896. In 1898-1900 he was president of the American Mathematical Society, and in 1900 president of the American Association for the Advancement of Science. In 1915 he was appointed to the Naval Consulting Board. He died in 1924 in Washington, D.C.*Wik

An illustration of the transit of Venus of 1882.
 Ceiling mural in the Paris Observatory. *Wik

---

Credits
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell

On This Day in Math - June 28

In my opinion, a mathematician, in so far as he is a mathematician, need not preoccupy himself with philosophy -- an opinion, moreover, which has been expressed by many philosophers.

Henri Lebesgue

The 179th day of the year; 

179 is a "Knockout Prime" of the form K(3,2) since 17, 19, and 79 are all prime.

179 is an emirp, a prime whose reversal, 971 is also prime, and the combination sum and product 179 * 971 + 179 + 971=174959 is also an emirp.

179³ has all odd digits, 5735339. *Derek Orr

179 is a prime whose square, 32041, has one each of the digits from 0 to 4.


179 is an emirp, a prime whose reversal, 971 is also prime, and the combination sum and product 179 * 971 + 179 + 971=174959 is also an emirp.

179 = (17 * 9) + (17 + 9)

A winning solution to the 15-hole triangular peg solitaire game is: (4,1), (6,4), (15,6), (3,10), (13,6), (11,13), (14,12), (12,5), (10,3), (7,2), (1,4), (4,6), (6,1). The term (x,y) means move the peg in hole x to y. Not only does this solution leave the final peg in the original empty hole, but the sum of the peg holes in the solution is prime. But not just any prime, it is 179.

Between the beginning and the 179th digit of π, an equal number of five different decimal digits occur (there are 18 each of the digits 0, 3, 4, 5, and 9). Mike Keith conjectures this to be the last digit of π for which this happens (there are no others up to 10^9 digits). *Prime Curios

1/179 has a repeating patter of 178 digits, called a full repetend prime.

179 is a strictly non-palindromic number. It is not a palindromic number in any base.*Wikipedia

More Math Facts for every year date here

---

EVENTS

1451 Sort of the American version of the Medes and Lydians. The Seneca and Mohawk tribes were preparing for war when a total solar eclipse swept over both their camps late in the afternoon of this early summer day. Both immediately sued for peace. (ref. DB 6/97: "A star Called the Sun" by George Gamow). *NSEC

---

1489 Last total solar eclipse on Easter Island before the one on 11 July 2012. The next will be on 25 February 2324. Ref. More Mathematical Astronomical Morsels by Jean Meeus; Willmann-Bell, 2002. *NSEC

---

1751 The first volume of Diderot’s and d’Alembert’s Encyclopedie appeared. See Hawkins, Jean d’Alembert p. 69.*VFR

---

1774 A Bill passed by Parliament included a clause to pay John Harrison for inventing a Timekeeper for finding Longitude at Sea. H5 was put on trial by the King himself in 1772, and performed superbly. The Board of Longitude, however, had refused to recognize the results of this trial, so John and William petitioned Parliament. They were finally awarded £8750 by this Act of Parliament. Perhaps more importantly, John Harrison was finally recognized as having solved the longitude problem. *Nat. Maritime Museum ‏@NMMGreenwich, *ticktocktony.com

---

1832 the first American case of a cholera epidemic was reported in New York City. Previously, Europe and the Americas were unaffected by the First Cholera pandemic of 1817 when cholera, long endemic to the Indian subcontinent, spread to Arabia, Syria, and southern Russia. This abated in the early 1820's, but a new cholera cycle began in 1826. It invaded the British Isles in Oct 1831. Canada was struck shortly before cholera reached New York. Cholera was a horrible disease, spread through fouled water. Its victims died after hours of cramps, diarrhea, and vomiting. Crowded into unsanitary slums, the poor suffered most. Many of the city's elite fled to the countryside. In America, the disease's hold broke by Dec 1832.*TIS

---

1884 Sonya Kovalevskaya officially appointed extraordinary professor at Stockholm University. [The Mathematical Intelligencer, vol. 6, no. 1, p. 29; *VFR ]

---

1949 Wolfgang Pauli writes to Carl Jung to with theories of the "Pauli effect", which Jung described as synchronicity. Pauli was famous among his colleagues for the numerous instances in which demonstrations involving equipment suffered technical problems only when he was present. He was actually banned from the laboratory of Otto Sturn a frequent dinner companion. Pauli and Jung both believed there was an effect, and tried to explain it. In this letter Pauli uses an example from the I-ching, the Chinese book of changes, to describe his thoughts on the effect. *Charles P. Enz, No Time to be Brief: A Scientific Biography of Wolfgang Pauli,

---

In 1958, the Mackinac Bridge, the world longest suspension bridge, was dedicated. Ceremonies began on 24 Jun with the first "Governor's Walk" across the bridge. (It had opened to traffic on 1 Nov 1957.) This bridge joins the upper and lower peninsulas of the state of Michigan, reducing the crossing time, from a couple of hours, to just 10 minutes. Ceremonial groundbreaking took place at the St. Ignace end of the bridge on 7 May 1954, and on the opposite shore at Mackinaw City the next day. Meanwhile caissons and superstructures were assembled as far away as Indiana, Pennsylvania and Ohio. Including approaches, the total length is 26,444-ft, needing 34 bridge support foundations. The main span is 3,800-ft long. *TIS

---

1979 New Scientist publishes "The Man Who Invented Black Holes,"  about a description of black holes from 1783 by English natural philosopher John Michell presented to the Royal Society in November, :

"Let us now suppose the particles of light to be attracted in the same manner as all other bodies with which we are acquainted; that is, by forces bearing the same proportion to their vis inertiae (or mass), of which there can be no reasonable doubt, gravitation being, as far as we know, or having any reason to believe, an universal law of nature. ... [I]f the semi-diameter of a sphere of the same density as the Sun were to exceed that of the Sun in the proportion of 500 to 1, a body falling from an infinite height towards it, would have acquired at its surface greater velocity than that of light, and consequently supposing light to be attracted by the same force in proportion to its vis inertiae, with other bodies, all light emitted from such a body would be made to return towards it by its own proper gravity."  Futility closet 

Michell's torsion balance, used in
the Cavendish experiment, *Wik

---

2009 Stephen Hawking gave a party for time travelers at 12:00 UT on this day. He did not announce the event until after it was over, and it appears that no one else cared to attend. Below is the invitation, so if you missed it up until now, it's not to late to choose not to attend. (So much for free will)

*daily Mail online

---

2011 "6.28" has become popular as Tau day with many people who think 2 pi (or 6.28...) is more appropriate, or just a nice addition to Pi-day, on March 14 (or 3.14... )

---

Births

1875 Henri Lebesgue (June 28, 1875 – July 26, 1941) He introduced the concept of Lebesgue Measure, a device for measuring the ‘length’ of complicated sets of points on the line, and so is known as the father of modern integration theory. *VFR French mathematician whose generalization of the Riemann integral revolutionized the field of integration. He was maître de conférences (lecture master) at the University of Rennes until 1906, when he went to Poitiers, first as chargé de cours (assistant lecturer) of the faculty of sciences and later as...*TIS

---

1894 Einar Hille (28 June 1894 – 12 February 1980) born. In the preface of his Analytic Function Theory (1959) he wrote “It is my hope that students of this book may come to respect the historical continuity of the subject.” More authors should include historical footnotes as good as those in this book.*VFR Hille's main work was on integral equations, differential equations, special functions, Dirichlet series and Fourier series. Later in his career his interests turned more towards functional analysis. His name persists among others in the Hille–Yosida theorem. *Wik

---

1906  Maria Goeppert Mayer (June 28, 1906 – February 20, 1972) was a German-born American theoretical physicist, and Nobel laureate in Physics for proposing the nuclear shell model of the atomic nucleus. She was the second woman to win a Nobel Prize in physics, the first being Marie Curie. In 1986, the Maria Goeppert-Mayer Award for early-career women physicists was established in her honor.

*Wik

---

1920 Nicolaas Hendrik "Nico" Kuiper (28 June 1920, Rotterdam - 12 December 1994, Utrecht) was a Dutch mathematician, known for Kuiper's test and proving Kuiper's theorem. He also contributed to the Nash embedding theorem.
Kuiper completed his Ph.D. in differential geometry from the University of Leiden in 1946 under the supervision of Willem van der Woude.
He served as director of the Institut des Hautes Études Scientifiques from 1971 to 1985.*Wik

---

1948 Kenneth Alan "Ken" Ribet (June 28, 1948 -) is an American mathematician, currently a professor of mathematics at the University of California, Berkeley. His mathematical interests include algebraic number theory and algebraic geometry.
He earned his bachelor's degree and master's degree from Brown University in 1969, and his Ph.D. from Harvard University in 1973.
Ribet is credited with paving the way towards Andrew Wiles's proof of Fermat's last theorem. Ribet proved that the epsilon conjecture formulated by Jean-Pierre Serre was indeed true, and thereby proved that Fermat's Last Theorem would follow from the Taniyama–Shimura conjecture. Crucially it also followed that the full conjecture was not needed, but a special case, that of semistable elliptic curves, sufficed. An earlier theorem of Ribet's, the Herbrand–Ribet theorem, the converse to Herbrand's theorem on the divisibility properties of Bernoulli numbers, is also related to Fermat's Last Theorem. *Wik

---

1972 Ngô Bảo Châu (June 28, 1972 - ) is a Vietnamese and French mathematician at the University of Chicago, best known for proving the fundamental lemma for automorphic forms proposed by Robert Langlands and Diana Shelstad. In 2004, Chau and Laumon were awarded the Clay Research Award for their achievement in solving the fundamental lemma proposed by Robert Langlands for the case of unitary groups. Chau also became the youngest professor in Vietnam in 2005. His proof of the general case was selected by Time as one of the Top Ten Scientific Discoveries of 2009. In 2010, he received the Fields Medal and in 2012, the Legion of Honour He is the first Vietnamese to receive the Fields Medal *Wik

---

DEATHS

1527  Abraham Ortelius, (?4 or 14 Apr 1527,  28 June 1598) a Flemish cartographer. In 1570, Ortelius published Theatrum Orbis Terrarum, or Theater of the World. This was the first modern world atlas. It contained 53 maps, and its novelty lay in the fact that the maps were uniform in style, size, and lettering; had been engraved especially for this work; had descriptive text on the back of each map; and covered the entire world, region by region. Most of the maps were not original with Ortelius—he borrowed freely from previous cartographers and he fully credited all his sources—but many of the maps, such as the world map, are brand new.

The Theatrum was an immediate publishing success, and it went through 23 editions and translations in Ortelius’ own lifetime (he died in 1598).  *Linda Hall Library

*Ortelius by Peter Paul Rubens

  

---

1768 George Hadley (12 Feb 1685; 28 Jun 1768 at age 83) English physicist and meteorologist who first formulated an accurate theory describing the trade winds and the associated meridional circulation pattern now known as the Hadley cell.*TIS Hadley died at Flitton and was buried in the chancel of Flitton church.

---

1889 Maria Mitchell (August 1, 1818 – June 28, 1889) First American professional woman astronomer, born Nantucket, Mass. While pursuing an amateur interest, on 1 Oct 1847, she gained fame from the observation of a comet which she was first to report.  She died at age 70 in Lynn, Mass.

In 1847, she discovered a comet named 1847 VI (modern designation C/1847 T1) that was later known as "Miss Mitchell's Comet" in her honor. She won a gold medal prize for her discovery, which was presented to her by King Christian VIII of Denmark in 1848. Mitchell was the first internationally known woman to work as both a professional astronomer and a professor of astronomy after accepting a position at Vassar College in 1865.[ She was also the first woman elected Fellow of the American Academy of Arts and Sciences and the American Association for the Advancement of Science

Maria Mitchell, painting by Herminia
 Borchard Dassel, 1852, *Wik

, 

---

1930 William J Greenstreet graduated from Cambridge and became headmaster of Marling School Stroud. He is best-known as the long-running editor of the Mathematical Gazette.

---

1956 Friedrich Riesz (Jan. 22, 1880, in Győr; Feb. 28, 1956, in Budapest)
One of the most significant personalities among Hungarian mathematicians.
At the beginning he studied engineering at the Technical University of Zurich, but he soon realized that he was much more interested in mathematics than in technical subjects. So he continued to study at the Royal Hungarian University of Sciences in Budapest. For him the lectures of Gyula Kőnig and József Kürschák meant the most. Then he studied for a year in Göttingen and attended the lectures of David Hilbert and Hermann Minkowski. He obtained his PhD degree and diploma of secondary school teacher of mathematics and physics in Budapest.

---

1952 William Watson (15 June 1884, Musselburgh, East Lothian, Scotland
- 28 June 1952 , Edinburgh, Scotland) graduated in Mathematics and Physics from Edinburgh University. He became head of the Physics department at Heriot Watt College in Edinburgh.*SAU

---

1972 Prasanta Chandra Mahalanobis FRS (29 June 1893 – 28 June 1972) was an Indian scientist and applied statistician. He is best remembered for the Mahalanobis distance, (a statistical measure of the distance between a point P and a distribution D, - a multi-dimensional generalization of the idea of measuring how many standard deviations away P is from the mean of D. ) and for being one of the members of the first Planning commission of free india. He made pioneering studies in anthropometry in India. He founded the Indian Statistical Institute, and contributed to the design of large-scale sample surveys *Wik

---

1893 Eduard Cech, (June 29, 1893 – March 15, 1960) Czech topologist born in Stračov, Bohemia (then Austria-Hungary, now Czech Republic). His research interests included projective differential geometry and topology. In 1921–1922 he collaborated with Guido Fubini in Turin. He died in Prague. *Wik

---

1984 Claude Chevalley (11 February 1909, Johannesburg – 28 June 1984, Paris) had a major influence on the development of several areas of mathematics including Ring Theory and Group Theory *SAU

---

1974  Vannever Bush (March 11, 1890 – June 28, 1974) American electrical engineer and administrator who and oversaw government mobilization of scientific research during World War II. At the age of 35, in 1925, he developed the differential analyzer, the world's first analog computer. It was capable of solving differential equations. He put into concrete form that which began 50 years earlier with the incomplete efforts of Babbage, and the theoretical details developed by Kelvin. This machine filled a 20 x 30 foot room. He innovated one of the largest growing media in our time, namely hypermedia as fulfilled in the Internet with hypertext links *TIS

---

1989 Charles Wilderman Trigg,(Feb 7, 1898 Baltimore, Md; June 28, 1989 San Diego, Ca.) American engineer, mathematician and educator. Educated in engineering, mathematics and education at University of Pittsburgh, University of Southern California and University of California at Los Angeles. Worked as an industrial chemist and engineer, 1917-1943, and as an educator and administrator, 1946-1963. Served in the United States Navy during World War II. Book review editor of the Journal of Recreational Mathematics. Considered one of the foremost recreational mathematicians of the twentieth century. *U of Calgary Archives

---

2015 Louis Norberg Howard, (12 March, 1929; Chicago, Il - June 28,2015) emeritus professor of mathematics at MIT, and McKenzie emeritus professor at Florida State University, died on Sunday, at the age of 86.
Howard joined the MIT mathematics faculty in 1955 as an assistant professor, and was promoted to full professor in 1964. He retired from MIT in 1984.
Howard was an applied mathematician who worked primarily in the field of fluid dynamics. He made fundamental contributions to a broad range of subjects, including hydrodynamic stability and geophysical flows. He made a number of key advances in our understanding of turbulent convection, flows in Hele-Shaw cells, salt-finger zones, rotating flows, and reaction-diffusion equations. The power of his mathematical modeling was evident when he transformed qualitative ideas about the bounds on turbulent transport into rigorous mathematical arguments that initiated the field of upper-bound theory.
He received his BA in physics from Swarthmore College in 1950, and his MA and PhD in mathematical physics from Princeton, in 1952 and 1953, respectively, under the supervision of Donald Spencer. He took an appointment as a Higgins lecturer in mathematics at Princeton in 1953, after which he became a research associate in mathematics and aeronautics at Caltech in 1955.
Howard was named a fellow of the American Academy of Arts and Sciences in 1965 and the American Physical Society in 1984, and was elected to the National Academy of Sciences in 1977. In 1997, he was honored with the prestigious Fluid Dynamics Prize of the American Physical Society. *MIT News

---

Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell

On This Day in Math - June 27

 

Every science that has thriven has thriven upon its own symbols: logic, the only science which is admitted to have made no improvements in century after century, is the only one which has grown no symbols.
Augustus de Morgan


The 178th day of the year; 178 = 2 x 89. Note that 2 and 89 are the smallest and the largest Mersenne prime exponents under 100. *Prime Curios

178 is a palindrome in base 6,\( [454]_6 \) and in base 8 \([262]_8\)

Strangely enough, 178 and 196 are related... In fact, 178 has a square with the same digits as 196:
178² = 31,684
196² = 38,416
178 also has a cube with the same digits as 196:
178³ = 5,639,752
196³ = 7,529,536
*Zoo of Numbers

178 = 13^2 + 3^2

178 is a palindrome in base 6 (454), base 7 (343), and base 8 (262)

178 is a semi-prime, the product of 2 and 89, which are the smallest, and largest Mersenne prime exponents under 100.

More Math Facts for each year day here.

---

EVENTS

432 B.C. Meton observed the summer solstice and began his cycle. Meton was one of the first Greek astronomers to make accurate astronomical observations. It is widely believed that, working with Euctemon, he observed the summer solstice, which marked the Athenian New Year, in 432 BC.
The Metonic cycle appears in the oldest known astronomical device, the Antikythera Mechanism (2nd century BC) together with its multiple the Callippus cycle of 76 years.
The foundations of Meton's observatory in Athens are still visible just behind the podium of the Pnyx, the ancient parliament. Meton found the dates of equinoxes and solstices by observing sunrise from his observatory. The bisectrice of the observatory lies in an easterly direction, between the Acropolis and the Lycabetus hill.*Wik

---

1739 "Heavens!, Maupertuis is a flea. Is he ever in one place?" So wrote Francoise de Graffigny to a friend about the French mathematician/man of letters, Pierre-Louis Moreau de Maupertuis. Graffigny affectionately gave the nickname to describe his "frenetic ubiquity." *Mary Terrall, The Man Who Flattened the Earth.

---

In 1847, New York and Boston were linked by telegraph wires. This enabled the New York newspapers to receive foreign news brought by Cunard's steamers to the Boston port about 190 miles away. When the Cambria next arrived in Boston, three New York Newspapers on 18 Jul 1846 carried identical brief first-day telegraphic summaries of the Cambia's news*. This telegraph link opened three years after the first U.S. telegraph line was opened on 24 May 1844 with a message sent by Samuel Morse 80 miles from Washington D.C. and Baltimore, Md.*TIS

---

1908 The academy of sciences of Gottingen announced a prize of one hundred thousand marks, according to the will of Dr. Paul Wolfskehl, of Darmstadt, for the proof of Fermat’s great theorem. A German industrialist and amateur mathematician, Wolfskehl bequeathed 100,000 marks to the Göttingen Academy of Sciences to be offered as a prize for a complete proof of Fermat's Last Theorem. On 27 June 1908, the Academy published nine rules for awarding the prize. Among other things, these rules required that the proof be published in a peer-reviewed journal; the prize would not be awarded for two years after the publication; and that no prize would be given after 13 September 2007, roughly a century after the competition was begun. Wiles collected the Wolfskehl prize money, then worth $50,000, on 27 June 1997.
Prior to Wiles' proof, thousands of incorrect proofs were submitted to the Wolfskehl committee, amounting to roughly 10 feet (3 meters) of correspondence. In the first year alone (1907–1908), 621 attempted proofs were submitted, although by the 1970s, the rate of submission had decreased to roughly 3–4 attempted proofs per month. According to F. Schlichting, a Wolfskehl reviewer, most of the proofs were based on elementary methods taught in schools, and often submitted by "people with a technical education but a failed career". In the words of mathematical historian Howard Eves, "Fermat's Last Theorem has the peculiar distinction of being the mathematical problem for which the greatest number of incorrect proofs have been published."*Wik

---

1966 An almost 300 year old conjecture of Leonhard Euler is proven wrong. Euler had conjectured that, in the fashion that \(x^2 + y^2 = z^2 \) it always takes n terms to sum to an n-th power: two squares, three cubes, four fourth powers,etc. In 1966, L. J. Lander and T. R. Parkin found the first counterexample: four fifth powers that sum to a fifth power. They showed that \( 27^5 + 84^5 + 110^5 + 133^5 = 144^5.\) In 1988 Noam Elkies of Harvard University found a counterexample for fourth powers: \(2,682,440^4 + 15,365,639^4 + 187,960^4 = 20,615,673^4. Subsequently, Roger Frye of Thinking Machines Corporation did a computer search to find the smallest example: 95,800^4 + 217,519^4 + 414,560^4 = 422,481^4.*David Darling

---

1967 The first ATM in England that was put into use was by Barclays Bank in Enfield Town in North London, United Kingdom, on 27 June 1967. This machine was the first in the UK and was used by English comedy actor Reg Varney, at the time so as to ensure maximum publicity for the machines that were to become mainstream in the UK. This instance of the invention has been credited to John Shepherd-Barron of printing firm De La Rue, who was awarded an OBE in the 2005 New Year's Honours List. His design used special cheques that were matched with a personal identification number, as plastic bank cards had not yet been invented. *Wik (The plaque posted at the sight makes the claim to be the first cash machine in the world, but cash dispensing machines had been installed in Tokyo and another shortly after in Upsalla.)

---

1977 In 1983, Sally Ride became the first American woman in space. She blasted off aboard Challenger, culminating a long journey that started in 1977 when the Ph.D. candidate answered an ad seeking astronauts for NASA missions.

In a lecture she gave at Berkeley, Ride said she saw the ad on Page 3 of the student newspaper.  "The moment I saw that ad, I knew that's what I wanted to do," she said.

By the time Ride decided to apply to become an astronaut, she had already received degrees in physics and English and was on her way to a Ph.D. in physics from Stanford University.

*HT Lunar Heritage

---

1977 Italy issued a postage stamp honoring Filippo Brunelleschi (1377–1446). [Scott #1266]. *VFR

---

1980 Creighton Carvello recited 20,013 digits of π from memory in nine hours and one minute. *VFR

---

BIRTHS

1767 Alexis Bouvard (27 June 1767 – 7 June 1843) French astronomer and director of the Paris Observatory, who is noted for discovering eight comets and writing Tables astronomiques of Jupiter and Saturn (1808) and of Uranus (1821). Bouvard's tables accurately predicted orbital locations of Jupiter and Saturn, but his tables for Uranus failed, leading him to hypothesize that irregularities were caused by an unknown perturbing body. This spurred observations leading to the discovery of Neptune by Adams and Leverrier.*TIS

---

1806 Augustus de Morgan (27 June 1806 – 18 March 1871) born in Madura (now Madurai), India, son of a colonel in the Indian Army. He is best known for his work in Formal Logic. “De Morgan’s Laws”, are contained in his first book (1847), although they were known to Peter of Spain in the fourteenth century. *VFR

The rules can be expressed in English as:

"The negation of a conjunction is the disjunction of the negations." and
"The negation of a disjunction is the conjunction of the negations."

*Wik
When he defined and introduced the term "mathematical induction" (1838), he gave the process a rigorous basis and clarity that it had previously lacked. He originated the use of the slash to represent fractions, as in 1/5 or 3/7. In Trigonometry and Double Algebra (1849) he gave a geometric interpretation of complex numbers. *TIS  A nice blog about De Morgan's life and relationships is at The Renaissance Mathematicus.

---

1850 Jorgen Pedersen Gram.(June 27, 1850 – April 29, 1916) Danish mathematician. Today he is best known for his criterion of linear independence of functions. The Gram-Schmidt Orthonormal Basis Theorem in Linear Algebra was first published by him in 1883.
1940 Daniel G. Quillen bon in Orange, New Jersey. In 1978 he won a Fields Medal as the “prime architect of the higher algebraic K-theory, a new tool that successfully employed geometric and topological methods and ideas to formulate and solve major problems in algebra, particu¬larly ring theory and module theory.” *VFR French mathematician who is known for her work in number theory and contributions to the applied mathematics of acoustics and elasticity. Germain was self-taught from books, and from lecture notes supplied by male friends attending the Ecole Polytechnique which she, as a woman, was not permitted to attend. Using a male pseudonym, M. LeBlanc, she corresponded with Lagrange who recognised her skill, and subsequently sponsored her work. She accomplished a limited proof of Fermat's last theorem, for any prime under 100 where certain conditions were met. In 1816, she won a prize sponsored by Napoleon for a mathematical explanation of Chladni figures, the vibration of elastic plates. She died at age 55, from breast cancer. TIS

---

1931 Martinus Justinus Godefriedus Veltman (born June 27, 1931 in Waalwijk) is a Dutch theoretical physicist. He shared the 1999 Nobel Prize in physics with his former student Gerardus 't Hooft for their work on particle theory. In 1963/64, during an extended stay at SLAC he designed the computer program Schoonschip for symbolic manipulation of mathematical equations, which is now considered the very first Computer algebra system. He was awarded the Nobel Prize for Physics in 1999 together with 't Hooft, "for elucidating the quantum structure of electroweak interactions in physics". Veltman is now retired and holds a position of Emeritus Professor at the University of Michigan. Asteroid 9492 Veltman is named in his honor. *Wik

---

DEATHS

1829 James Smithson (ca. 1765 – 27 June 1829) English scientist who provided funds in his will for the founding of the Smithsonian Institution, Washington, D.C. "for the increase and diffusion of knowledge." He had inherited his fortune chiefly through his mother's family. He was a chemist and minerologist who published 27 scientific papers. The mineral smithsonite (carbonate of zinc) was named for him.*TIS

---

1831 Sophie Germain (April 1, 1776 – June 27, 1831)died before she could receive the honorary doctorate Gauss had persuaded the University of Gottingen to give her. *VFR

---

1880 Carl Borchardt (22 February 1817 – 27 June 1880) was a German mathematician who worked in a variety of areas in analysis. He edited Crelle's Journal for more than 30 years.*SAU

---

1952 Max Dehn died (November 13, 1878 – June 27, 1952). He solved Hilbert’s third problem in 1900 (shortly after receiving his Ph.D. un¬der Hilbert on another topic in the foundations of geometry): a tetrahedron cannot be cut up into finitely many pieces and reassembled into a cube of equal volume. Thus Dehn became the first mathematician to join “the honors class” of mathematicians who had solved one of the twenty-three problems Hilbert posed in Paris in 1900.

---

1975 Sir Geoffrey Ingram Taylor OM (7 March 1886 – 27 June 1975) was a British physicist, mathematician and expert on fluid dynamics and wave theory. His biographer and one-time student, George Batchelor, described him as "one of the most notable scientists of this (the 20th) century". His final research paper was published in 1969, when he was 83. In it he resumed his interest in electrical activity in thunderstorms, as jets of conducting liquid motivated by electrical fields. The cone from which such jets are observed is called the Taylor cone for his namesake. In the same year Taylor was appointed to the Order of Merit. He suffered a stroke in 1972 which effectively put an end to his work; he died in Cambridge in 1975.*Wik

---

---

1924 Evelyn Boyd Granville (May 1, 1924 - June 27, 2023 ) was the second African-American woman in the U.S. to receive a PhD in mathematics. (The first was Euphemia Haynes who was awarded her PhD from Catholic University in 1943.)

With financial support from her aunt and a small partial scholarship from Phi Delta Kappa, Granville entered Smith College in the fall of 1941. She majored in mathematics and physics, but also took a keen interest in astronomy. She was elected to Phi Beta Kappa and to Sigma Xi and graduated summa cum laude in 1945. Angeles]]. In L.A., Granville accepted the position of Research Specialist with the Space and Information Systems Division of the North American Aviation Company, but returned to IBM the following year. Both positions involved trajectory analysis and orbit computation. In 1967, Granville’s marriage ended in divorce. At the same time, IBM was cutting staff in Los Angeles, so Granville applied for a teaching position at California State University in Los Angeles, California.
She moved to California State University at Los Angeles in 1967 as a full professor of mathematics and married Edward V. Granville in 1970. After retiring from California State in 1984 she joined the faculty of the University of Texas at Tyler as professor and chair of mathematics. There she developed elementary school math enrichment programs. One of three African American women honored by the National Academy of Science in 1999, she has been awarded honorary degrees by Smith College and Lincoln University. 

Granville died at her apartment in Silver Spring, Maryland on June 27, 2023, at the age of 99*Wik

Dr. Scott Williams at Buffalo has a website about Black Women in Mathematics including many biographies.

Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell