Friday, 21 September 2012
Houses and Utilities / Why it Can't be Done
By the time they reach high school, most students have encountered the problem of connecting the three houses to three utilities stated below:
Given three houses, A, B, and C; and three utilities, E, G, and W draw a connection from each utility to each house without the lines crossing. (The pretty image above came from the Math Forum web site, but I had already written my solution using A, B, and C so ... )
Although the problem usually comes with a location of the houses and utilities, such as the picture at right, they may actually be placed anywhere on a plane, or a sphere, and the problem is still the same.
A brief history of the game is taken from a note from David Singmaster,
Gas, Water and Electricity. Dudeney's Amusements in Mathematics (AM)(1917) describes this as being 'as old as the hills', but {this was the} earliest known reference until I found Dudeney's column in Strand Magazine 46 (Jul 1913) 110, but this still
says: "It is much older than electric lighting, or even gas ...."
In Sam Loyd and His Puzzles (1928), Sam Loyd Jr says he brought out the puzzle about 1900. Dudeney's Strand column says he has recently had four letters from the US about it. {Loyd was a US puzzle writer, Dudeney was in the UK)
Most students have tried this so often that they feel certain it is really not possible. Below I will try to provide two very different explanations as to why it is impossible to draw the figure on a plane or sphere.
A proof using the Jordan Curve Theorem
If we ignore, for a moment, the water plant and house C, however we place the utilities and houses A and B it should seem clear that G must connect to A and B, and E must connect to A and B also, and so a circuit GAEB must be formed from G to A to E to B. The Jordan Curve theorem says (in more formal language) that a closed curve, such as the circuit GAEB divides the plane (and the sphere) into two regions, we can call them the inside and the outside for our informal explanation.
Now what happens when we wish to place w, the water plant, on our picture. It could be inside, or outside. We will assume first that it lies inside the curve GAEB. and when it is connected to A and B, as shown at right, it will divide the inside into two smaller regions, which we will call inside1 (inside GBWA) and inside2(inside BWAE).
Now all we have to do is find a place for house C and we are done. House C could be placed in the outside region, but from there it could not be connected to W without crossing. House C could be placed in inside1, but from there it could not be connected to E without a crossing. Or we could place house C in inside2, but from there it cannot be connected to G without a crossing. We have shown that if W is placed inside, there is no way to place C without a crossing. The other place to put W is in the outside, but a similar proof will show that C cannot be connected then either. Can you complete the proof?
If we visualize the graph above as being on a sphere (think of the Earth), there is no loss of generality if we assume that points G, B, E, and A all lie on the equator. If W is placed in the Northern Hemisphere, or in the Southern, the picture, and the proof, is exactly the same.
A Proof Using Euler’s Theorem for Planer Graphs
Euler’s famous theorem says that in any planer graph (one that can be drawn without crossings) the relationship between vertices, V, edges, E, and faces, F, obeys the relationship V + F = E + 2. Let’s assume that in spite of all our efforts there really is a way to connect the vertices with non-crossing edges. Then there would be a planer graph with nine edges (E=9) and six vertices (V=6) . Using these two values in Euler’s equation we come to the conclusion that the number of faces, F, must be the solution to 6 + F = 9 + 2. That means there will be five faces to the plane figure.
So what is wrong with that? To answer that question we need to take a small diversion and look at some relationships in planer graphs in general. We will illustrate our point with the simple planer graph at the right, which has four faces and seven edges.
One way to count the edges would be to count the number of edges on each face. For example, Face 1 has 3 edges, face 2 has 4 edges, face 3 has 3 edges, and face 4 which goes all around the other three, has four edges. Notice that when we add all these up we get 4+3+4+3 = 14, but there are only 7 edges. Since each edge joins two faces, when we count the edges on the faces, we will get twice the number of edges as actually exist. Written algebraically this would be which just says that if you add up the number of edges on each face, you get twice the number of edges that really exist. So 2E/F would give us the average number of edges on the faces of a planer Graph. Now we are ready to use this idea of the average number of edges on a face to conclude our original proof. Remember that we found that if a planer graph was possible for the electricity problem, that there would have to be 5 faces on it, but we also knew it had 9 edges. So the average number of edges on each face, 2E/F will be 2(9)/5 = 3.6. But remember what the faces looked like in our problem; each face was created by at least four edges, utility to house to utility to house and back to utility. No face in this graph can have less than four edges, so an average of 3.6 is impossible, and we are forced to admit that no such planer graph can exist.
But on Some Shapes, It is Possible.
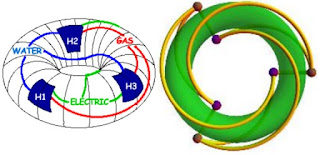
A torus is the mathematical name for a shape like a doughnut or inner tube from automobile tire. Can you convince yourself that the connections can be made without crossing on such a solid? Here is an illustration from Alexander Bogomolny's wonderful "Cut the Knot" Web site.
Can it be done on a Mobius’ Strip?
I should add here that this graph, called K3,3 in graph theory is part of a famous 1929 proof by Kuratowski which bears his name that shows that ANY graph that is NOT planer has a subgraph which is either K3,3 or K5 (think of a pentagon with a pentagram drawn inside it).
Subscribe to:
Post Comments (Atom)



No comments:
Post a Comment