Scientists have one thing in common with children: curiosity. To be a good scientist you must have kept this trait of childhood, and perhaps it is not easy to retain just one trait. A scientist has to be curious like a child; perhaps one can understand that there are other childish features he hasn't grown out of.
~Otto Robert Frisch
The 274th day of the year; 274 is a tribonacci number..The tribonacci numbers are like the Fibonacci numbers, but instead of starting with two predetermined terms, the sequence starts with three predetermined terms and each term afterwards is the sum of the preceding three terms. The first few tribonacci numbers are 0, 0, 1, 1, 2, 4, 7,
1386 University of Heidelberg founded. The Ruprecht-Karls-Universität Heidelberg (Heidelberg University, Ruperto Carola) is a public research university located in Heidelberg, Baden-Württemberg, Germany. It is the oldest university in Germany and was the fourth university established in the Holy Roman Empire. A coeducational institution since 1899, today Heidelberg consists of twelve faculties and offers degree programs at undergraduate, graduate and postdoctoral levels in some 100 disciplines. *Wik
1610 Lodovico Cigoli writes to Galileo to inform him that Father Christoph Clavius SJ, the senior mathematician at the Collegio Romano, had said that if the telescope revealed four
new ‘planets’ around Jupiter to Galileo, then Galileo must have put them in the telescope to begin with. Two months later, Clavius had observed Jupiter’s moons himself. *Albert Van Helden, Galileo and the telescope, The origins of the telescope, Royal Netherlands Academy of Arts and Sciences, Amsterdam 2010
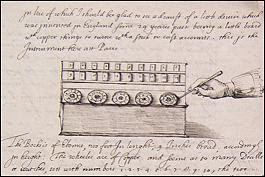
1648 In a letter to Samuel Hartlib, Sir Balthazar Gerbier sends a description of Pascal's mechanical calculator. Wikipedia describes Gerbier as "an Anglo-Dutch courtier, diplomat, art advisor, miniaturist and architectural designer." Nathan Kesling @nathan13109
1658 The closing date for Pascal’s prize problems on the cycloid. (T. Christie advised me that some give the date as Oct 2). A toothache earlier that year caused him to return to mathematics and to study the cycloid. In 1654, late in the evening Pascal experienced a religious ecstasy that called him to give up his intermittent interest in mathematics and to devote his time to religious contemplation. For years he devoted no time to mathematics. Then one night, unable to sleep because of an abscessed tooth, Pascal began to think about some problems about the cycloid. His pain disappeared and he interpreted this as a sign that God was pleased by his mathematical studies. In a brief time he completed the investigationof the cycloid. Then he established a contest about the cycloid with himself and Roberval as the judges. The three problems he asked were:
1. Find the area and the center of gravity of the region BCD bounded by the cycloid, the horizontal line BC and the axis of symmetry AD.
2. Find the volume and center of gravity of the solids obtained by revolving the region BCD about AD and about BC.
3. For the solids in the previous question, find the center of gravity of the solids formed when each is cut by a plane parallel to its axis of revolution.
Only two contestants submitted solutions. No prize was awarded as the judges declared that the solutions were either incomplete or incorrect. Pascal then published his own results in a paper entitled "L'Histoire de la Roulette". It is worth noting that all these investigations of the cycloid occurred before Newton and Leibnitz' work on the calculus! *Historical Modules for the Mathematical Classroom There is a famous statue by Pajou in the Louvre of Pascal in which he is contemplating the Roulette (cycloid). (And in this photo, I am contemplating him contemplating the roulette) More on the cycloid, including a close up of the tablet in the statue is here.
1670 James Gregory writes to John Collins, with the first use of what will come to be called the Newton-Gregory interpolation formula. He includes in the letter two enclosures showing how to apply his method to series for sines and logarithms. *Beery & Stedall, Thomas Harriot’s Doctrine of Triangular Numbers, pg 51-52
1752 A letter of Benjamin Franklin written on October 1st, to Mr. Peter Collinson, FRS concerning an electrical kite, was read before the society on Dec 21. Franklin describes the construction of the kite from two light strips of cedar and a large thin silk handkerchief,
1831 Michael Faraday discovers induced electric current using a helix made of two coils each of 203 feet of insulated copper wire. "A sudden jerk was perceived when the battery communication was made and broken... it was one way when made, and the other when broken." *A history of physics in its elementary branches By Florian Cajori
1842 Arthur Cayley's acceptance to Trinity was announced on this day. He was twenty-one years old and accepted on his first sitting, a rare event. He was the youngest man admitted to Trinity in the 19th Century. * A. J. Crilly, Arthur Cayley: Mathematician Laureate of the Victorian Age
1847 Maria Mitchell sees a comet... the first woman astronomer in the United States discovered a comet. On this night in the Autumn of 1847, Maria looked at the sky through the telescope in her homemade observatory at Nantucket, Mass. and saw a star five degrees above the North Star where there had been no star before. She had memorized the sky and was sure of her observation. It occurred to her that this might be a comet. Maria recorded the presumed comet's coordinates. The next night the star moved again. This time she was sure it was a comet. For this discovery, she was awarded a gold medal by the king of Denmark. She became the first woman elected to the American Academy of Arts and Sciences. *TIS
1861 On Oct 1, a seemingly depressed Charles Darwin writes, "My Dear Lyell, ... I am very poorly today & very stupid & hate everybody & everything. One lives only to make blunders.–... I am
Ever yours
C. Darwin
1891 On Oct 1 Stanford University opened its doors after six years of planning and building. The prediction of a New York newspaper that Stanford professors would "lecture in marble halls to empty benches" was quickly disproved. The first student body consisted of 555 men and women, and the original faculty of 15 was expanded to 49 for the second year. The university’s first president was David Starr Jordan, a graduate of Cornell, who left his post as president of Indiana University to join the adventure out West.
The Stanfords engaged Frederick Law Olmsted, the famed landscape architect who created New York’s Central Park, to design the physical plan for the university. The collaboration was contentious, but finally resulted in an organization of quadrangles on an east-west axis. Today, as Stanford continues to expand, the university’s architects attempt to respect those original university plans. *Stanford Univ Web page
1895 On the first of October 1895, the first German institute of insurance science was founded at the University of Göttingen, as a result of joint efforts of Felix Klein (1849-1825) and his fellow student Ludwig Kiepert (1846-1934), who was then chairman of the Prussian Civil Service Association (today called Hannover Life Insurance).This was the first institute in Germany in which a curriculum in actuarial mathematics, insurance law, and insurance economics was offered. Successful studies led to the degree “Versicherungsverständiger” (insurance expert). The institute was divided into a mathematical section and an administrative section, and its first chairman was Wilhelm Lexis. *From Center for Statistics, History of Statistics in Gottingen.
1907 Delegates from 310 Esperanto societies throughout the world met to elect a committee to modify the language. Louis Couturat, influenced by Leibniz’s thought on the construction of a logical universal language, was elected one of the secretaries. *VFR
1934 Paul Erdos stops in Cambridge to visit with mathematical friends, particularly Harrold Davenport and Richard Rado, on his way to a position in Manchester. *Bruce Schechter, My Brain is Open: The Mathematical Journeys of Paul Erdos
1954 IBM announced is 705 EDP, part of its 700 series of mainframe computers. A business-oriented machine, the 705 had magnetic core memory.*CHM
1969 Concorde goes Mach 1 In 1969, the prototype French-built Concorde broke the sound barrier for the first time. The inaugural flight of the aircraft had taken place on 2 Mar 1969 in Toulouse, France, and its first commercial flight was on 21 Jan 1976. It was the first plane in the world to be entirely controlled by computer. As the only supersonic passenger aircraft, the Anglo-French Concorde remains a brilliant technological achievement, though its impact on international air travel has been limited by the high cost of buying and operating the aircraft. There was also widespread opposition from environmental groups on the grounds of the Concorde's noise on takeoff and its fuel consumption. Only British Airways and Air France have operated the aircraft. *TIS
1988 The game Connect Four Solved first by James D. Allen (Oct 1, 1988), and independently by Victor Allis (Oct 16, 1988). First player can force a win. Strongly solved by John Tromp's 8-ply database (Feb 4, 1995). Weakly solved for all boardsizes where width+height is at most 15 (Feb 18, 2006). *Wik
2012 With God's grace, Dame Kathleen Ollerenshaw will awake for her 100th birthday today. Happy Birthday to a Grand-Ol-Dame, and may a puzzle occupy her thoughts. (See 1912 Births below).
(she did indeed greet her 100 th birthday, but Died: August 10, 2014, Didsbury, Manchester, United Kingdom)
1535 Giambattista della Porta (? Oct 1535 - 4 Feb 1615) Italian natural philosopher, experimenter and mathematician, though he also sought the miraculous or magical. He studied optics, including refraction (De refractione, 1593). Porta did not invent the telescope, regardless of his published claim. He was the first to propose adding a convex lens to the camera obscura, and first to recognize the heating effect of light rays. He wrote on cryptography in De furtivis literarum (1563), and his other books included mechanics, squaring the circle, description of a steam engine in De spiritali (1606). He formed the society, Accademia dei Segreti, dedicated to discussing and studying nature, meeting at his home, until closed by the Inquisition (about 1578). *TIS
1671 Luigi Guido Grandi was an Italian Jesuit who worked on geometry and hydraulics.Grandi was the author of a number of works on geometry in which he considered the analogies of the circle and equilateral hyperbola. He also considered curves of double curvature on the sphere and the quadrature of parts of a spherical surface.
In 1701 Grandi discussed the conical loxodrome, the curve that cuts the generators of a cone of revolution in a constant angle. He studied the curve the Witch of Agnesi in 1703. In fact his work of 1703 is important in introducing Leibniz's calculus into Italy.
In 1728 Grandi published Flores geometrici a work in which he defines the clelie curve. He named the curve after Countess Clelia Borromeo and dedicated his book to her. If the longitude and colatitude of a point P on a sphere is denoted by θ and φ and if P moves so that θ = m φ, where m is a constant, then the locus of P is a clelie. Grandi also applied the term "clelies" to the curves determined by certain trigonometric equations involving the sine function
a sin θ = b sin mφ
a sin θ = a - b sin mφ
Grandi also worked on hydraulics and was involved with a number of projects such as ones to drain the Chiana Valley and the Pontine Marshes. He also published a number of works on mechanics and astronomy. His practical work on mechanics included experimenting with a steam engine. *SAU
He is noted for the roses that he introduced. His idea was to find a geometrical definition of curves which resemble flowers. These curves are still part of our calculus courses, except now we use polar coordinates to define them.*VFR
1873 Alfreds Arnolds Adolfs Meders (1 Oct 1873 , 1944) Meders worked on differential geometry and mathematical analysis. He often published papers written in German, in German journals. For example he published the following three papers in Crelle's Journal: Über einige Arten Singularer Punkte von Raumkurven (1896); Zur Theorie der singularen Punkte einer Raumkurve (1899); and Analytische Untersuchung singularer Punkte von Raumkurven (1910). In Monatshefte für Mathematik he published: Über die Determinante von Wronski (1906); and Zur Differentiation bestimmter Integrale nach einem Parameter (1911).Meders was also interested in the history of mathematics and he wrote an important paper Direkte und indirekte Beziehungen zwischen Gauss und der Dorpater Universität (Direct and indirect connections between Gauss and the University of Dorpat) in 1928. His interests went outside mathematics and he sometimes lectured on astronomy, meteorology and biology where he had a special interest in birds. *SAU
1898 Béla Kerékjártó (October 1, 1898, –June 26, 1946) was a Hungarian mathematician who wrote numerous articles on Topology. He earned his Ph.D. degree from the University of Budapest. He taught at the Faculty of Sciences of the University of Szeged from 1922, and at the University of Budapest from 1938. In 1923, he published one of the first books on Topology; Hermann Weyl wrote that this book completely changed his views of the subject.*Wik
1904 Otto Robert Frisch (1 Oct 1904; 22 Sep 1979) Austrian-British nuclear physicist, born in Vienna, who, with his aunt Lise Meitner, described the division of neutron-bombarded uranium into lighter elements. He named the process fission, borrowing a term from biology (1939). At the time, Meitner was working in Stockholm and Frisch (1934-39) at Copenhagen under Niels Bohr, who brought their observation to the attention of Albert Einstein and others in the United States. He did research with James Chadwick 1940-43, and was head of the Critical Assembly Group on the Los Alamos project 1943-46. After World War II, Frisch became a science writer on atomic physics for the layman. *TIS
1911 Zhou Weiliang (simplified Chinese: (October 1, 1911– August 10, 1995) was a Chinese mathematician born in Shanghai, known for his work in algebraic geometry.
He was a student in the USA, graduating from the University of Chicago in 1931. In 1932 he attended the University of Göttingen, then transferring to Leipzig where he worked with van der Waerden. They produced a series of joint papers on intersection theory, introducing in particular the use of what are now generally called Chow coordinates (which were in some form familiar to Arthur Cayley).
He married Margot Victor in 1936, and took a position at the National Central University in Nanjing. His mathematical work was seriously affected by the wartime situation in China. He taught at the National Tung-Chi University in Shanghai in the academic year 1946–47, and then went to the Institute for Advanced Study in Princeton, where he returned to his research. From 1948 to 1977 he was a professor at Johns Hopkins University. *Wik
1912 Dame Kathleen Mary Ollerenshaw, née Timpson, DBE (1 October 1912, August 10, 2014, Didsbury, Manchester, United Kingdom ) is a British mathematician and politician. Deaf since the age of eight, she loved doing arithmetic problems as a child. As a young woman, she attended St Leonards School and Sixth Form College in St Andrews, Scotland where today the house of young male boarders is named after her. At the age of 19, she gained admittance to Somerville College, Oxford to study mathematics. She completed her doctorate at Somerville in 1945 on "Critical Lattices" under the supervision of Theo Chaundy. She wrote five original research papers which were sufficient for her to earn her DPhil degree without the need of a formal written thesis.
Ollerenshaw served as a Conservative Councillor for Rusholme for twenty-six years (1956–1981), was Lord Mayor of Manchester (1975–1976), and the prime motivator in the creation of the Royal Northern College of Music. She was made a Freeman of the City of Manchester and was an advisor on educational matters to Margaret Thatcher's government in the 1980s.
She has published at least 26 mathematical papers, her best-known contribution being to most-perfect pandiagonal magic squares. An annual public lecture at the School of Mathematics, University of Manchester is named in her honour.
An amateur astronomer, Ollerenshaw donated her telescope to Lancaster University, and an observatory there bears her name. She is an honorary member of the Manchester Astronomical Society and held the post of Vice President for a number of years. *Wik A wonderful article about her approaching her 100th birthday is in Scientific American.
 1768 Robert Simson (14 October 1687 – 1 October 1768) was a Scottish mathematician and professor of mathematics at the University of Glasgow. The pedal line of a triangle is sometimes called the "Simson line" after him. Edmond Halley suggested to him that he might devote his considerable talents to the restoration of the work of the early Greek geometers, such as Euclid and Apollonius of Perga. These are works that only survive in abbreviated accounts given by later mathematicians such as Pappus of Alexandria. He first studied Euclid's so-called porisms. Playfair's 1792 definition of porism is "a proposition affirming the possibility of finding such conditions as will render a certain problem indeterminate, or capable of innumerable solutions."
1768 Robert Simson (14 October 1687 – 1 October 1768) was a Scottish mathematician and professor of mathematics at the University of Glasgow. The pedal line of a triangle is sometimes called the "Simson line" after him. Edmond Halley suggested to him that he might devote his considerable talents to the restoration of the work of the early Greek geometers, such as Euclid and Apollonius of Perga. These are works that only survive in abbreviated accounts given by later mathematicians such as Pappus of Alexandria. He first studied Euclid's so-called porisms. Playfair's 1792 definition of porism is "a proposition affirming the possibility of finding such conditions as will render a certain problem indeterminate, or capable of innumerable solutions."Simson's work on Euclid's porisms was published in 1723 in the Philosophical Transactions of the Royal Society, and his restoration of the Loci Plani of Apollonius appeared in 1749. Further work of his on porisms and other subjects including logarithms was published posthumously in 1776 by Lord Stanhope at his own expense. Simson also set himself the task of preparing an edition of Euclid's Elements in as perfect a form as possible, and his edition of Euclid's books 1-6, 11 and 12 was for many years the standard text and formed the basis of textbooks on geometry written by other authors. The work ran through more than 70 different editions, revisions or translations published first in Glasgow in 1756, with others appearing in Glasgow, Edinburgh, Dublin, London, Cambridge, Paris and a number of other European and American cities. Recent editions appeared in London and Toronto in 1933 under the editorship of Isaac Todhunter, and in São Paolo in 1944. Simson's lectures were delivered in Latin, at any rate at the beginning of his career. His most important writings were written in that language, however, his edition of Euclid, after its first publication in Latin, appeared in English, as did a treatise on conic sections that he wrote for the benefit of his students.
the Simson line does not appear in his work but Poncelet in Propriétés Projectives says that the theorem was attributed to Simson by Servois in the Gergonne's Journal. It appears that the theorem is due to William Wallace.
The University of St Andrews awarded Simson an honorary Doctorate of Medicine in 1746.
In 1753 Simson noted that, as the Fibonacci numbers increased in magnitude, the ratio between adjacent numbers approached the golden ratio, whose value is
1924 John Edward Campbell is remembered for the Campbell-Baker-Hausdorff theorem which gives a formula for multiplication of exponentials in Lie algebras. *SAU(1 + √5)/2 = 1.6180 . . . . *SAU
1972 Francisco José Duarte (6 Jan 1883, 1 Oct 1972) Duarte's most important work in mathematics was done in algebra, number theory and mathematical analysis. His first work in mathematics was about which he presented to the Paris Academy of Sciences in 1907. He published papers on the general solution of a diophantine equation of the third degree x3 + y3 + z3 - 3xyz = v3, simplified Kummer's criterion and gave a simple proof of the impossibility of solving the Fermat equation x3 + y3 + z3 = 0 in nonzero integers. He also observed that the interpolation formula of Everett is a consequence of the interpolation formula of Gauss. In 1908 he published an article where he calculated π to 200 decimal places.
His main three books are: Monograph on the numbers π and e. Historical and bibliographical notes (Spanish) (Bol. Acad. Cien. Fis. Mat. Nat. 11(1948)), with 27 chapters on 250 pages, which contains more information on π and e than has ever before been collected in one place; Lessons on Infinitesimal Analysis (Caracas 1943, 606 pp.) (Spanish) containing material from courses in analysis at UCV during his first three or four years there; and Bibliography of Euclid, Archimedes, Newton (Acad. Cien. Fis. Mat. Nat., Caracas 1963, 163 pp.) (Spanish) which was also done in the 19th century.
Many mathematicians are interested in recreational mathematics. Duarte also contributed to that part of mathematics and proposed problems and solutions to the American Mathematical Monthly for several years, and also to the journal Ciencia y Ingenieria (Science and Engineering) published in Mérida. *SAU
1990 John Stewart Bell FRS (28 June 1928 – 1 October 1990) was a physicist from Northern Ireland (Ulster), and the originator of Bell's theorem, a significant theorem in quantum physics regarding hidden variable theories.*Wik
1996 Herbert Karl Johannes Seifert (May 27, 1907– October 1, 1996) was a German mathematician known for his work in topology.
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell



No comments:
Post a Comment