Houses and Utilities / Why it Can't be Done

By the time they reach high school, most students have encountered the problem of connecting the three houses to three utilities stated below:

Given three houses, A, B, and C; and three utilities, E, G, and W draw a connection from each utility to each house without the lines crossing. (The pretty image above came from the Math Forum web site, but I had already written my solution using A, B, and C so ... )


Although the problem usually comes with a location of the houses and utilities, such as the picture at right, they may actually be placed anywhere on a plane, or a sphere, and the problem is still the same.

A brief history of the game is taken from a note from David Singmaster,
Gas, Water and Electricity. Dudeney's Amusements in Mathematics (AM)(1917) describes this as being 'as old as the hills', but {this was the} earliest known reference until I found Dudeney's column in Strand Magazine 46 (Jul 1913) 110, but this still
says: "It is much older than electric lighting, or even gas ...."
In Sam Loyd and His Puzzles (1928), Sam Loyd Jr says he brought out the puzzle about 1900. Dudeney's Strand column says he has recently had four letters from the US about it. {Loyd was a US puzzle writer, Dudeney was in the UK)

Most students have tried this so often that they feel certain it is really not possible. Below I will try to provide two very different explanations as to why it is impossible to draw the figure on a plane or sphere.

A proof using the Jordan Curve Theorem

If we ignore, for a moment, the water plant and house C, however we place the utilities and houses A and B it should seem clear that G must connect to A and B, and E must connect to A and B also, and so a circuit GAEB must be formed from G to A to E to B. The Jordan Curve theorem says (in more formal language) that a closed curve, such as the circuit GAEB divides the plane (and the sphere) into two regions, we can call them the inside and the outside for our informal explanation.
Now what happens when we wish to place w, the water plant, on our picture. It could be inside, or outside. We will assume first that it lies inside the curve GAEB. and when it is connected to A and B, as shown at right, it will divide the inside into two smaller regions, which we will call inside1 (inside GBWA) and inside2(inside BWAE).
Now all we have to do is find a place for house C and we are done. House C could be placed in the outside region, but from there it could not be connected to W without crossing. House C could be placed in inside1, but from there it could not be connected to E without a crossing. Or we could place house C in inside2, but from there it cannot be connected to G without a crossing. We have shown that if W is placed inside, there is no way to place C without a crossing. The other place to put W is in the outside, but a similar proof will show that C cannot be connected then either. Can you complete the proof?
If we visualize the graph above as being on a sphere (think of the Earth), there is no loss of generality if we assume that points G, B, E, and A all lie on the equator. If W is placed in the Northern Hemisphere, or in the Southern, the picture, and the proof, is exactly the same.

A Proof Using Euler’s Theorem for Planer Graphs

Euler’s famous theorem says that in any planer graph (one that can be drawn without crossings) the relationship between vertices, V, edges, E, and faces, F, obeys the relationship V + F = E + 2. Let’s assume that in spite of all our efforts there really is a way to connect the vertices with non-crossing edges. Then there would be a planer graph with nine edges (E=9) and six vertices (V=6) . Using these two values in Euler’s equation we come to the conclusion that the number of faces, F, must be the solution to 6 + F = 9 + 2. That means there will be five faces to the plane figure.
So what is wrong with that? To answer that question we need to take a small diversion and look at some relationships in planer graphs in general. We will illustrate our point with the simple planer graph at the right, which has four faces and seven edges.
One way to count the edges would be to count the number of edges on each face. For example, Face 1 has 3 edges, face 2 has 4 edges, face 3 has 3 edges, and face 4 which goes all around the other three, has four edges. Notice that when we add all these up we get 4+3+4+3 = 14, but there are only 7 edges. Since each edge joins two faces, when we count the edges on the faces, we will get twice the number of edges as actually exist. Written algebraically this would be which just says that if you add up the number of edges on each face, you get twice the number of edges that really exist. So 2E/F would give us the average number of edges on the faces of a planer Graph. Now we are ready to use this idea of the average number of edges on a face to conclude our original proof. Remember that we found that if a planer graph was possible for the electricity problem, that there would have to be 5 faces on it, but we also knew it had 9 edges. So the average number of edges on each face, 2E/F will be 2(9)/5 = 3.6. But remember what the faces looked like in our problem; each face was created by at least four edges, utility to house to utility to house and back to utility. No face in this graph can have less than four edges, so an average of 3.6 is impossible, and we are forced to admit that no such planer graph can exist.
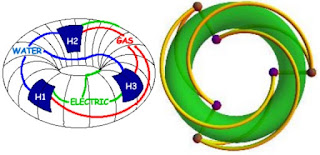
But on Some Shapes, It is Possible.

A torus is the mathematical name for a shape like a doughnut or inner tube from automobile tire. Can you convince yourself that the connections can be made without crossing on such a solid? Here is an illustration from Alexander Bogomolny's wonderful "Cut the Knot" Web site.

Can it be done on a Mobius’ Strip?

I should add here that this graph, called K_3,3 in graph theory is part of a famous 1929 proof by Kuratowski which bears his name that shows that ANY graph that is NOT planer has a subgraph which is either K_3,3 or K₅ (think of a pentagon with a pentagram drawn inside it).

Chains of Sums of Squares of Digits

I've always been fascinated by things like the Kaprekar Numbers and the orbits and absorbing states of number operations that seem to border on the edge of chaos and fractals.
Thinking along those lines this morning I decided to explore what happens when you sum the squares of the digits of a number, and then iterate that process on the results.

After a little while I convinced myself that the process would be bounded (no three digit number produces a number larger than three digits for example, in fact no number less than twelve digits would exceed 1000  on the first step of this process). This would force there to be either cycles or absorbing numbers, but would there be one, or many, and what kind of cycles would be generated, if any.

It didn't take long to figure out that one would be an absorbing state for any number that had a single unit and the rest zeros, 1, 10, 100 would all be absorbed by one; but also numbers like 7, 13, 31 70, 103, 130, 301, 700 and all permutations of the numbers that were absorbed more. Were there more? Yes 19 ,23, 28, 68, 44, 49, and of course 94, 91, 82, 32 and 68 would also be absorbed into one.


Other numbers jumped into a cycle that included four:
4 --- 16 --- 37--- 58 --- 89 --- 145 --- 42 --- 20 --- 4

Five took a few steps to find the cycle, then jumps in at 89:

5 --- 25 --- 29 --- 85 --- 89 --- 145 --- .... 4

6 found it's way to fifty, and then twenty-five and joined five's path to the same cycle: 6 --- 36 --- 45 --- 41 --- 17 --- 50 --- 25 ...... 4.

But 7 quickly found it's way to one via, 7 --- 49 --- 97 --- 130 --- 10 --- 1
Now I wondered if this were the fate of all numbers, to proceed along a path to either the cycle which contained four, or the absorption of one.

I begin hoping for exceptions, but found none below 1000. And that would mean that any number up to 1,000,000,000,000 would, go to a number less than 1000, and subsequently to either the absorbing one, or the cycle through four.

I couldn't find any thing about this sequence on line so I can't give any previous history before my little experiment. Perhaps I've stumbled across a new item. Anyway, Enjoy.

Addendum: David Brooks was kind enough to write me and inform me that those numbers which are absorbed by one are called "Happy Numbers", and they actually have an in-depth page on them about Wikipedia.

It includes :
The happy numbers below 500 are:

1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496 (sequence A007770 in OEIS).

A happy prime is a number that is both happy and prime. The happy primes below 500 are

7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409, 487 (sequence A035497 in OEIS).


As of 2010, the largest known happy prime is 2^{42643801}-1 (Mersenne prime). Its decimal expansion has 12,837,064 digits.

There are even Happy Pythagorean Triples, with all side lengths that are happy numbers. One is (700, 3465, 3535).

A Similar approach may be used with the sum of cubes of the digits, and there are also absorbing ones, as well as other absorbing states, but also a larger collection of cycling states possible.

Regarding the History, it seems little is known. Happy numbers were brought to the attention of Reg Allenby (a British author and Senior Lecturer in pure mathematics at Leeds University) by his daughter, who had learned of them at school. However, they "may have originated in Russia" according to Richard Guy in Unsolved Problems in Number Theory (3rd ed.)(Perhaps they should be called "счастливые номера")

The numbers have, it appears wove themselves into the mathematical/scientific underground (without my apparent notice) and in the 2007 Doctor Who episode "42", a sequence of happy primes (313, 331, 367, 379) is used as a code for unlocking a sealed door on a spaceship about to collide with a sun. When the Doctor learns that nobody on the spaceship besides himself has heard of happy numbers, he asks, "Don't they teach recreational mathematics anymore?"
Also, the contestants in the 2012 University Challenge final were asked to identify a sequence of numbers as happy primes in a picture round. (Ahh Jeremy Paxman you would have stumped me.)

So Thanks to David, and so many people who have stumbled across this before me.

A Couple of Nice Extensions of the Median Properties

One of the common topics in HS Geometry is to expose students to the triangle concurrency theorems, and in particular the fact that the medians of a triangle intersect in a single point that breaks each median in a ratio of 2:1.

As student's proceed through the years of HS, there are a couple of nice extensions that I find pleasing to expose students to. Others may enjoy sharing them with their students as well.

Added 2015  I just noticed a nice post on a curiously sweet property of the  medians in a post from Alex Bogomolny at Cut-The-Knot.  I will just give a teaser of it here, and you can follow the link to Alex's complete proof.

Amazingly, the sum of the reciprocals of the odd numbered in-radii is equal to the sum of the reciprocals of the even numbered in-radii.
  $\frac{1}{r_1} + \frac {1}{r_3} + \frac {1}{r_5} = \frac{1}{r_2} + \frac {1}{r_4} + \frac {1}{r_6}$

  Commandino's Theorem.
If you use the tetrahedron as a generalization of the triangle into three-space, then the four lines from each vertex to the centroid of the opposite faces (where the medians of that triangular face intersect) then these four medial segments also share a common intersection. In this case the ratio of the two parts into which it divides the segment is 3:1. (I usually make the extra emphasis, 2:1 in 2-D; 3:1 in 3-D and suggest that if there was a closed 4-D simplex the medial segments from the vertex to the centroid of the tetrahedral bases would be divided 4:1 by a common intersection, although I haven't proven that.)

Commandino is remembered for translating many ancient texts. He presented this theorem in 1565 as Prop. 17 in his De Centro Gravitates Solidorum on Centers of Gravity.

I came across another interesting extension in a January 1951 "Mathematical Miscellanea" edited by Phillip S. Jones. The article contained a contribution by John Satterly of the University of Toronto on a type of cevian that he called "Nedians" which I wrote about a little over a year ago. [My personal choice, since the "med" root is for the middle, would have just been to call them n-dians, but I'm sure that would have had a cultural backlash.]

Instead of dividing each point on the triangles legs at the point 1/2 way between them, suppose we marked a point 1/3 (or 1/n) of the way.

Professor Satterly showed that the sum of the squares of the nedians would be times the sum of the squares of the sides of the original triangle. Notice that when n=2, this reduces to 3/4, the ratio given and proved for the medians in an earlier blog.

Professor Satterly also stated that the Nedian triangle will have an area of times the area of ABC. Note that for the median, or 2-nedian, the area diminishes to zero since the three medians intersect in a single point.

Exploring these constructions a little more, I came up with a few more properties that were not in the article. For example, the perpendicular distance from the three vertices of the nedian triangle to any side of ABC will equal the altitude of ABC to that same side. [I call these the sub-altitudes (dotted red in the image below)]

The shortest sub-altitude will be , while the next longer one will be and the longest will be .   In the example where the points are located 1/3 of the way along the side, the three sub-altitudes will be 1/7 h, 2/7 h, and 4/7 h.  This property applies to the altitude and sub-altitudes to each base.

I also observed that that each nedian is partitioned into three parts whose lengths, in order from the vertex to the opposite side, are
 .

For the 3-nedians in the image, for example, the nedian CF is partitioned so that CJ is 3/7of CF; JL is 3/7 of CF; and LF is 1/7 of LF. A similar partition holds for the other two 3-nedians AD and BE. In a 4-nedian, the partitions would be 4/14, 8/13, and 1/14.

Some or all of these are probably well within the range of a talented HS student.  I hope they are of interest to teachers and students.  Enjoy

Really Nice Problem from Greg Ross

Just came across a really neat problem for introducing the Pigeon Hole problem to High School Algebra Students with some deep reasoning about the midpoint of a line segment.

It's all posted, with answers at Greg Ross' Futility closet (which should be a regular read for math teachers because he has wonderful ideas related to mathematical ideas and number relations)

A discovery prelude might be to ask students during mid-point problems to see if they can find two, three, n points placed on the grid where no midpoint will lie on an intersection of grid lines.  Lots of practice finding midpoints and  hopefully they can discover something of parity relationships that produce intersection.  Would seem more ready for approach to a proof. 

Other ideas? 

A Brief History of the River Crossing Problem

Recently reading through some new math blogging educators on Sue Van Hattum's web page, Math Mama Writes, and one used variations of the "River Crossing" problem to link algebra to their middle school student's arithmetic learning and reminded me that I wanted to gather together my notes on the history of this great old problem.

For those who actually have not heard of the river crossing problem, a common version is something like this example from a rather nice Wikipedia posting:

The jealous husbands problem, in which three married couples must cross a river using a boat which can hold at most two people, subject to the constraint that no woman can be in the presence of another man unless her husband is also present.

David Singmaster, one of the foremost (if not THE foremost) historian on the history of recreational mathematics credits the 9th Century Alcuin of York, an English scholar, ecclesiastic, poet and teacher from York, Northumbria. He was born around 735 and became friend and adviser to Charlemagne and the leading teacher at his court.
His Propositiones ad Acuendos Juvenes (Problems to sharpen the young contains the first written record of River Crossing Problems, apparently of three versions. Wikipedia lists the fox, goose and bag of beans puzzle and the Jealous Husbands problem above. (If you know the third version in his book, I would love to be informed).

The book also includes the first Explorer's Problem; first Division of Casks; first
Apple-sellers' Problem; first Collecting Stones; unusual solution of
Posthumous Twins Problem; first Three Odds Make an Even; and the first Strange
Families problem.

Professor Singmaster notes Pacioli's 1500 De Viribus has the next essential variation in the game, a river crossing that contains boats to hold more than two people. Then a few years later (1556), Tartaglia's General Trattato introduces the first River Crossing with four
couples. In his Science News blog, Ivars Petersen adds "With four or more couples, however, it's impossible to accomplish the crossings under the required conditions."
Several hundred years later, In volume 1 of Eduard Lucas' Recreations Mathematiques he Gives De Fontenay's idea of couples crossing a river with an island. This would solve the four-couple Jealous Husbands problem. Lucas is also well remembered for his Towers of Hanoi Puzzle (briefly referenced in the picture at top with the tower of discs, and perhaps the turtle is a reference to Lo Shu and Magic Squares) and a Fibonacci like series that bears his name.

Today the forms of the puzzle have spread to reflect more modern additions to cultures. In the 19th Century Cannibals and Missionaries were a popular subject. A warfare version enters in this version from, I believe, a Russian version in the early 20th Century :

A detachment of soldiers must cross a river. The bridge is broken, and the river is deep. The officer in charge spots two boys playing in a rowboat by the shore. The boat is so tiny, however, that it can only hold two boys or one soldier. All the soldiers succeed in crossing the river in the boat. How?

And finally, this tongue-in-cheek quote from Ivars Petersen's Science News Article:

"One must be a little careful with some of these problems, as past cultures were often blatantly sexist or racist," Singmaster warns. "But such problems also show what the culture was like. . . . The river crossing problem of the jealous husbands is quite sexist and transforms into masters and servants, which is classist, then into missionaries and cannibals, which is racist. With such problems, you can offend everybody!"

Just to show a little of the popularity of these puzzles, I recently found a web page, Puzzle Museum, that had images of a Turnbridge Ware box of Puzzles sold by Rudolph Ackerman in the first quarter of the 19th Century. Inside one of the envelopes are cut-outs for the Wolf/goat/Seed and Jealous Husbands river crossing problems. Two other games were included, the Josephus (Turks and Christians count-out game) problem, and one of the dissected Cross.

Charles Dodgson (Lewis Carroll) often sent puzzles to his child-friends and included the river crossing problem with Fox, Goose, and Corn to young Jessie Sinclair. His interest in the problem seems to include the creation of an original variation on the problem, although there seems to be no direct evidence that he first created it.
His version is varioulsy called "The Captive Queen", or just the tower problem. Here is one version:

A captive queen and her son and daughter were shut up in the top room of a very high tower. Outside their window was a pulley with a rope around it, and a basket fastened to each end of the rope of equal weight. They managed to escape with the help of this and a weight they found in the room, quite safely. It would have been dangerous for any of them to come down if they weighed 15 lbs more than the content of the other basket, for they would do so too quick, and they also managed not to weigh less either.

The one basket coming down would naturally of course draw the other basket up.

The queen weighed 195 lbs, daughter 105, son 90, and the weight 75 lbs.

How did they all escape safely?

About three years after I wrote the above, Jim Wilder posted a version I had overlooked, involving a ball of twine.

This is from a wonderful collection of puzzles from a mathematician who has undoubtedly sold more mathematical puzzle books than anyone in the world. It is a Wonderful book to keep on the desk for a (sometimes) quick challenge.




River crossing problems seem to show across cultures. In Africa Counts: Number and Pattern in African Cultures, Claudia Zaslavsky mentions a version told by Kpelle children in Liberia in which a man must ferry a leopard, a goat, and a bunch of Cassava leaves. No period or origin of the puzzle is given, and the similarity to the fox, goat, and beans in Alcuin's problem makes one wonder if one influenced the other.

meetasengupta @Meetasengupta tweeted that "Bengali--> Bagh-pan-chhagol (tiger, leaves, goat) version too. Punjabis had a lovers version-I've forgotten! 

Over the years I have come across several tongue-in-cheek solutions to river crossing type problems, so here are a couple of nice examples:
The first is from the wonderful XKCD site:

The Second is a business approach from Dilbert.Com:

If you  have other notes, information, or references to the history of these problems, I would love to hear from you. 

The B-2 Formula

Going through some old class notes from a few years ago and rememered this old post from 2008....
Hope all these kids are doing well today.
---------------------------------------------------------------------------------------------

In my B2 Pre-calc class today, we re-discovered a theorem about Pascal's triangle that I had not known. It began, appropriately enough, with a question Jacob C. asked about dealing cards from a standard deck; "How many 13 card hands can be dealt that contain exactly two suits. " As we were working through the problem, I began by attacking the somewhat easier problem, "how many hands can be dealt with only hearts and diamonds, but at least one of each." We began writing out the possibilities of 12 hearts, 1 diamond plus 11 hearts two diamonds ..etc To make life easy, for this short while let’s let (n,r) mean “n choose r” , the combinations of n things taken r at a time. So we needed to find (13,1)(13,12) for the first part, 12 hearts and 1 diamond. Then we needed to add on (13,2)(13,11) + (13,3)(13,10)…. And all the way down to (13,1)(13,12). One of the clever ones quickly realized that each of these pairs were just the same number due to the symmetry of Pascal's triangle, and so we were really looking for (13,1)² + (13,2)²... etc. While some of the kids were adding these on their calculators, I wrote out several lines of the arithmetic triangle and began to write the sums of squares on the right....

As I wrote the totals of each row, 1, 2, 6, 20, 70.. it struck me that they were all the center number of an even numbered row, (2n,n). I remembered them from working with Catalan’s Numbers (another cool pattern that shows up in Pascal’s triangle). About the time the first students were coming up with an answer, I asked them to check (26, 13) and compare it to the answer they got for the actual squares of the thirteenth row…

Close, but not right, was the reply.... huh??? … , oh yeah, we had avoided the case of (13,0) and (13,13) because we wanted to ignore the case where all were hears or all were diamonds, so the answer to our mini-problem was (26,13) - 2; and the only thing needed to solve the original problem was to multiply by 6, to account for all the ways we could pick two suits to be in the hand out of the four possible suits.

When I showed them the result, and we checked a couple of more cases to be more sure, I admitted that I had never seen this theorem. One kid suggests it should be a test question… I countered with, “and extra credit for the person who comes up with the best name for it. Several played to my ego, “Ballew’s theorem, of course!” but then they thought they might deserve partial credit, and hence the name, B-2 theorem, at the top.

Unfortunately, we were not the first to stumble across this little gem. I haven’t had time to chase it down fully, but it may actually date back to the Chinese around the 12th century. So fame and fortune will have to wait, but when you walk in the footsteps of greatness, you’re taking pretty big steps; so congratulations class, I’m proud of you, and it will always be the B-2 theorem when I teach it. Dennis was going to send me a class picture we took on his phone, so if it turns out, I will add that later,

While I was searching for the history of the sum of the binomial coefficients, I came across another place where the triangle is related to squares. One of those theorems we teach when we get to sequence and series in high school is the sum of the integers, 1 + 2 + 3 + … + n, and the sum of the squares of the integers, 1² + 2² + 3² + ….. + n².
Usually we present the formula for this last without proof since it occurs before they are introduced to inductive proofs. As I was researching I came across this neat little relation to the arithmetic triangles. To find the sum of the squares of the first ten integers, just go down to 10 at (10,1) and turn right and follow the diagonal down two numbers to (12,3) and add this to the number on the diagonal above it (11,3), the sum of 220 + 165 = 385 which is the same as 1² + 2² + … + 10²

In general you can find

And I think they can accept that as evidence, at least until we get to inductive proofs.

A Neat interconnection in Math

Just came across some old notes I used to use for entertaining diversions in Pre-calc a dozen or so years ago. My notes say I got these ideas from something by Richard Guy (I know that leaves it pretty loose) that was also related to Friezes in math, but I only used a small bit of what they said on that.

The first idea is the idea of a unimodular rule, which I had not encountered anywhere else. It was the idea of a diamond of numbers, as below, in which B*C– A*D = 1

   A
B   C
   D
They showed that if you start with a row of zeros, follow with a row of zeros on the second row, and add particular types of periodic sequences in the next row, you can continue to construct more rows by filling in with the unimodular rule. For example if we pick something as simple as 13122 we can continue to apply the unimodular rule in each new row, and eventually we are forced by to another row of ones with a row of zeros below it.
  0   0   0   0   0   0   0   0   0 ….
1   1   1   1   1   1   1   1   1   1 ….
  1   3   1   2   2   1   3   1   2   2

Our next row would have to start with 2, since 3*1-1*D = 1 solves for 2.
Continuing the process we get
   0   0   0   0   0   0   0   0   0 ….
1    1   1   1   1   1   1   1    1   1 ….
  1     3   1   2   2   1   3   1   2   2
2    2   1   3   1   2   2   1   3   1


Notice that we are (in this simple case) repeating the previous sequence translated to the right a bit. The next lines as you should see, forces all terms to be ones, and the final line produces all zeros.
Here is an example I believe I got from the original paper.

This was has been sectioned to illustrate the fact that these friezes also have a glide reflection element in the pattern.

And now the pretty part; but before you proceed you might try to pick a four to six digit sequence to see if it works. Some do, but some don’t.


Pausing for thoughts and experimentation....


Dum de dum dum….




OK, ready to go on?


The pretty part about this experience is that there is an easy, geometric way to find sequences of any length that you want and they work, They ALWAYS work .
My notes say this part was a contribution from that great Geometrician, John Conway, a frequent collaborator with Guy.
The Geometry is based on triangulations of a polygon. My sequence above, 1 3 1 2 2 , is based on a triangulation of a pentagon. You simply draw a polygon and construct diagonals in it to divide it into triangles. Then walk around the vertices of the triangle and count the number of triangles that contain that vertex. The numbers you get in order around the vertices consist of a sequence of n numbers (the same as the number of vertices in your n-gon) that are a working sequence in creating a frieze pattern.

Here is my triangulation used to create the sequence 1 3 1 2 2

And that, in my mind, is a neat and unexpected connection. If it counts triangulations of a convex polygon, then it works in the third row of the frieze, and if it works in the frieze, it is the triangulation of a convex polygon.  I have no idea how John Conway may have made the connection between these two seemingly different mathematical objects, but love the result.
The number of rows in your frieze is always one more than the n of your n-gon.