 |
| Steiner eircumellipse *wolfram alpha |
Scientific discovery consists in the interpretation for our own convenience of a system of existence which has been made with no eye to our convenience at all.
~Norbert Wiener
The 77th day of the year; 77 is the only number less than 100 with a multiplicative persistence of 4. Can you find the next? (Multiply all the digits of a number n, repeating with the product until a single digit is obtained. The number of steps required is known as the multiplicative persistence, and the final digit obtained is called the multiplicative digital root of n.) There is not another year day that will have a multiplicative persistence greater than four. [7x7=49, 4x9=36, 3x6=18, 1x8=8]
772 is the smallest square number that can be the sum of consecutive squares greater than 1, \(sum_{k=18}^{28}k^2 = 77^2\)
The concatenation of all palindromes from one up to 77 is prime.
77 is equal to the sum of three consecutive squares, \(4^2 + 5^2 + 6^2= 77\) and also the sum of the first 8 primes. *Prime Curios
EVENTS
1973 Comet Kohoutek, formally designated C/1973 E1, 1973 XII, and 1973f, was first discovered on this date while examining photographic plates taken on 7 March 1973 by Czech astronomer Luboš Kohoutek. It attained perihelion on 28 December that same year. Will not be back for a really, really long time.
In 1987, the discovery of "high-temperature" superconductivity was announced to thousands of scientists at a packed meeting of the American Physical Society in New York City. The phenomenon, discovered 1911, was at first known to occur at only 4 degrees above absolute zero, when all electrical resistance in a metal sample disappeared. In 1986, researchers discovered a ceramic material that was a superconductor at a temperature of more than 30 degrees above absolute zero. When published in September of that year, that news stirred the wider scientific community into action. By the time of the APS meeting, further discoveries had been made. The scene of excitement at the meeting was dubbed the "Woodstock of Physics." *TIS
1990 The Mathematische Gesellschaft, the world’s oldest existing mathematical society (founded 1690) began a seven day meeting in Hamburg to celebrate its third centenary. *VFR
2010 It was announced that Grigori Yakovlevich Perelman had met the criteria to receive the first Clay Millennium Prize for resolution of the Poincaré conjecture. On 1 July 2010, he turned down the prize of one million dollars, saying that he considers his contribution to proving the Poincaré conjecture to be no greater than that of Richard Hamilton, who introduced the theory of Ricci flow with the aim of attacking the geometrization conjecture. *Wik
2011 The Pluto-bound New Horizons spacecraft flew past Uranus’ orbit at about 6 p.m. EDT, 1.8 billion miles from Earth. New Horizons is now well over halfway through its journey to Pluto. Motoring along at 57,9000 km/hr (36,000 mph), it will travel more than 4.8 billion km (3 billion miles) to fly past Pluto and its moons Nix, Hydra and Charon in July 2015.The next planetary milestone for New Horizons will be the orbit of Neptune, which it crosses on Aug. 25, 2014, exactly 25 years after Voyager 2 made its historic exploration of that giant planet. *Universe Today (Hat tip to David Dickinson@Astroguyz
BIRTHS
1640 Philippe de La Hire (or Lahire or Phillipe de La Hire) (March 18, 1640 – April 21, 1718) was a French mathematician and astronomer. According to Bernard le Bovier de Fontenelle he was an "academy unto himself". La Hire wrote on graphical methods, 1673; on conic sections, 1685; a treatise on epicycloids, 1694; one on roulettes, 1702; and, lastly, another on conchoids, 1708. His works on conic sections and epicycloids were founded on the teaching of Desargues, of whom he was his favourite pupil. He also translated the essay of Manuel Moschopulus on magic squares, and collected many of the theorems on them which were previously known; this was published in 1705. He also published a set of astronomical tables in 1702. La Hire's work also extended to descriptive zoology, the study of respiration, and physiological optics.
Two of his sons were also notable for their scientific achievements: Gabriel-Philippe de La Hire (1677–1719), mathematician, and Jean-Nicolas de La Hire (1685–1727), botanist.
The mountain Mons La Hire on the Moon is named for him. *Wik He was also the first to find the arc length of the cardioid in 1708.
1690 Christian Goldbach (18 Mar 1690, 20 Nov 1764) Russian mathematician whose contributions to number theory include Goldbach's conjecture, formulated in a letter to Leonhard Euler dated 7 Jul 1742. Stated in modern terms it proposes that: "Every even natural number greater than 2 is equal to the sum of two prime numbers." It has been checked by computer for vast numbers - up to at least 4 x 1014 - but still remains unproved. Goldbach made another conjecture that every odd number is the sum of three primes, on which Vinogradov made progress in 1937. (It has been checked by computer for vast numbers, but remains unproved.) Goldbach also studied infinite sums, the theory of curves and the theory of equations. *TIS
1796 Jakob Steiner (18 Mar 1796; 1 Apr 1863 at age 67) Swiss mathematician who was one of the greatest, contributors to projective geometry. He discovered the Steiner surface which has a double infinity of conic sections on it. The Steiner theorem states that the two pencils by which a conic is projected from two of its points are projectively related. He is also known for the Poncelet-Steiner theorem which shows that only one given circle and a straight edge are required for Euclidean constructions. His work included conic sections and surfaces, the theory of second-degree surfaces and centre-of-gravity problems. He developed the principle of symmetrization (1840-41). In 1848 he ws the first to define various polar curves with respect to a given curve, and introduced the “Steiner Curves.” *TIS
1839 Joseph Émile Barbier (18 March 1839 in St Hilaire-Cottes, Pas-de-Calais, France - 28 Jan 1889 in St Genest, Loire, France)
He was offered a post at the Paris Observatory by Le Verrier and Barbier left Nice to begin work as an assistant astronomer. For a few years he applied his undoubted genius to problems of astronomy. He proved a skilled observer, a talented calculator and he used his brilliant ideas to devise a new type of thermometer. He made many contributions to astronomy while at the observatory but his talents in mathematics were also to the fore and he looked at problems in a wide range of mathematical topics in addition to his astronomy work.
As time went by, however, Barbier's behaviour became more and more peculiar. He was clearly becoming unstable and exhibited the fine line between genius and mental problems which are relatively common. He left the Paris Observatory in 1865 after only a few years of working there. He tried to join a religious order but then severed all contacts with his friends and associates. Nothing more was heard of him for the next fifteen years until he was discovered by Bertrand in an asylum in Charenton-St-Maurice in 1880.
Bertrand discovered that although Barbier was clearly unstable mentally, he was still able to make superb original contributions to mathematics. He encouraged Barbier to return to scientific writing and, although he never recovered his sanity, he wrote many excellent and original mathematical papers. Bertrand, as Secretary to the Académie des Sciences, was able to find a small source of income for Barbier from a foundation which was associated with the Académie. Barbier, although mentally unstable, was a gentle person and it was seen that, with his small income, it was possible for him to live in the community. This was arranged and Barbier spent his last few years in much more pleasant surroundings.
Barbier's early work, while at the Observatory, consists of over twenty memoirs and reports. These cover topics such as spherical geometry and spherical trigonometry. We mentioned above his work with devising a new type of thermometer and Barbier wrote on this as well as on other aspects of instruments. He also wrote on probability and calculus.
After he was encouraged to undertake research in mathematics again by Bertrand, Barbier wrote over ten articles between the years 1882 and 1887. These were entirely on mathematical topics and he made worthwhile contributions to the study of polyhedra, integral calculus and number theory. He is remembered for Barbier's theorem, nicely explained here by Alex Bogomolny.*SAU
1870 Agnes Sime Baxter (Hill) (18 March 1870 – 9 March 1917) was a Canadian-born mathematician. She studied at Dalhousie University, receiving her BA in 1891, and her MA in 1892. She received her Ph.D. from Cornell University in 1895; her dissertation was “On Abelian integrals, a resume of Neumann’s ‘Abelsche Integrele’ with comments and applications." *Wik
1891 Walter Andrew Shewhart (March 18, 1891 - March 11, 1967) was an American physicist, engineer and statistician, sometimes known as the father of statistical quality control.
W. Edwards Deming said of him, "As a statistician, he was, like so many of the rest of us, self-taught, on a good background of physics and mathematics. "
His more conventional work led him to formulate the statistical idea of tolerance intervals and to propose his data presentation rules, which are listed below:
Data have no meaning apart from their context.
Data contain both signal and noise. To be able to extract information, one must separate the signal from the noise within the data.
Walter Shewhart visited India in 1947-48 under the sponsorship of P. C. Mahalanobis of the Indian Statistical Institute. Shewhart toured the country, held conferences and stimulated interest in statistical quality control among Indian industrialists
*SAU
1911 Walter Ledermann (18 March 1911 in Berlin, Germany - 22 May 2009 in London, England) graduated from Berlin but was forced to leave Germany in 1933 to avoid Nazi persecution. He came to St Andrews and studied under Turnbull. He worked at Dundee and St Andrews until after World War II when he moved to Manchester and then to the University of Sussex. He is especially known for his work in homology, group theory and number theory. *SAU
1928 Lennart Axel Edvard Carleson (18 March 1928 in Stockholm, Sweden - ) is a Swedish mathematician who solved one of the most important problems in the theory of Fourier series. He was director of the Mittag-Leffler Institute, Stockholm, from 1968 to 1984, during which time he built the Institute from a small base into one of the leading mathematical research institutes in the world.*SAU
DEATHS
In formal logic, De Morgan's laws are rules relating the logical operators "and" and "or" in terms of each other via negation. With two operands A and B:
- NOT (P AND Q) = (NOT P) OR (NOT Q)
- NOT (P OR Q) = (NOT P) AND (NOT Q)
"The negation of a conjunction is the disjunction of the negations." and*Wik
"The negation of a disjunction is the conjunction of the negations."
When he defined and introduced the term "mathematical induction" (1838), he gave the process a rigorous basis and clarity that it had previously lacked. He originated the use of the slash to represent fractions, as in 1/5 or 3/7. In Trigonometry and Double Algebra (1849) he gave a geometric interpretation of complex numbers. *TIS A nice blog about De Morgan's life and relationships is at The Renaissance Mathematicus.
Teachers might give students the opportunity to find the date of his birth using De Morgan's own clues; “I was x years old in the year x2” *VFR
1907 Pierre-Eugène-Marcellin Berthelot (27 Oct 1827, 18 Mar 1907 at age 79) was a French chemist and science historian and government official whose creative thought and work significantly influenced the development of chemistry in the late 19th century. He helped to found the study of thermochemistry, introduced a standard method for determining the latent heat of steam, measured hundreds of heats of reactions and coined the words exothermic and endothermic. Berthelot systematically synthesized organic compounds, including some not found in nature. His syntheses of many fundamental organic compounds helped to destroy the classical division between organic and inorganic compounds. *TIS
1964 Norbert Wiener (26 Nov 1894; 18 Mar 1964) U.S. mathematician, who established the science of cybernetics, a term he coined, which is concerned with the common factors of control and communication in living organisms, automatic machines, and organizations. He attained international renown by formulating some of the most important contributions to mathematics in the 20th century. His work on generalised harmonic analysis and Tauberian theorems won the Bôcher Prize in 1933 when he received the prize
 from the American Mathematical Society for his memoir Tauberian theorems published in Annals of Mathematics in the previous year. His extraordinarily wide range of interests included stochastic processes, quantum theory and during WW II he worked on gunfire control. *TIS Cybernetics, published in 1948, was a major influence on later research into artificial intelligence. In the book, Wiener drew on World War II experiments with anti-aircraft systems that anticipated the course of enemy planes by interpreting radar images. Wiener also did extensive analysis of brain waves and explored the similarities between the human brain and a modern computing machine capable of memory association, choice, and decision making.*CHM (Wiener is somewhat revered as the ultimate absent-minded professor. An anecdote I used to share with my classes, almost certainly exaggerated, went something like this: Wiener had moved to a new address, and his wife knowing of his forgetfulness wrote a note with his new address and put it in his coat pocket. During the day struck by a mathematical muse he whipped out the piece of paper and scribbled notes on the back, then realizing his idea had been wrong, he tossed the piece of paper away and went about his day. In the afternoon he returned to his old house out of habit and coming up to the empty house remembered that he had moved, but not where. As he started to leave a young girl walked up and he stopped here. "Young lady, I am the famous mathematician Wiener. Do you know where I live?" The lass replied, "Yes, father, I'll show you the way home."... )
from the American Mathematical Society for his memoir Tauberian theorems published in Annals of Mathematics in the previous year. His extraordinarily wide range of interests included stochastic processes, quantum theory and during WW II he worked on gunfire control. *TIS Cybernetics, published in 1948, was a major influence on later research into artificial intelligence. In the book, Wiener drew on World War II experiments with anti-aircraft systems that anticipated the course of enemy planes by interpreting radar images. Wiener also did extensive analysis of brain waves and explored the similarities between the human brain and a modern computing machine capable of memory association, choice, and decision making.*CHM (Wiener is somewhat revered as the ultimate absent-minded professor. An anecdote I used to share with my classes, almost certainly exaggerated, went something like this: Wiener had moved to a new address, and his wife knowing of his forgetfulness wrote a note with his new address and put it in his coat pocket. During the day struck by a mathematical muse he whipped out the piece of paper and scribbled notes on the back, then realizing his idea had been wrong, he tossed the piece of paper away and went about his day. In the afternoon he returned to his old house out of habit and coming up to the empty house remembered that he had moved, but not where. As he started to leave a young girl walked up and he stopped here. "Young lady, I am the famous mathematician Wiener. Do you know where I live?" The lass replied, "Yes, father, I'll show you the way home."... )Wiener is buried in Vittum Hill Cemetery in Sandwich, Carroll County, New Hampshire, USA
reader Tom @umacf24 told me that "Before this guy, 'kyber' was an obscure Greek word for 'steering.' " (seems very appropriate root) Thanks Tom.
1989 Sir Harold Jeffreys (22 Apr 1891, 18 Mar 1989 at age 97)English astronomer, geophysicist and mathematician who had diverse scientific interests. In astronomy he proposed models for the structures of the outer planets, and studied the origin of the solar system. He calculated the surface temperatures of gas at less than -100°C, contradicting then accepted views of red-hot temperatures, but Jeffreys was shown to be correct when direct observations were made. In geophysics he researched the circulation of the atmosphere and earthquakes. Analyzing earthquake waves (1926), he became the first to claim that the core of the Earth is molten fluid. Jeffreys also contributed to the general theory of dynamics, aerodynamics, relativity theory and plant ecology.*TIS
2001 Dirk Polder (August 23, 1919, The Hague — March 18, 2001, Iran) was a Dutch physicist who, together with Hendrik Casimir, first predicted the existence of what today is known as the Casimir-Polder force, sometimes also referred to as the Casimir effect or Casimir force. He also worked on the similar topic of radiative heat transfer at nanoscale. *Wik
2013 Mary Ellen Rudin (born December 7, 1924, Hillsboro, Texas - March 18, 2013, Madison, Wisconsin) was an American mathematician.
Born Mary Ellen Estill, she attended the University of Texas, completing her B.A. in 1944 and her Ph.D. in 1949, under Robert Lee Moore. In 1953, she married the mathematician Walter Rudin. Following her mentor Moore, her research centers on point-set topology. She was appointed as Professor of Mathematics at the University of Wisconsin in 1971, and is currently a Professor Emerita there. She served as vice-president of the American Mathematical Society, 1980–1981. In 1984 she was selected to be a Noether Lecturer. She is an honorary member of the Hungarian Academy of Sciences (1995).
Rudin is best known in topology for her constructions of counterexamples to well-known conjectures. Most famously, she was the first to construct a Dowker space, thus disproving a conjecture of Dowker's that had stood, and helped drive topological research, for more than twenty years. She also proved the first Morita conjecture and a restricted version of the second. Her latest major result is a proof of Nikiel's conjecture. Rudin's Erdős number is 1.
"Reading the articles of Mary Ellen Rudin, studying them until there is no mystery takes hours and hours; but those hours are rewarded, the student obtains power to which few have access. They are not hard to read, they are just hard mathematics, that's all." (Steve Watson)
She lived in Madison, Wisconsin, in the Rudin House, a home designed by architect Frank Lloyd Wright, and died at the age of 88. *SAU
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbel

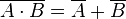
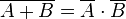
No comments:
Post a Comment