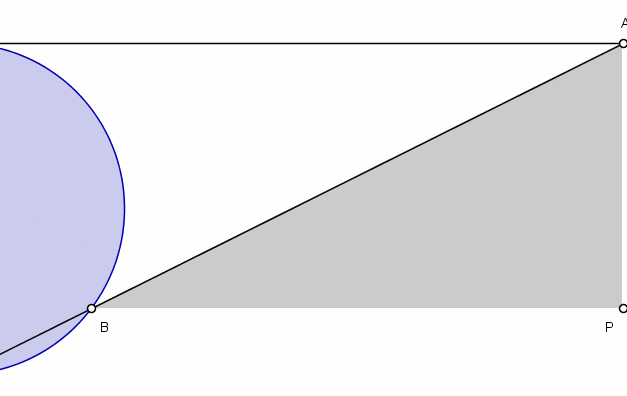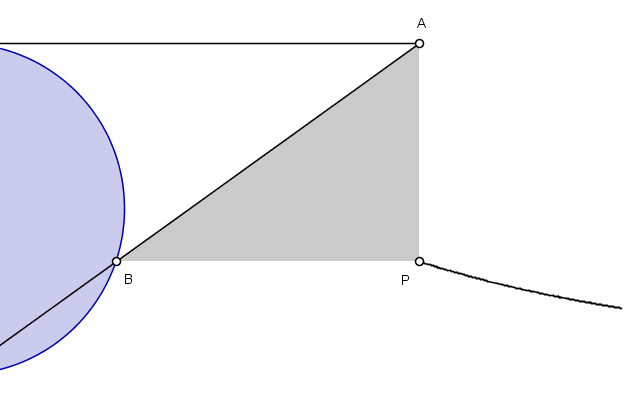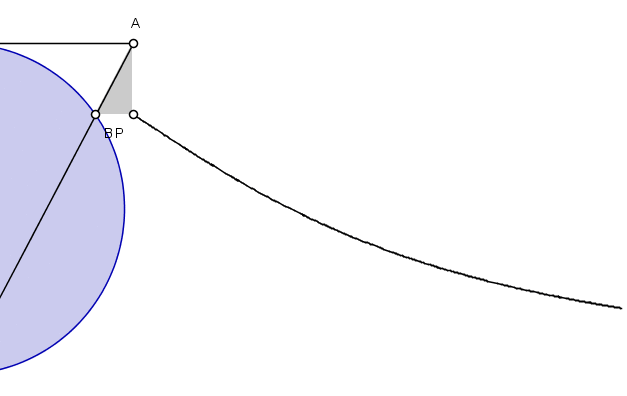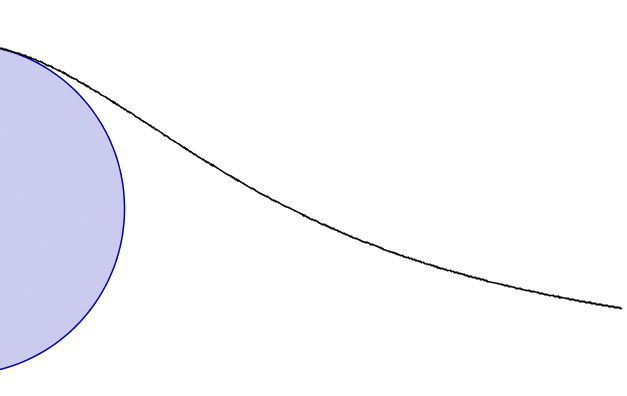
An animation showing the construction of the Witch of Agnesi, *Wik
Nature is never so admired as when she is understood.
~Bernard le Bovier de FontenelleThe 9th day of the year; of all the odd numbers in the Fibonacci sequence, none has a factor of nine. (students might search for the smallest odd prime number that is not a factor of any of the Fibonacci numbers)
8 and 9 (2^3 and 3^2) are the only consecutive powers of integers. The result, x^y -y^x = 1 has only one solution for x, y both greater than 1) conjectured in 1842 by Eugène Catalan, was proved in 2002 by Preda Mihăilescu.
If you wrote , e, and one under another, they all have a 9 in the 13th digit.
And *Jim Wilder@wilderlab tweeted, "9 can be written upside down and read the same in binary: 1001, or when written as shown in the photo."
And from Cliff Pickover @Pickover, the square of the nine digit rep unit produces an interesting number, 111,111,1112; = 12345678987654321 (You can do this with larger numbers but need to add zeros for carrys; 20202020202020202^2 =408121620242832363228242016120804) For Even more fun, try 10101010101010101^3
1621 J. WELLES (author of Sciographia, or the Art of Shadows,) writes to HENRY BRIGGS at MERTON COLLEGE in Oxford to offer help in the construction of logarithms for base ten. It appears that he assisted in the calculations for the Arithmetica Logarithmica. * Augustus De Morgan, Correspondence of scientific men of the seventeenth century ..., Volume 1
1639 In a letter to Frenicle, Descartes expressed the belief that an odd perfect number might exist. He had previously used the example of ps^2 where s = 3* 7 * 11*13 and p was a prime, and suggested that it could be made perfect if p were prime, and other values replaced some or all of 3, 7, 11, 13. So far, no one has found the replacements to make that happen, but no one has proved that an odd perfect number can not exist.
In 1643, Giovanni Riccioli first reported the phenomenon known as the Ashen Light of Venus. It is said to be a faint luminescence on the night side of the planet, similar in appearance to "earthshine" on the Moon, although not so bright. Ashen Light has been most often sighted when Venus was in the evening sky, when the evening terminator of the planet is toward the Earth. Studies have been attempted by several space missions, including Pioneer and the Russian Venera 11 and 12 landers. Still, the phenomenon remains sporadic and the explanation elusive. *TIS
1793 President George Washington watched as Jean-Pierre Blanchard soared over the Delaware River and into New Jersey skies, before finally landing in Deptford Township for the first hot air balloon flight and landing in North America’s history. *Kelly Roncace/South Jersey Times
In 1816, Sir Humphry Davy's safety lamp was first used in a coal mine. Deadly explosions had been a continual hazard caused by the flammable gas, methane, leaking out of the coal seams ignited by the flame of a miner's lamp. There had been previous attempts by others to make a safety lantern. Davy applied a scientific approach to determine the suitable fineness of wire gauze placed around the flame which would avoid ignition of flammable gas outside. He determined that the holes in the gauze should be less than 1/22 inch in diameter, and that the wire itself should be between 1/40 to 1/60 inch thick. Since the flame changed colour in the presence of methane, it also served as a warning to the miner to take protective action.*TIS
1839 Henderson announces first stellar parallax. *VFR The Scottish Astronomer Royal, Thomas Henderson, published the results of his measurement, the first made of a stellar parallax. He observed the star Alpha Centauri from the Cape of Good Hope, South America. (It is not visible from Britain.) His measurements were made in 1831-33. After that time, but before Henderson completed his calculations and published his results, both Friedrich Bessel and Friedrich Struve had been recognized as the first to make measurements of stellar parallax.*TIS

In 1901, the first application for a patent for Meccano was submitted, as "Improvements in toy or educational devices for children and young people. Known at first as "Mechanics Made Easy," this invention of Frank Hornby became a worldwide success. The British patent (No. 587) showed the familiar perforated strips, pulleys, axles, brackets and clips assembled as a model railway crane with tracks that had operating points. The patent was published on 30 Nov 1901.*TIS (In the U S these are called "Erector Sets")
1947 According to Claude Shannon, it was on this day that John Tukey sent a Bell Labs memo creating the term bit, as an acronym for "Binary Information Digit." *Wik
1956 The Soviet Union issued a stamp commemorating the tenth anniversary of the death of Alexei N. Krylov (1863–1945), mathematician and naval architect. [Scott #1792] *VFR
1972 Mariner 9 transmitted black and white pictures of Mars back to Earth using the first order (32, 6, 16) Reed-Muller code. See Chester J. Salwach, “Codes that detect and correct errors,” The College Mathematics Journal, 19(1988), 402–416. *VFR
A mosaic of Mariner 9 frames, taken during the spacecraft's first orbit of Mars, showed the south polar cap dimly through a great dust storm.
1991 After the Fullerenes discovery and Nobel Prize the session of the House of Lords entertained a question from Lord Errol of Hale as to "What steps the government was taking to encourage the use of Fullerines in science and industry?" The question prompted questions on what was a Fullerene, what shape did it have and finally, this brilliant exchange:
Lord Campbell of Alloway: "My Lords, what does it do?"
Lord Reay: "My Lords, it is thought that it may have several possible uses... All that is speculation. It may turn out to have no uses at all."
Earl Russell: "My Lords, can one say that it does nothing in particular, and does it very well." *Siobhan Roberts, King of Infinite Space
In 1998, two teams of international collaborations of scientists announced the discovery that galaxies are accelerating, flying apart at ever faster speeds, by observing distant, ancient exploding stars. This observation - named as Science magazine's "Breakthrough of the Year for 1998" - implies the existence of a mysterious, self-repelling property of space first proposed by Albert Einstein, which he called the cosmological constant. Researchers in England, France, Germany, and Sweden are among the members of the Supernova Cosmology Project based at Berkeley National Laboratory (headed by Saul Perlmutter) and the High-z Supernova Search Team based in Australia (led by Brian Schmidt)*TIS
BIRTHS
1864 Vladimir Andreevich Steklov (9 January 1864 – 30 May 1926) was a Soviet/Russian mathematician, mechanician and physicist. Steklov's primary scientific contribution is in the area of orthogonal functional sets. He introduced a class of closed orthogonal sets, developed asymptotic Liouville–Steklov method for orthogonal polynomials, proved theorems on generalized Fourier series, and developed an approximation technique later named Steklov function. He also worked on hydrodynamics and the theory of elasticity. Steklov also wrote a number of works on the history of science. Wik
1869 Richard Wilhelm Heinrich Abegg (9 Jan 1869; 3 Apr 1910) German physical chemist who, with Boländer proposed a theory of valency (1899) to explain the capacity of an atom to combine with another atom in light of the newly discovered presence of electrons within the atom. He saw that the configurations of electrons in the noble gas elements are particularly stable. Thus, a halide element, such as chlorine, with one electron less than a noble gas element, would easily tend to accept one electron. An alkali metal element, such as sodium, having one electron more than a noble gas element, would tend to give it up. Thus a sodium atom could transfer an electron to a chlorine atom, forming a positively charged sodium ion bound electrostatically to a negatively charged chloride ion. He died in a balloon crash. *TIS
1873 Birthdate of Hans Blichfeldt (9 Jan 1873 in Illar, Denmark - 16 Nov 1945 in Palo Alto, California, USA). When he graduated from Stanford in 1896 he didn’t have enough money to go to Europe for a doctorate, as was then the custom, so he borrowed the money from a Stanford professor (Rufus L Green). In one year he received his doctorate, summa cum laude, from Leipzig. *VFR
His lifework was devoted to group theory and number theory. Some of the many topics that he covered were diophantine approximations, orders of linear homogeneous groups, theory of geometry of numbers, approximate solutions of the integers of a set of linear equations, low-velocity fire angle, finite collineation groups, and characteristic roots.*SAU
1915 Mollie Orshansky, (January 9, 1915 – December 18, 2006), was an American economist and statistician who, in 1963–65, developed the Orshansky Poverty Thresholds, which are used in the United States as a measure of the income that a household must not exceed to be counted as poor.*Wik
1930 Jacob Theodore "Jack" Schwartz (January 9, 1930 – March 2, 2009) was an American mathematician, computer scientist, and professor of computer science at the New York University Courant Institute of Mathematical Sciences. He was the designer of the SETL programming language and the NYU Ultracomputer. He founded the New York University Department of Computer Science, chairing it from 1964 to 1980.
His research interests included: the theory of linear operators, von Neumann algebras, quantum field theory, time-sharing, parallel computing, programming language design and implementation, robotics, set-theoretic approaches in computational logic, proof and program verification systems; multimedia authoring tools; experimental studies of visual perception; multimedia and other high-level software techniques for analysis and visualization of bioinformatic data.
He authored 18 books and more than 100 papers and technical reports.*Wik
1950 Sir Alec Jefferys (9 Jan 1950, ) English geneticist who discovered the technique of DNA fingerprinting, used for unique identification of humans, animals and other organisms from their DNA material on 10 Sep 1984. This came about unexpectedly while Jeffreys was working on another project concerning genes for another purpose - to trace genetic markers through families to understand inheritance patterns of illness. DNA fingerprinting has become important for forensic science investigations, paternity issues, and detection of hereditary disease. He was knighted in 1994 for his research in genetics. *TIS
DEATHS
1586 Paul Wittich died. (c.1546 – 9 January 1586) In 1580, with the help of Tycho Brahe, he rediscovered the method of prostaphaeresis. *VFR German mathematician and astronomer whose Capellan geoheliocentric model, in which the inner planets Mercury and Venus orbit the sun but the outer planets Mars, Jupiter and Saturn orbit the Earth, may have directly inspired Tycho Brahe's more radically heliocentric geoheliocentric model in which all the 5 known primary planets orbited the Sun, which in turn orbited the stationary Earth.*Wik
Others think Wittich did not have, or need Brahe's help.
(I will leave it to Thony to someday explain to me why he credits Werner with the original discovery, rather than Christopher Clavius.... for students, Prosthaphaeresis is a combination of the Greek words for addition, prosth and subtraction aphaeresis. Prior to the discovery of logarithms it was very difficult to solve spherical triangle equations because it required several multiplications of sines and/or cosines to solve for a single unknown. Since in many tables sines and cosines were represented as chords of a radius of 10^7, it involved the equivalent of multiplying two seven digit numbers together by hand for each multiplication. In 1582, a Jesuit Priest named Christopher Clavius (or perhaps Johannes Werner) found a better way. He showed how to employ the trigonometric identity, Cos(A) Cos(B) = [Cos(a + b) + Cos(a - b)]/2 to make faster work of such problems.)
Wittich matriculated at Frankfurt an der Oder in 1576 and there he met John Craig, from Edinburgh, who was dean at Frankfurt an der Oder for several years before returning to Edinburgh. Let us remark that Craig then became personal physician to James VI of Scotland (later James I after the union of the crowns of England and Scotland). The connection with Craig is interesting, particularly in the light of a comment by the historian Anthony à Wood (1632-1695) that Napier got the idea for logarithms from a method brought back from the Continent by John Craig. It is certainly possible that the method referred to by Wood is one invented by Wittich since we know that Wittich found how to replace multiplication and division with addition and subtraction using the rules for sines and cosines of the sums and differences of angles. In one of his copies of De revolutionibus, Wittich used the blank space at the end of a chapter to write out an example of his method, known as prosthaphaeresis
1757 Bernard Le Bovier, sieur de Fontenelle (11 Feb 1657, 9 Jan 1757) French scientist and author, whose Conversations on the Plurality of Worlds (1686), was one of the first works to present science for the lay reader. He popularized the astronomical theories of Descartes. Many of the characteristic ideas of the Enlightenment are found in embryonic form in his works. From 1697 he became permanent secretary to the Académie des Sciences. He held the office for 42 years, and in this official capacity, he wrote the Histoire du renouvellement del Académie des Sciences (Paris, 3 vols., 1708, 1717, 1722) containing extracts and analyses of the proceedings, written with great simplicity and delicacy. Fontenelle presented many obituary notices to the Académie, including those of Newton and Leibniz. *TIS
1799 Maria Gaetana Agnesi (16 May 1718, 9 Jan 1799) Italian mathematician and philosopher who was the first woman in the Western world considered to be a mathematician. In Propositiones Philosophicae (1738) she presented a series of essays on philosophy and natural science that she had defended in discourses with invited intellectuals who were invited her father's home. In 1748, her two volumes of Analytical Institutions, were acclaimed by the academic world as one of the first and complete publications that brought together the works of various mathematicians on finite and infinitesimal analysis. After the death of her father in 1752, Agnesi entirely devoted herself and spent her money to do charitable work. She died in total poverty in the poorhouse of which she had been the director. *TIS Thony Christie tweets to ask, "Hypatia was not considered to be a mathematician?" To which I have no reply. Perhaps we should add ("modern") as part of the descriptor.
1848 Caroline Lucretia Herschel (16 Mar 1750, 9 Jan 1848) German-born British astronomer, sister of Sir William Herschel, who assisted in his astronomical researches making calculations associated with his studies. In her own telescope observations, she found three nebulae (1783) and eight comets (1786-97). In 1787, King George III gave Caroline a salary of 50 pounds per year as assistant to William. She published the Index to Flamsteed's Observations of the Fixed Stars and a list of his mistakes in 1797. At the age of 10 she had been struck with typhus, which subsequently stunted her growth. She never grew taller than 4' 3" and remained frail throughout her life. *TIS
[The following inscription is engraved on Miss Herschel's tomb. It begins: "Hier ruhet die irdische Hülle von CAROLINA HERSCHEL, Geboren zu Hannover den 16ten Marz 1750, Gestorben, den 9ten Januar 1848." But, for the convenience of our young readers, we give it in English:—
from The Project Gutenberg EBook of The Story of the Herschels, by Anonymous
1942 Heber Doust Curtis (27 Jun 1872, 9 Jan 1942) An American astronomer who is famed for debating Harlow Shapley on 26 Apr 1920 before the National academy of Sciences. He spoke for “island universes”—whereby spiral nebulae were composed of stars, and represented galaxies far outside the Milky Way. Shapley disagreed, believing that our galaxy was 300,000 light-years in diameter and included the spiral nebulae. By the end of 1924, Curtis was shown to be correct, when a paper from Edwin Hubble was read to the American Astronomical Society on 1 Jan 1925. Curtis had joined Lick Observatory after completing his Ph.D. in 1902. After his early work measuring radial velocities of the brighter stars, but in 1910 he became active in nebular photography, trying to find evidence of their nature as isolated independent star systems. *TIS
1973 Harry Schultz Vandiver (21 Oct 1882 in Philadelphia, Pennsylvania, USA - 9 Jan 1973 in Austin, Texas, USA) Harry developed an antagonism towards public education and left Central High School at an early age to work as a customshouse broker for his father's firm. D H Lehmer writes, "He was self-taught in his youth and must have had little patience with secondary education since he never graduated from high school. This impatience, especially with mathematical education, was to last the rest of his life."
When he was eighteen years old he began to solve many of the number theory problems which were posed in the American Mathematical Monthly, regularly submitting solutions. In addition to solving problems, he began to pose problems himself. By 1902 he was contributing papers to the Monthly. For example he published two short papers in 1902 A Problem Connected with Mersenne's Numbers and Applications of a Theorem Regarding Circulants.
In 1904 he collaborated with Birkhoff on a paper on the prime factors of a^n - b^n published in the Annals of Mathematics. In fact the result they proved was not new, although they were not aware of the earlier work which had been published by A S Bang in 1886. Also in the year 1904, Vandiver published On Some Special Arithmetic Congruences in the American Mathematical Monthly and, although still working as an agent for his father's firm, he did attend some graduate lectures at the University of Pennsylvania. He also began reading papers on algebraic number theory and embarked on a study of the work of Kummer, in particular his contributions to solving Fermat's Last Theorem. Over the next few years he published papers such as Theory of finite algebras (1912), Note on Fermat's last theorem (1914), and Symmetric functions formed by systems of elements of a finite algebra and their connection with Fermat's quotient and Bernoulli's numbers (1917).
The outbreak of World War I in 1914 did not directly affect the United States since the Democratic president Woodrow Wilson made a declaration of neutrality. This policy was controversial but popular enough to see him re-elected in 1916. However US shipping was being disrupted (and sunk) by German submarines and, under pressure from Republicans, Wilson declared war on Germany on 6 April 1917. Vandiver joined the United States Naval Reserve and continued to serve until 1919 when the war had ended. After leaving the Naval Reserve, Birkhoff persuaded Vandiver to become a professional mathematician and to accept a post at Cornell University in 1919. Despite having no formal qualifications, his excellent publication record clearly showed his high quality and he was appointed as an instructor. He also worked during the summer with Dickson at Chicago on his classic treatise History of the Theory of Numbers. In 1924 he moved to the University of Texas where he was appointed as an Associate Professor. He spent the rest of his career at the University of Texas, being promoted to full professor in 1925, then named as distinguished professor of applied mathematics and astronomy in 1947. He continued in this role until he retired in 1966 at the age of 84. *SAU
1975 Petr Sergeevich Novikov, (Aug. 15 (28), 1901, )Novikov’s main works deal with set theory, mathematical logic, the theory of algorithms, and group theory. He devised a powerful method called the index comparison principle for investigating problems of descriptive set theory. He proved that in the second class of projective sets there hold laws of separability inverse to those in the first projective class. He also developed a method, based on the concept of regular formula, of proving the consistency of formal systems. Novikov demonstrated the unsolvability of the problems of identity, conjugacy, and isomorphism in group theory. With his student S. I. Adian, he obtained a solution of Burnside’s problem of periodic groups. Founder of the school of mathematical logic in the USSR, Novikov received the Lenin Prize in 1957 and has been awarded two Orders of Lenin, the Order of the Red Banner of Labor, and various medals. *The Free Encyclopedia
1976 Rupert Wildt (25 Jun 1905, 9 Jan 1976) German-American astronomer who studied atmospheres of planets. He identified (1932) certain absorption bands (observed by Slipher) in the spectra of Jupiter and the outer planets as indicative of ammonia and methane as minor components of these planets which are primarily composed of hydrogen and helium. He speculated (1937) that droplets of formaldehyde formed the clouds of Venus, since water was not detected. (In fact, surface water is absent on Venus, but the clouds do contain water with sulphur and sulphuric acid.) In 1939, he realized the importance of the negative hydrogen ion for stellar opacity. By the 1940s, he proposed the greenhouse theory to explain how atmospheric gases produced unexpectedly high temperatures of Venus.*TIS
1979 Pier Luigi Nervi (21 Jun 1891, 9 Jan 1979) Italian engineer and architect who gained international recognition for his dramatic designs for large-span structures made possible with the use of reinforced concrete. In the 1940s he developed ideas for a reinforced concrete which allowed him to create structures of "strength, simplicity and grace". His services as an engineering consultant were highly sought as a result of his experimentation with structural concrete. His important works include a prefabricated 309-foot-span arch for the Turin Exhibition Building consisting of a single undulating large-span roof, the UNESCO building in Paris, the cathedral at New Norcia, near Perth, Australia, and as structural engineer for the first skyscraper in Italy, the Pirelli Building in Milan. *TIS
1989 Marshall Harvey Stone (8 April 1903 in New York, USA - 9 Jan 1989 in Madras, India) Stone is best known for the Stone-Weierstrass theorem on uniform approximation of continuous functions by polynomials.*SAU
1992 Hans Jenny (7 Feb 1899, 9 Jan 1992) Swiss agricultural chemist and pedologist (soil scientist) who developed numerical functions to describe soil in terms of five interacting factors in his classic book Factors of Soil Formation (1941). These related Climate (temperature and moisture); Organisms (those living on the soil and in the soil, vegetation and animals, fungi algae and bacteria, decay of organic matter, humus); Relief (topography, and geomorphic landscape); Parent Material (bedrock or sediment type); and Time (ranging from 100's to 1000's of years while maturity or equilibrium of soil development is attained). He moved to the U.S. in 1926. After retirement, he studied the soil relationships in the unusual ecological community of the Pygmy Forest in California, known for its stunted and twisted confers. *TIS
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
In 1816, Sir Humphry Davy's safety lamp was first used in a coal mine. Deadly explosions had been a continual hazard caused by the flammable gas, methane, leaking out of the coal seams ignited by the flame of a miner's lamp. There had been previous attempts by others to make a safety lantern. Davy applied a scientific approach to determine the suitable fineness of wire gauze placed around the flame which would avoid ignition of flammable gas outside. He determined that the holes in the gauze should be less than 1/22 inch in diameter, and that the wire itself should be between 1/40 to 1/60 inch thick. Since the flame changed colour in the presence of methane, it also served as a warning to the miner to take protective action.*TIS
1839 Henderson announces first stellar parallax. *VFR The Scottish Astronomer Royal, Thomas Henderson, published the results of his measurement, the first made of a stellar parallax. He observed the star Alpha Centauri from the Cape of Good Hope, South America. (It is not visible from Britain.) His measurements were made in 1831-33. After that time, but before Henderson completed his calculations and published his results, both Friedrich Bessel and Friedrich Struve had been recognized as the first to make measurements of stellar parallax.*TIS

In 1901, the first application for a patent for Meccano was submitted, as "Improvements in toy or educational devices for children and young people. Known at first as "Mechanics Made Easy," this invention of Frank Hornby became a worldwide success. The British patent (No. 587) showed the familiar perforated strips, pulleys, axles, brackets and clips assembled as a model railway crane with tracks that had operating points. The patent was published on 30 Nov 1901.*TIS (In the U S these are called "Erector Sets")
1947 According to Claude Shannon, it was on this day that John Tukey sent a Bell Labs memo creating the term bit, as an acronym for "Binary Information Digit." *Wik
1956 The Soviet Union issued a stamp commemorating the tenth anniversary of the death of Alexei N. Krylov (1863–1945), mathematician and naval architect. [Scott #1792] *VFR
1972 Mariner 9 transmitted black and white pictures of Mars back to Earth using the first order (32, 6, 16) Reed-Muller code. See Chester J. Salwach, “Codes that detect and correct errors,” The College Mathematics Journal, 19(1988), 402–416. *VFR
A mosaic of Mariner 9 frames, taken during the spacecraft's first orbit of Mars, showed the south polar cap dimly through a great dust storm.
 |
| *aip.org |
1991 After the Fullerenes discovery and Nobel Prize the session of the House of Lords entertained a question from Lord Errol of Hale as to "What steps the government was taking to encourage the use of Fullerines in science and industry?" The question prompted questions on what was a Fullerene, what shape did it have and finally, this brilliant exchange:
Lord Campbell of Alloway: "My Lords, what does it do?"
Lord Reay: "My Lords, it is thought that it may have several possible uses... All that is speculation. It may turn out to have no uses at all."
Earl Russell: "My Lords, can one say that it does nothing in particular, and does it very well." *Siobhan Roberts, King of Infinite Space
In 1998, two teams of international collaborations of scientists announced the discovery that galaxies are accelerating, flying apart at ever faster speeds, by observing distant, ancient exploding stars. This observation - named as Science magazine's "Breakthrough of the Year for 1998" - implies the existence of a mysterious, self-repelling property of space first proposed by Albert Einstein, which he called the cosmological constant. Researchers in England, France, Germany, and Sweden are among the members of the Supernova Cosmology Project based at Berkeley National Laboratory (headed by Saul Perlmutter) and the High-z Supernova Search Team based in Australia (led by Brian Schmidt)*TIS
1864 Vladimir Andreevich Steklov (9 January 1864 – 30 May 1926) was a Soviet/Russian mathematician, mechanician and physicist. Steklov's primary scientific contribution is in the area of orthogonal functional sets. He introduced a class of closed orthogonal sets, developed asymptotic Liouville–Steklov method for orthogonal polynomials, proved theorems on generalized Fourier series, and developed an approximation technique later named Steklov function. He also worked on hydrodynamics and the theory of elasticity. Steklov also wrote a number of works on the history of science. Wik
1869 Richard Wilhelm Heinrich Abegg (9 Jan 1869; 3 Apr 1910) German physical chemist who, with Boländer proposed a theory of valency (1899) to explain the capacity of an atom to combine with another atom in light of the newly discovered presence of electrons within the atom. He saw that the configurations of electrons in the noble gas elements are particularly stable. Thus, a halide element, such as chlorine, with one electron less than a noble gas element, would easily tend to accept one electron. An alkali metal element, such as sodium, having one electron more than a noble gas element, would tend to give it up. Thus a sodium atom could transfer an electron to a chlorine atom, forming a positively charged sodium ion bound electrostatically to a negatively charged chloride ion. He died in a balloon crash. *TIS
1873 Birthdate of Hans Blichfeldt (9 Jan 1873 in Illar, Denmark - 16 Nov 1945 in Palo Alto, California, USA). When he graduated from Stanford in 1896 he didn’t have enough money to go to Europe for a doctorate, as was then the custom, so he borrowed the money from a Stanford professor (Rufus L Green). In one year he received his doctorate, summa cum laude, from Leipzig. *VFR
His lifework was devoted to group theory and number theory. Some of the many topics that he covered were diophantine approximations, orders of linear homogeneous groups, theory of geometry of numbers, approximate solutions of the integers of a set of linear equations, low-velocity fire angle, finite collineation groups, and characteristic roots.*SAU
1915 Mollie Orshansky, (January 9, 1915 – December 18, 2006), was an American economist and statistician who, in 1963–65, developed the Orshansky Poverty Thresholds, which are used in the United States as a measure of the income that a household must not exceed to be counted as poor.*Wik
1930 Jacob Theodore "Jack" Schwartz (January 9, 1930 – March 2, 2009) was an American mathematician, computer scientist, and professor of computer science at the New York University Courant Institute of Mathematical Sciences. He was the designer of the SETL programming language and the NYU Ultracomputer. He founded the New York University Department of Computer Science, chairing it from 1964 to 1980.
His research interests included: the theory of linear operators, von Neumann algebras, quantum field theory, time-sharing, parallel computing, programming language design and implementation, robotics, set-theoretic approaches in computational logic, proof and program verification systems; multimedia authoring tools; experimental studies of visual perception; multimedia and other high-level software techniques for analysis and visualization of bioinformatic data.
He authored 18 books and more than 100 papers and technical reports.*Wik
1950 Sir Alec Jefferys (9 Jan 1950, ) English geneticist who discovered the technique of DNA fingerprinting, used for unique identification of humans, animals and other organisms from their DNA material on 10 Sep 1984. This came about unexpectedly while Jeffreys was working on another project concerning genes for another purpose - to trace genetic markers through families to understand inheritance patterns of illness. DNA fingerprinting has become important for forensic science investigations, paternity issues, and detection of hereditary disease. He was knighted in 1994 for his research in genetics. *TIS
1586 Paul Wittich died. (c.1546 – 9 January 1586) In 1580, with the help of Tycho Brahe, he rediscovered the method of prostaphaeresis. *VFR German mathematician and astronomer whose Capellan geoheliocentric model, in which the inner planets Mercury and Venus orbit the sun but the outer planets Mars, Jupiter and Saturn orbit the Earth, may have directly inspired Tycho Brahe's more radically heliocentric geoheliocentric model in which all the 5 known primary planets orbited the Sun, which in turn orbited the stationary Earth.*Wik
Others think Wittich did not have, or need Brahe's help.
It is considered unlikely that Tycho was actually involved in the re-invention/re-discovery of prosthaphaeresis although he himself claimed that he was. The first person to publish an account of prosthaphaeresis was Nicolaus Reimers Baer who attributed his knowledge of it to Jost Bürgi who he said had learnt it from Paul Wittich. It was at this point that Tycho claimed that he had discovered the technique together with Wittich, as part of his dispute with Baer on the origins of the so-called Tychonic astronomical system. Tycho accused Baer of having stolen the system. However Tycho’s claim is highly dubious, although Bürgi and Baer both obviously fully understood the prosthaphaerasis method and could utilise it perfectly, Tycho just as obviously didn’t understand it properly and made serious errors when using it. Not the achievements of somebody who supposedly invented the method. Given these facts it is now accepted that Wittich either re-invented the method or had access to a manuscript containing Johannes Werner’s original discovery and taught the method to both Bürgi who understood it and Tycho who didn’t really.*Thony Christie
(I will leave it to Thony to someday explain to me why he credits Werner with the original discovery, rather than Christopher Clavius.... for students, Prosthaphaeresis is a combination of the Greek words for addition, prosth and subtraction aphaeresis. Prior to the discovery of logarithms it was very difficult to solve spherical triangle equations because it required several multiplications of sines and/or cosines to solve for a single unknown. Since in many tables sines and cosines were represented as chords of a radius of 10^7, it involved the equivalent of multiplying two seven digit numbers together by hand for each multiplication. In 1582, a Jesuit Priest named Christopher Clavius (or perhaps Johannes Werner) found a better way. He showed how to employ the trigonometric identity, Cos(A) Cos(B) = [Cos(a + b) + Cos(a - b)]/2 to make faster work of such problems.)
Wittich matriculated at Frankfurt an der Oder in 1576 and there he met John Craig, from Edinburgh, who was dean at Frankfurt an der Oder for several years before returning to Edinburgh. Let us remark that Craig then became personal physician to James VI of Scotland (later James I after the union of the crowns of England and Scotland). The connection with Craig is interesting, particularly in the light of a comment by the historian Anthony à Wood (1632-1695) that Napier got the idea for logarithms from a method brought back from the Continent by John Craig. It is certainly possible that the method referred to by Wood is one invented by Wittich since we know that Wittich found how to replace multiplication and division with addition and subtraction using the rules for sines and cosines of the sums and differences of angles. In one of his copies of De revolutionibus, Wittich used the blank space at the end of a chapter to write out an example of his method, known as prosthaphaeresis
And this was precisely one of the pages that John Craig had transcribed into his copy of 'De revolutionibus' when he was being tutored by Wittich in Frankfurt an der Oder in 1576. In turn he took his annotated copy with him when he returned to Edinburgh, and he surely must have shown it to Napier who was living in a castle in the area.
1757 Bernard Le Bovier, sieur de Fontenelle (11 Feb 1657, 9 Jan 1757) French scientist and author, whose Conversations on the Plurality of Worlds (1686), was one of the first works to present science for the lay reader. He popularized the astronomical theories of Descartes. Many of the characteristic ideas of the Enlightenment are found in embryonic form in his works. From 1697 he became permanent secretary to the Académie des Sciences. He held the office for 42 years, and in this official capacity, he wrote the Histoire du renouvellement del Académie des Sciences (Paris, 3 vols., 1708, 1717, 1722) containing extracts and analyses of the proceedings, written with great simplicity and delicacy. Fontenelle presented many obituary notices to the Académie, including those of Newton and Leibniz. *TIS
1799 Maria Gaetana Agnesi (16 May 1718, 9 Jan 1799) Italian mathematician and philosopher who was the first woman in the Western world considered to be a mathematician. In Propositiones Philosophicae (1738) she presented a series of essays on philosophy and natural science that she had defended in discourses with invited intellectuals who were invited her father's home. In 1748, her two volumes of Analytical Institutions, were acclaimed by the academic world as one of the first and complete publications that brought together the works of various mathematicians on finite and infinitesimal analysis. After the death of her father in 1752, Agnesi entirely devoted herself and spent her money to do charitable work. She died in total poverty in the poorhouse of which she had been the director. *TIS Thony Christie tweets to ask, "Hypatia was not considered to be a mathematician?" To which I have no reply. Perhaps we should add ("modern") as part of the descriptor.
1848 Caroline Lucretia Herschel (16 Mar 1750, 9 Jan 1848) German-born British astronomer, sister of Sir William Herschel, who assisted in his astronomical researches making calculations associated with his studies. In her own telescope observations, she found three nebulae (1783) and eight comets (1786-97). In 1787, King George III gave Caroline a salary of 50 pounds per year as assistant to William. She published the Index to Flamsteed's Observations of the Fixed Stars and a list of his mistakes in 1797. At the age of 10 she had been struck with typhus, which subsequently stunted her growth. She never grew taller than 4' 3" and remained frail throughout her life. *TIS
[The following inscription is engraved on Miss Herschel's tomb. It begins: "Hier ruhet die irdische Hülle von CAROLINA HERSCHEL, Geboren zu Hannover den 16ten Marz 1750, Gestorben, den 9ten Januar 1848." But, for the convenience of our young readers, we give it in English:—
HERE RESTS THE EARTHLY CASE OFThis epitaph was mainly written by Miss Herschel herself, and the allusion to her brother is characteristic.]
CAROLINE HERSCHEL.
BORN AT HANOVER, MARCH 10, 1750.
DIED JANUARY 9, 1848.
"The eyes of her now glorified were, while here below, directed towards the starry heavens. Her own discoveries of comets, and her share in the immortal labours of her brother, William Herschel, bear witness of this to succeeding ages.
"The Royal Irish Academy of Dublin, and the Royal Astronomical Society of London, enrolled her name among their members.
"At the age of 97 years 10 months, she fell asleep in calm rest, and in the full possession of her faculties; following into a better life her father, Isaac Herschel, who lived to the age of 60 years, 2 months, 17 days, and has lain buried not far off since the 29th of March 1767."
from The Project Gutenberg EBook of The Story of the Herschels, by Anonymous
1942 Heber Doust Curtis (27 Jun 1872, 9 Jan 1942) An American astronomer who is famed for debating Harlow Shapley on 26 Apr 1920 before the National academy of Sciences. He spoke for “island universes”—whereby spiral nebulae were composed of stars, and represented galaxies far outside the Milky Way. Shapley disagreed, believing that our galaxy was 300,000 light-years in diameter and included the spiral nebulae. By the end of 1924, Curtis was shown to be correct, when a paper from Edwin Hubble was read to the American Astronomical Society on 1 Jan 1925. Curtis had joined Lick Observatory after completing his Ph.D. in 1902. After his early work measuring radial velocities of the brighter stars, but in 1910 he became active in nebular photography, trying to find evidence of their nature as isolated independent star systems. *TIS
1973 Harry Schultz Vandiver (21 Oct 1882 in Philadelphia, Pennsylvania, USA - 9 Jan 1973 in Austin, Texas, USA) Harry developed an antagonism towards public education and left Central High School at an early age to work as a customshouse broker for his father's firm. D H Lehmer writes, "He was self-taught in his youth and must have had little patience with secondary education since he never graduated from high school. This impatience, especially with mathematical education, was to last the rest of his life."
When he was eighteen years old he began to solve many of the number theory problems which were posed in the American Mathematical Monthly, regularly submitting solutions. In addition to solving problems, he began to pose problems himself. By 1902 he was contributing papers to the Monthly. For example he published two short papers in 1902 A Problem Connected with Mersenne's Numbers and Applications of a Theorem Regarding Circulants.
In 1904 he collaborated with Birkhoff on a paper on the prime factors of a^n - b^n published in the Annals of Mathematics. In fact the result they proved was not new, although they were not aware of the earlier work which had been published by A S Bang in 1886. Also in the year 1904, Vandiver published On Some Special Arithmetic Congruences in the American Mathematical Monthly and, although still working as an agent for his father's firm, he did attend some graduate lectures at the University of Pennsylvania. He also began reading papers on algebraic number theory and embarked on a study of the work of Kummer, in particular his contributions to solving Fermat's Last Theorem. Over the next few years he published papers such as Theory of finite algebras (1912), Note on Fermat's last theorem (1914), and Symmetric functions formed by systems of elements of a finite algebra and their connection with Fermat's quotient and Bernoulli's numbers (1917).
The outbreak of World War I in 1914 did not directly affect the United States since the Democratic president Woodrow Wilson made a declaration of neutrality. This policy was controversial but popular enough to see him re-elected in 1916. However US shipping was being disrupted (and sunk) by German submarines and, under pressure from Republicans, Wilson declared war on Germany on 6 April 1917. Vandiver joined the United States Naval Reserve and continued to serve until 1919 when the war had ended. After leaving the Naval Reserve, Birkhoff persuaded Vandiver to become a professional mathematician and to accept a post at Cornell University in 1919. Despite having no formal qualifications, his excellent publication record clearly showed his high quality and he was appointed as an instructor. He also worked during the summer with Dickson at Chicago on his classic treatise History of the Theory of Numbers. In 1924 he moved to the University of Texas where he was appointed as an Associate Professor. He spent the rest of his career at the University of Texas, being promoted to full professor in 1925, then named as distinguished professor of applied mathematics and astronomy in 1947. He continued in this role until he retired in 1966 at the age of 84. *SAU
1975 Petr Sergeevich Novikov, (Aug. 15 (28), 1901, )Novikov’s main works deal with set theory, mathematical logic, the theory of algorithms, and group theory. He devised a powerful method called the index comparison principle for investigating problems of descriptive set theory. He proved that in the second class of projective sets there hold laws of separability inverse to those in the first projective class. He also developed a method, based on the concept of regular formula, of proving the consistency of formal systems. Novikov demonstrated the unsolvability of the problems of identity, conjugacy, and isomorphism in group theory. With his student S. I. Adian, he obtained a solution of Burnside’s problem of periodic groups. Founder of the school of mathematical logic in the USSR, Novikov received the Lenin Prize in 1957 and has been awarded two Orders of Lenin, the Order of the Red Banner of Labor, and various medals. *The Free Encyclopedia
1976 Rupert Wildt (25 Jun 1905, 9 Jan 1976) German-American astronomer who studied atmospheres of planets. He identified (1932) certain absorption bands (observed by Slipher) in the spectra of Jupiter and the outer planets as indicative of ammonia and methane as minor components of these planets which are primarily composed of hydrogen and helium. He speculated (1937) that droplets of formaldehyde formed the clouds of Venus, since water was not detected. (In fact, surface water is absent on Venus, but the clouds do contain water with sulphur and sulphuric acid.) In 1939, he realized the importance of the negative hydrogen ion for stellar opacity. By the 1940s, he proposed the greenhouse theory to explain how atmospheric gases produced unexpectedly high temperatures of Venus.*TIS
1979 Pier Luigi Nervi (21 Jun 1891, 9 Jan 1979) Italian engineer and architect who gained international recognition for his dramatic designs for large-span structures made possible with the use of reinforced concrete. In the 1940s he developed ideas for a reinforced concrete which allowed him to create structures of "strength, simplicity and grace". His services as an engineering consultant were highly sought as a result of his experimentation with structural concrete. His important works include a prefabricated 309-foot-span arch for the Turin Exhibition Building consisting of a single undulating large-span roof, the UNESCO building in Paris, the cathedral at New Norcia, near Perth, Australia, and as structural engineer for the first skyscraper in Italy, the Pirelli Building in Milan. *TIS
1989 Marshall Harvey Stone (8 April 1903 in New York, USA - 9 Jan 1989 in Madras, India) Stone is best known for the Stone-Weierstrass theorem on uniform approximation of continuous functions by polynomials.*SAU
1992 Hans Jenny (7 Feb 1899, 9 Jan 1992) Swiss agricultural chemist and pedologist (soil scientist) who developed numerical functions to describe soil in terms of five interacting factors in his classic book Factors of Soil Formation (1941). These related Climate (temperature and moisture); Organisms (those living on the soil and in the soil, vegetation and animals, fungi algae and bacteria, decay of organic matter, humus); Relief (topography, and geomorphic landscape); Parent Material (bedrock or sediment type); and Time (ranging from 100's to 1000's of years while maturity or equilibrium of soil development is attained). He moved to the U.S. in 1926. After retirement, he studied the soil relationships in the unusual ecological community of the Pygmy Forest in California, known for its stunted and twisted confers. *TIS
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell




No comments:
Post a Comment