He who understands Archimedes and Apollonius will admire less
the achievements of the foremost men of later times.
~Gottfried LeibnizThe 318th day of the year; According to Police chief Wiggum on The Simpsons; 318 is the Police code for waking a police officer in episode 5F06 Reality Bites.
If 22 is partitioned into distinct integer parts in all possible ways, there will be 318 total parts.
318 is a palindrome in base 9, 3839
1680 The Great Comet of 1680, Kirch's Comet, and Newton's Comet, has the distinction of being the first comet discovered by telescope. Discovered by Gottfried Kirch on 14 November 1680, New Style, it became one of the brightest comets of the 17th century--reputedly visible even in daytime--and was noted for its spectacularly long tail. Passing only 0.4 AUs from Earth on 30 November, it sped around an incredibly close perihelion of .006 AU (898,000 km) on 18 December 1680, reaching its peak brightness on 29 December as it rushed outward again. It was last observed on 19 March 1681. As of December 2010 the comet was about 252.1 A.U. from the Sun. While the Kirch Comet of 1680-1681 was discovered and subsequently named for Gottfried Kirch , credit must also be given to the Jesuit, Eusebio Kino, who charted the comet’s course. During his delayed departure for Mexico, Kino began his observations of the comet in Cadíz in late 1680. Upon his arrival in Mexico City, he published his Exposisión astronómica de el [sic] cometa (Mexico City, 1681) in which he presented his findings. Kino’s Exposisión astronómica is among one of the earliest scientific treatises published by a European in the New World. Aside from its brilliance, it is probably most noted for being used by Isaac Newton to test and verify Kepler's laws. *Wik
The orbit of the comet of 1680, fit to a parabola, as shown in Isaac Newton's Principia
1750 Euler creates the term “edge” for polyhedral. In a letter to Christian Goldbach, Euler writes, “the junctures where two faces come together along their sides, which, for lack of an accepter term, I call edges.” *Dave Richeson, Euler’s Gem, pg 63 "It astonishes me that these general properties of stereometry have not, as far as I know, been noticed by anyone else". *Carlo Beenakker at Math Overflow
1757 After incremental computations of the gravitational influences and motion of Jupiter and Saturn on the predicted return of Halley's comet, Alexis-Claude Clairaut presents the results to the Academies de Sciences. The computational work of the team of Clairaut, with La Lande and Nicole-Reine Lepaute, (having removed Saturn from the last few months calculations to speed the results) had predicted a window of arrival between March 15 and May 15 (1758). The unruly comet reached perihelion on the 13th of March.
This was one of the first "division of Labor" efforts to use human calculators to work on a joint project, Their error was almost exclusively the result of the effect of Uranus and Neptune, planets unknown at that time.
*David A Grier, When Computers Were Human
1922 The British Broadcasting Company's first weather forecast was broadcast on radio on November 14, 1922 in London. The forecast was prepared by the Met Office. From March 26, 1923, these weather forecasts became a daily service.
1949 France issued stamps honoring Voltaire and the Comte de Buffon (1707-1778). [Scott #B239, B241]. *VFR
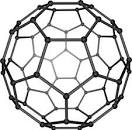
1985 The discovery of the first fullerenes is announced in the 14 Nov 1985, issue of the journal Nature. Robert F. Curl, Jr. American chemist who with Richard E. Smalley and Sir Harold W. Kroto discovered the first fullerene, a spherical cluster of carbon atoms, in 1985. The discovery opened a new branch of chemistry, and all three men were awarded the 1996 Nobel Prize for Chemistry for their work. In Sep 1985 Curl met with Kroto of the University of Sussex, Eng., and Smalley, a colleague at Rice, and, in 11 days of research, they discovered fullerenes. *TIS
The C_60 Fullerine
1845 Ulisse Dini (14 November 1845 – 28 October 1918) was an Italian mathematician and politician born in Pisa. One of his professors was Enrico Betti. In 1865, a scholarship enabled him to visit Paris, where he studied under Charles Hermite as well as Joseph Bertrand, and published several papers. In 1866, he was appointed to the University of Pisa, where he taught algebra and geodesy. In 1871, he succeeded Betti as professor for analysis and geometry. From 1888 until 1890, Dini was rettore (chief executive) of the Pisa university, and of the Scuola Normale Superiore from 1908 until his death in 1918. He was also active as a politician: in 1871 he was voted into the Pisa city council, and in 1880, he became a member of the Italian parliament.
Dini worked in the field of analysis during a time when it was begun to be based on rigorous foundations. He proved a criterion for the convergence of Fourier series and investigated the potential theory and differential geometry of surfaces, based on work by Eugenio Beltrami.
The implicit function theorem is known in Italy as the Dini's theorem.*Wik
1882 Robert Lee Moore (14 November 1882 – 4 October 1974) was an American mathematician, known for his work in general topology and the Moore method of teaching university mathematics. Moore entered the University of Texas at the unusually low age of 16, in 1898, already knowing calculus thanks to self-study. He completed the B.Sc. in three years instead of the usual four; his teachers included G. B. Halsted and L. E. Dickson. After a year as a teaching fellow at Texas, he taught high school for a year in Marshall, Texas.
An assignment of Halsted's led Moore to prove that one of Hilbert's axioms for geometry was redundant. When E. H. Moore (no relation), who headed the Department of Mathematics at the University of Chicago, and whose research interests were on the foundations of geometry, heard of Robert's feat, he arranged for a scholarship that would allow Robert to study for a doctorate at Chicago. Oswald Veblen supervised Moore's 1905 thesis, titled Sets of Metrical Hypotheses for Geometry.
Moore then taught one year at the University of Tennessee, two years at Princeton University, and three years at Northwestern University. In 1910, he married Margaret MacLelland Key of Brenham, Texas; they had no children. In 1911, he took up a position at the University of Pennsylvania.
In 1920, Moore happily returned to the University of Texas at Austin as an associate professor, and was promoted to full professor three years later. In 1951, he went on half pay, but continued to teach his habitual five classes a year, including a section of freshman calculus, until the University authorities forced his definitive retirement in 1969, his 87th year. In 1973, the University of Texas honored him by giving the name Moore Hall to a new building housing the physics, mathematics, and astronomy departments.*Wik
In 2016, students demanded the building be renamed because of Moore's racist treatment of African American students.
 |
| *Wik |
Paulette Libermann (November 14 1919 in Paris ,July 10 2007 in Montrouge ) was a French mathematician , her primary work was in differential geometry and symplectic geometry employed. *Wik
1943 Peter Norton (November 14, 1943 - )was born in Aberdeen, Washington. Norton would first come to note for producing tools that could retrieve erased data from DOS disks that would eventually be compiled into suite called Norton Utilities. Norton founded Peter Norton Computing, which produced both software utilities as well as publishing several manuals and books. In 1990, Norton sold his company to Symantec, which would keep the Norton name alive for more than a decade following the purchase. He currently heads up The Peter Norton Family Foundation, which is a major philanthropic group supporting the arts and human social services. *CHM
1716 Gottfried Wilhelm Leibniz (1 Jul 1646, 14 Nov 1716) spent his closing years enfeebled by disease, harassed by controversy, embittered by neglect; but to the last he preserved the indomitable energy and power of work to which is largely due the position he holds as, more perhaps than any one in modern times, a man of almost universal attainments and almost universal genius. At Hanover, Eckhart, his secretary, was his only mourner; "he was buried", says an eyewitness, "more like a robber than what he really was, the ornament of his country."*Georgi Dalakov, History of Computers web-site ---
German philosopher, mathematician, and political adviser, important both as a metaphysician and as a logician and distinguished also for his independent invention of the differential and integral calculus. Through meeting with such scholars as Christian Huygens in Paris and with members of the Royal Society, including Robert Boyle, during two trips to London in 1673 and 1676, Leibniz was introduced to the outstanding problems challenging the mathematicians and physicists of Europe. Leibniz's independently discovered differential and integral calculus (published 1684), but became involved in a bitter priority dispute with Isaac Newton, whose ideas on the calculus were developed earlier (1665), but published later (1687). *TIS
1798 Naonobu Ajima (1732 – May 20, 1798) was a Japanese mathematician and astronomer who developed a theory of integration. Ajima's work leaned towards geometry despite the strong algebraic numerical tradition in the Seki school. He developed methods of integration, developing the 'yenri' method which had been devised earlier and was used to find the area of a circle using inscribed polygons in a similar manner to the methods of Archimedes. Ajima refined the method subdividing the chord of an arc into equal small segments, so producing a method similar to that of the definite integral. He presented this in Kohai jutsu kai, giving a method which is the high point that traditional Japanese mathematics reached in methods of integration Immediately after developing this method of integration, Ajima developed a method for computing volumes by double integration. The method was developed to solve the problem of finding the volume of the intersection of two cylinders and he presented it in Enchu kokuen jutsu.
Ajima also solved the Malfatti problem. It is today called the Malfatti Problem since it was posed in 1803 by Gian Francesco Malfatti, but Ajima's contributions were made around 30 years earlier. The problem is, given an arbitrary triangle, find how to place three non-overlapping circles so that the area of that part of the triangle not covered by a circle is a minimum. Malfatti assumed that the solution would involve three circles, each of which is tangent to the other two. It is precisely the problem of maximizing the area of the three mutually tangent circles that Ajima solved in Fukyu sampo. However, Malfatti's assumption is wrong and it was shown in 1992 that to maximize the area of the three non-overlapping circles, they are never mutually tangent. This, of course, is not relevant to Ajima's problem which is only posed in terms of maximizing the area of three non-overlapping mutually tangent circles.
After Ajima's death, he was buried in the Jorin-jo Temple, Mita, Tokyo, and his grave can still be visited today. *SAU
1886 Alexandre-Emile Beguyer de Chancourtois (20 Jan 1820; 14 Nov 1886) French geologist who was the first to arrange the chemical elements in order of atomic weights (1862). De Chancourtois plotted the atomic weights on the surface of a cylinder with a circumference of 16 units, the approximate atomic weight of oxygen. The resulting helical curve which he called the telluric helix brought closely related elements onto corresponding points above or below one another on the cylinder. Thus, he suggested that "the properties of the elements are the properties of numbers." Although his publication was significant, it was ignored by chemists as it was written in the language of geology, and the editors omitted a crucial explanatory table. It was Dmitry Mendeleyev's table published in 1869 that became most recognized.*TIS
1919 John Aitken (18 Sep 1839, 14 Nov 1919) Scottish physicist and meteorologist known for his research work on atmospheric dust, the formation of dew, cyclones and evaporation. He invented the koniscope to detect and study atmospheric dust particles. He determined that condensation of atmospheric water vapor from clouds and fogs begins on the surface of microscopic particles (now known as Aitken nuclei) as a crucial step in the formation of rain and dew. Combustion produces a profusion of such particles. Suffering from ill health, he worked from a laboratory in his Falkirk home. Much of his work was published in the journals of the Royal Society of Edinburgh. *TIS
1934 Alice Liddlell Hargraves ( 4 May 1852 – 16 November 1934) died, age 82. She was the Alice of Lewis Carroll's classic, Alice’s Adventures Underground. *VFR
For most of her life, she lived in and around Lyndhurst in the New Forest. After her death she was cremated and her ashes were buried in the graveyard of the church of St. Michael & All Angels, Lyndhurst *Wik
1954 Ernst Fischer (12 July 1875; Vienna, Austria – 14 November 1954) He worked alongside both Mertens and Minkowski at the Universities of Vienna and Zurich, respectively. He later became professor at the University of Erlangen, where he worked with Emmy Noether.
His main area of research was mathematical analysis, specifically orthonormal sequences of functions which laid groundwork for the emergence of the concept of a Hilbert space.
The Riesz–Fischer theorem in Lebesgue integration is named in his honour. *Wik
1971 Hanna Neumann (2 Feb 1914 in Lankwitz, Berlin, Germany - 14 Nov 1971 in Ottawa, Canada) worked in group theory. Her thesis examined free products with amalgamation. Later she worked on varieties of groups and her book Varieties of Groups (1967) is a classic.*SAU
2014 Eugene Borisovich Dynkin ( May 11, 1924 — 14 November 2014) was a Soviet and American mathematician. He has made contributions to the fields of probability and algebra, especially semisimple Lie groups, Lie algebras, and Markov processes. The Dynkin diagram, the Dynkin system, and Dynkin's lemma are named for him.
In 1968, Dynkin was forced to transfer from the Moscow University to the Central Economic Mathematical Institute of the USSR Academy of Sciences. He worked there on the theory of economic growth and economic equilibrium. He remained at the Institute until 1976, when he emigrated to the United States. In 1977, he became a professor at Cornell University, where he died in 2014. *Wik
1958 Kristie Irene Macrakis (March 11, 1958 – November 14, 2022) was an American historian of science, author and professor in the School of History, Technology and Society at the Georgia Institute of Technology. She was the author or editor of five books and was widely known for her work at the intersection of history of espionage and history of science and technology.
Macrakis received her PhD in the history of science at Harvard University. After teaching at Harvard University for a year as a lecturer, Macrakis spent a year in Berlin on an Alexander von Humboldt Foundation Chancellor's Scholar for Future Leaders, before taking up a position at Michigan State University where she advanced from Assistant to Full Professor, before taking up a Full Professor position at Georgia Tech.
Prisoners, Lovers, and Spies (2014) and Seduced by Secrets (2008) were her single authored books. Nigel Jones wrote in The Spectator that Prisoners, Lovers and Spies is "beguilingly informative and sweeping survey of hidden communication.]Kirkus Reviews named it one of the best nonfiction books of 2014 and called it "lively...engaging" and "An engrossing study of unseen writing and the picaresque misadventures of those who employ it."
Seduced by Secrets was hailed as the "best book" on the Ministry for State Security by Benjamin Fischer in the International Journal of Intelligence and CounterIntelligence,[while Joseph Goulden, of the Washington Times, gave it "a five cloak-and-dagger rating. Good reading for the specialist and the layman alike."
Macrakis was also the author of numerous articles, both scholarly and popular. While a graduate student at Harvard she found that the Rockefeller Foundation funded science in Nazi Germany; that work was covered in the Frankfurter Allgemeine Zeitung. (Frankfurter Allgemeine Zeitung, 29 October 1986). Her most widely read popular magazine article is "The Case of Agent Gorbachev," published in American Scientist.
Following a brief illness, Macrakis died on November 14, 2022, at the age of 64.
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell









No comments:
Post a Comment