~Paul Auster, The Music of Chance
The 138th day of the year; 138 is a sphenic number(the product of three primes from the Greek for "wedge shaped") and is the smallest product of 3 primes, such that in base 10, the third prime is a concatenation of the other two: (2)(3)(23)
138 is the sum of four consecutive primes (29 + 31 + 37 + 41),
138 is a palindrome in base 8 (212)
138 is a congruent number, it is the area of a right triangle with all sides rational.
138 is an Ulam Number, a member of the sequence created by a sieve process by Stan Ulam in 1964. It begins with the numbers 1, 2, and then each successive term is the smallest larger number that is the sum of two distinct numbers in the sequence, in a single way. The first few numbers are 1, 2, 3, 4, 6, 8, 11,,, Five is missing because its sum can be created in two different ways, 2+3 or 1+4.
See more math facts at Math Day of the Year Facts
1618 Kepler, On how he discovered his Third law:
...and if you want the exact moment in time, it was conceived mentally on 8th March in this year one thousand six hundred an eighteen, but submitted to calculation in an unlucky way, and therefore rejected as false, and finally returning on the 15th of May and adopting a new line of attack, stormed the darkness of my mind. So strong was the support from the combination of my labor of seventeen years on the observations of Brahe and the present study, which conspired together, that at first I believed I was dreaming, and assuming my conclusion among my basic premises. But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialterate proportion of their mean distances ...
* Harmonice mundi (Linz, 1619) Book 5, Chapter 3, trans. Aiton, Duncan and Field, p. 411.
", as Kepler later recalled, on the 8th of March in the year 1618, something marvelous "appeared in my head". He suddenly realized that
III. The proportion between the periodic times of any two planets is precisely one and a half times the proportion of the mean distances.
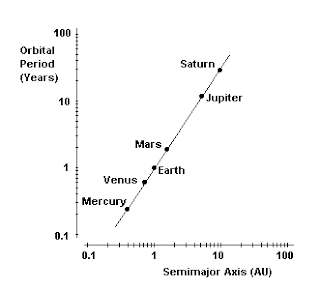
Presumably he used the word “proportion” here to signify the logarithm of the ratio, so he is asserting that log(T1/T2) = (3/2)log(r1/r2), where Tj are the periods and rj are the mean radii of the orbits of any two planets. In the form of a diagram, his insight looks like this:
At first it may seem surprising that it took a mathematically insightful man like Kepler over twelve years of intensive study to notice this simple linear relationship between the logarithms of the orbital periods and radii. In modern data analysis the log-log plot is a standard format for analyzing physical data. However, we should remember that logarithmic scales had not yet been invented in 1605. A more interesting question is why, after twelve years of struggle, this way of viewing the data suddenly "appeared in his head" early in 1618. (Kepler made some errors in the calculations in March, and decided the data didn't fit, but two months later, on May 15 the idea "came into his head" again, and this time he got the computations right, and thought he was dreaming because the fit is so exact.)
Is it just coincidental that John Napier's "Mirifici Logarithmorum Canonis Descripto" (published in 1614) was first seen by Kepler towards the end of the year 1616? We know that Kepler was immediately enthusiastic about logarithms, which is not surprising, considering the masses of computation involved in preparing the Rudolphine Tables. Indeed, he even wrote a book of his own on the subject in 1621. It's also interesting that Kepler initially described his "Third Law" in terms of a 1.5 ratio of proportions, exactly as it would appear in a log-log plot, rather than in the more familiar terms of squared periods and cubed distances. It seems as if a purely mathematical invention, namely logarithms, whose intent was simply to ease the burden of manual arithmetical computations, may have led directly to the discovery/formulation of an important physical law, i.e., Kepler's third law of planetary motion. (Ironically, Kepler's academic mentor, Michael Maestlin, chided him − perhaps in jest? − for even taking an interest in logarithms, remarking that "it is not seemly for a professor of mathematics to be childishly pleased about any shortening of the calculations".) By the 18th of May, 1618, Kepler had fully grasped the logarithmic pattern in the planetary orbits: 'Now, because 18 months ago the first dawn, three months ago the broad daylight, but a very few days ago the full Sun of a most highly remarkable spectacle has risen, nothing holds me back.' "
*mathpages.com
in paper to St. Petersburg Academy (dates in Russia at this time were still on Julian Calendar)
This value, which Euler approximated to 16 decimal places, 1.2020569031595942, is named Apery'a constant after Roger Apéry, who proved in 1978 that it is irrational. No other odd Zeta(n) has been proven either rational or irrational. It is still not known if it is transcendental. *Wik
1852 Massachusetts becomes the first state to pass a compulsory attendance law for school children. *VFR
1896, the Supreme Court ruled separate-but-equal facilities constitutional on intrastate railroads. For some fifty years, the Plessy v. Ferguson decision upheld the principle of racial segregation. Across the country, laws mandated separate accommodations on buses and trains, and in hotels, theaters, and schools.
In a speech delivered in the Ohio House of Representatives in 1886 and later published as The Black Laws, legislator Benjamin W. Arnett described life in segregated Ohio:
"This foe of my race stands at the school house door and separates the children, by reason of 'color,' and denies to those who have a visible admixture of African blood in them the blessings of a graded school and equal privileges... We call upon all friends of 'Equal Rights' to assist in this struggle to secure the blessings of untrammeled liberty for ourselves and posterity. "
1901 Charles Sanders Peirce writes George A. Plimpton, head of Ginn and Company and famous collector of rare mathematical books, describing what the contents of a newly acquired book must be were it indeed the great Liber Abaci (1202) of Fibonacci. In 1949 Carolyn Eisele’s discovery of this letter—still tucked into the back cover of the volume—began her career as a Peirce scholar. [HM 9, 335] *VFR (I have been advised by Adam Shapiro that Plimpton was not head of Ginn & Co until the death of Edwin Ginn in 1914.)
In 1910, Halley's Comet was visible from Earth, moving across the face of the sun. *TIS
1910 Halley's comet was big news during its visible period in New York City. Beginning with the Saturday edition of May 14 and continuing on through the Sunday edition of May 22, the comet was given top billing in the New York Times. This was the period when the comet was at the height of its brilliance and activity and the coverage clearly reflected this.
May 18: Earth to pass through come tail for 6 hours; C.B. Harmon invites college deans to join him in viewing comet from balloon. *Joseph M. Laufer, Halley's Comet Society - USA
1933 John Kieran’s Sports of the Times column in the New York Times is entitled “The Coordinate Clash, or Block that Abscissa.” The column was a humorous analogy between football and the upcoming mathematical contest between Harvard and Army. *VFR
It began with a poem called "A Logarithmic Lilt" which read:
"The Harvard horde is plotting, under cover of the dark, A fight to make the Crimson Chord subtend the Army arc. The Coefficient Corps has drilled with sharpened pencil tips And plans to drive the enemy away from the ellipse. The Harvard cry is 'Break the square and take the cube away!
While at the Point 'Abscissa' is the watchword of the day. And high upon the turret top the sentry turns his head And hears the Cambridge legion come with logarithmic tread. 'Advance and give the cosine!' rings the challenge through the air.
The Crimson host advances-and we hope the fight is fair." Later in the article, Kieran mentions the role of Lieutenant C. P. Nicholas, later head of the Mathematics Department, and Lieutenant Robinson as the Army coaches of the Analytics and Calculus, respectively. Other articles in newspapers continued the football analogy as their headlines read "Army Meets Harvard in Mathematical 'Go'," Squads at West Point Begin Contest in Calculus and Analytic Geometry," and "Harvard and West Point Line up on the Geometry Field."
1952 Prof. Willard F. Libby determined the age of Stonehenge on Salisbury Plain, England, at about 1848 BC (+/- 275 years) through analysis of the carbon-14 radioisotope in charcoal remains excavated there there. Update of C-14 ceases when plants or animals die, and the proportion in the organic remains steadily declines through radioactive decay. Since the half-life of C-14 is about 5,600 years, measurement of the remaining proportion in dead organic matter, indicates the age of that sample. Astronomer Sir Joseph Norman Lockyer had previously calculated that on Midsummer Day, 1680 BC, the sun rose directly over a special marking notch that can still be seen on the Heel Stone. Libby's measurements support that estimate. *TIS
1969, the Apollo 10 was launched to be a complete staging of the Apollo 11 mission without actually landing on the Moon. The mission was the second to orbit the Moon and the first to travel to the Moon with the entire Apollo spacecraft configuration. It made a successful eight-day dress rehearsal for the first manned moon landing. Astronauts Thomas Stafford and Eugene Cernan descended inside the Lunar Module to within 14 kilometers of the lunar surface (achieving the closest approach to the Moon before Apollo 11 landed two months later). Apollo 10 splashed down at 12:52 pm on 26 May, less than 4 miles (6.4 km) from the target point and the recovery ship
1610 Stefano della Bella, an Italian artist and engraver, was born May 18, 1610. When della Bella was barely twenty-one years old, he was commissioned to design and etch the frontispiece to Galileo’s Dialogue on the Two Chief World Systems (1632).
1850 Oliver Heaviside (18 May 1850, 3 Feb 1925) English physicist who predicted the existence of the ionosphere. In 1870, he became a telegrapher, but increasing deafness forced him to retire in 1874. He then devoted himself to investigations of electricity. In 1902, Heaviside and Kennelly predicted that there should be an ionised layer in the upper atmosphere that would reflect radio waves. They pointed out that it would be useful for long distance communication, allowing radio signals to travel to distant parts of the earth by bouncing off the underside of this layer. The existence of the layer, now known as the Heaviside layer or the ionosphere, was demonstrated in the 1920s, when radio pulses were transmitted vertically upward and the returning pulses from the reflecting layer were received. *TIS He adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations (later found to be equivalent to Laplace transforms), reformulated Maxwell's field equations in terms of electric and magnetic forces and energy flux, and independently co-formulated vector analysis. Although at odds with the scientific establishment for most of his life, Heaviside changed the face of mathematics and science for years to come. Among many others, he coined the terms for admittance , conductance , impedance , permeability , and inductance. *Wik
Much later Heaviside was honored in a far more enduring fashion--he became a phrase in an Andrew Lloyd Webber musical. In the climax of Cats the Musical, Grizabella is chosen by Old Deuteronomy to ascend to cat paradise and be reborn, while the feline chorus sings: "Up, up, up, past the Russell Hotel; up, up, up, up to the Heaviside layer" . The Heaviside layer (NOT the Kennelly-Heaviside layer) became for Webber (and Cats) a metaphor for heaven. Linda Hall Org
1853 Albert Badoureau (May 18, 1853, July 20, 1923) discovered 37 of the 75 non-prismatic uniform polyhedra in 1878. These were in addition to the 22 known at the time (5 Platonic solids, 13 Archimedean solids, and 4 Kepler-Poinsot polyhedra). He is also famed for his work in geology and for being the mathematical advisor to Jules Verne.
1872 Bertrand Russell. 3rd Earl Russell, OM, FRS (18 May 1872 – 2 February 1970), was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life, he imagined himself in turn a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things, in any profound sense. He was born in Wales, into one of the most prominent aristocratic families in Britain.
Russell led the British "revolt against idealism" in the early 1900s. He is considered one of the founders of analytic philosophy along with his predecessor Gottlob Frege and his protégé Ludwig Wittgenstein, and is widely held to be one of the 20th century's premier logicians. He co-authored, with A. N. Whitehead, Principia Mathematica, an attempt to ground mathematics on logic. His philosophical essay "On Denoting" has been considered a "paradigm of philosophy." His work has had a considerable influence on logic, mathematics, set theory, linguistics, and philosophy, especially philosophy of language, epistemology, and metaphysics. *Wik (on page 378 they are able to outline a proof for 1+1=2, but first they need to define the operation of addition.... then along comes Kurt Godel)
I include here a quote from his autobiography that is often shortened so that, what I believe was the critical last part of it, is not told:
At the age of eleven, I began Euclid, with my brother as my tutor. This was one of the great events of my life, as dazzling as first love. I had not imagined that there was anything so delicious in the world. After I had learned the fifth proposition, my brother told me that it was generally considered difficult, but I had found no difficulty whatever. This was the first time it had dawned upon me that I might have some intelligence. From that moment until Whitehead and I finished Principia Mathematica, when I was thirty-eight, mathematics was my chief interest, and my chief source of happiness. Like all happiness, however, it was not unalloyed. I had been told that Euclid proved things, and was much disappointed that he started with axioms. At first I refused to accept them unless my brother could offer me some reason for doing so, but he said: 'If you don't accept them we cannot go on', and as I wished to go on, I reluctantly admitted them pro tem. The doubt as to the premisses of mathematics which I felt at that moment remained with me, and determined the course of my subsequent work.
1889 Thomas Midgley Jr. (May 18, 1889 – November 2, 1944) was an American mechanical and chemical engineer. He played a major role in developing leaded gasoline (tetraethyl lead) and some of the first chlorofluorocarbons (CFCs), better known in the United States by the brand name Freon; both products were later banned from common use due to their harmful impact on human health and the environment. He was granted more than 100 patents over the course of his career.[2]
1941 Malcolm Sim Longair (18 May 1941 - )Scottish astronomer, noted for his scholarship and teaching, who in 1980 was appointed by Royal Warrant Astronomer Royal for Scotland, a post he held until 31 Dec 1990. The title of Astronomer Royal for Scotland was created in 1834. As Jacksonian Professor of Natural Philosophy and head of Cavendish Laboratory at the University of Cambridge, UK, his research interests include the emission from dust in the distant universe, observational cosmology, galaxy formation, and gravitational lensing. He is the current Public Understanding of Physics Fellow of the Institute of Physics. *TIS
1944 James Greig Arthur CC FRSC FRS (born May 18, 1944) is a Canadian mathematician working on automorphic forms, and former President of the American Mathematical Society. He is a Mossman Chair and University Professor at the University of Toronto Department of Mathematics.Arthur taught at Yale from 1970 until 1976. He joined the faculty of Duke University in 1976. He has been a professor at the University of Toronto since 1978. He was four times a visiting scholar at the Institute for Advanced Study between 1976 and 2002.
1946 Dame Celia Mary Hoyles, DBE, FAcSS, FIMA (née French; born 18 May 1946) is a British mathematician, educationalist and Professor of Mathematics Education at University College London (UCL), in the Institute of Education (IoE).
2007 Pierre-Gilles de Gennes French physicist who was awarded the 1991 Nobel Prize for Physics for "discovering that methods developed for studying order phenomena in simple systems can be generalized to more complex forms of matter, in particular to liquid crystals and polymers." He described mathematically how, for example, magnetic dipoles, long molecules or molecule chains can under certain conditions form ordered states, and what happens when they pass from an ordered to a disordered state. Such changes of order occur when, for example, a heated magnet changes from a state in which all the small atomic magnets are lined up in parallel to a disordered state in which the magnets are randomly oriented. Recently, he has been concerned with the physical chemistry of adhesion. *TIS
Credits:
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell


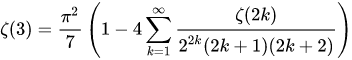





.jpg)























No comments:
Post a Comment