The shortest path between two truths in the real domain passes through the complex domain.
~Jacques Salomon Hadamard
The 236th day of the year; 236 is the sum of twelve consecutive primes, 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41
Since 236/4 = 59, 236 = 60^2 - 58^2.
The sum of the divisors of 236, 2+2 + 59 =63, the product of it's digits is 2x3x6 = 36, the reversal of the sum of the divisors.*Prime Curios
236^2 + 1 is a prime
236 is the average of two consecutive primes 233 and 239.
236 is a Happy Number. The sum of the squares of the digits under iteration go to 1.
And 236 is the number of possible positions in Othello after 2 moves by both players. *Erich Friedman (Students might try to figure out how many possible positions are there in tic-tac-toe after 2 moves by each player. Entice them with this number fact from Cliff Pickover @pickover )
79 Thousands were killed when the cities of Pompeii and Herculaneum were buried by the eruption of Mount Vesuvius.*VFR An estimated 20,000 people died. When discovered, the sites became astonishing archaeological time capsules.
Vesuvius has erupted many times since. It is the only volcano on Europe's mainland to have erupted in the last hundred years. It is regarded as one of the most dangerous volcanoes in the world
 |
| Mount Vesuvius as seen from the ruins of Pompeii*Wik |
1563 Tycho Brahe watched a spectacular conjunction of Jupiter and Saturn, and found that the time of the closest approach was days away from the predictions in the Ptolemaic Tables. He emerged from the experience with a life long passion for accuracy and exactitude and a devotion to the verdict of the sky. *Timothy Ferris, Coming of Age in the Milky Way
A great conjunction is a conjunction of the planets Jupiter and Saturn, when the two planets appear closest together in the sky. Great conjunctions occur approximately every 20 years when Jupiter "overtakes" Saturn in its orbit.
 |
| Near conjunction, Dec 16, 2020 *Wik |
1609 Galileo presented this telescope to the Doge in the Presence Chamber of the Doge's Palace and was confirmed in the professorship for life with his salary doubled! [Letter of 29 Aug 1609 from Galileo to his brother‑in‑law in Florence, quoted in Fahie, pp. 82‑83.] '... an object which is at a distance of nine miles will appear as if it were only one mile away, ... one can detect ships and sails of the enemy at sea ... we can see him two or more hours earlier than he can possibly see us, ....' [Galileo's letter to the Doge on 24 Aug 1609, quoted in Scandone, pp.12‑14 ; in Van Helden, pp. 7-8]. Through the connections of his friend Paolo Sarpi, Galileo presents an eight-powered telescope to the Venetian Senate. He is rewarded by a doubling of his salary and life- tenure at the University of Padua. He is disappointed by the fine print. *Galileo Project (I love the idea that the Greek name "telescope" was created by an actual Greek mathematician. It was created in 1611 by the Greek mathematician Giovanni Demisiani for one of Galileo Galilei's instruments presented at a banquet at the Accademia dei Lincei.)
1654 Pascal wrote a letter to Fermat, discussing Fermat’s solution to the “problem of points.”
I was not able to tell you my entire thoughts regarding the problem of the points
by the last post,and at the same time, I have a certain reluctance at doing it for fear lest
this admirable harmony which obtains between us and which is so dear to me should
begin to flag, for I am afraid that we may have different opinions on this subject. I
wish to lay my whole reasoning before you, and to have you do me the favor to set me
straight if I am in error or to indorse me if I am correct. I ask you this in all faith and
sincerity for I am not certain even that you will be on my side.
When there are but two players, your theory which proceeds by combinations is
very just. But when there are three, I believe I have a proof that it is unjust that you
should proceed in any other manner than the one I have. But the method which I
have disclosed to you and which I have used universally is common to all imaginable
conditions of all distributions of points, in the place of that of combinations (which I do
not use except in particular cases when it is shorter than the general method), a method
Which is good only in isolated cases and not good for others.
I am sure that I can make it understood, but it requires a few words from me and a
little patience from you. (I wish I had known this phrase early in my teaching career… it seems it would have been frequently useful)
*http://www.york.ac.uk/depts/maths/histstat/pascal.pdf
1731 Darwin receives a letter from his old teacher, J S Henslow, that will change his life: "I have been asked by Peacock who will read & forward this to you from London to recommend him a naturalist as companion to Capt Fitzroy employed by Government to survey the S. extremity of America— I have stated that I consider you to be the best qualified person I know of who is likely to undertake such a situation— I state this not on the supposition of yr. being a finished Naturalist, but as amply qualified for collecting, observing, & noting any thing worthy to be noted in Natural History." *DarwinProject
1775 Imen, Vtin, Caapan... Now you can count to three in the language of the native Americans living around Angel Island in San Francisco Bay. On this date the ship carrying Fr. Vicnete Maria, who spoke several native languages quite fluently interviewed them and recorded their responses for counting to 14. Later records of similar interviews in nearby regions match up very well to support the authenticity of this earliest known record of Native American numbers in the west. *Barbanabas Hughes. The priest accompanied explorer Juan de Ayala on the first Spanish naval entry aboard the San Carlos into the San Francisco Bay. On 12 August 1775, Ayala gave the name Isla de Alcatraces, "island of the pelicans ", and what is now Yerba Buena Island, "on account of the abundance of those birds that were on it." The name was transferred in 1826 to Alcatraz Island. The word "Alcatraz" comes from Spanish, which in turn was a probably a loan word from Arabic, القطرس al-qaṭrās meaning "sea eagle." The pelicans native to San Francisco Bay are brown pelicans.
One account is of just that. One of the scientists DID pass out at about 35,000’. Fortunately, the other was able to open the upper vent. *Tim Hamilton
In 1853, it has been claimed that the first potato chips were prepared by Chef George Crum, an American Indian, at Moon's Lake House in Saratoga Springs, NY. When railroad magnate Commodore Cornelius Vanderbilt was dining there, he sent his fried potatoes back to the kitchen, complaining they were "too thick." The chef, George Crum retaliated by slicing paper thin strips of potatoes and frying them to a crisp. But Vanderbilt loved these "Saratoga Chips" and they became an instant success.* TiS
1931 Oh Yes, They really did! Time Magazine published a story about a minister/University President who had trisected the angle, Rev. Jeremiah Joseph Callahan declared, "the problem can easily be solved by plane geometry." The conjecture from antiquity had been proved impossible in 1837, at least for mathematicians. I guess Lewis Carroll said it best,
"I daresay you haven't had much practice,' said the Queen. 'When I was your age, I always did it for half-an-hour a day. Why, sometimes I've believed as many as six impossible things before breakfast." *Ht to Dave Richeson@divbyzero in his Tales of Impossibility.
1971 The Soviet Union issued a stamp for the centenary of the birth of the British physicist, Ernest Rutherford. Beside his picture is a diagram of the movement of atomic particles which involves a hyperbola. [Scott #3888].*VFR
2006 And then there were only eight.... the International Astronomical Union decided to rescind Pluto’s status as a planet and reclassify it as another entity called a “dwarf planet”. *FFF, pg 537
I have been told that as early as 1980 at a celebration of the discovery, Brian Marsden, a long time opponent of Pluto as a planet, had said, "I will kill your Planet if it's the LAST thing I DO!". (I'm told this story is in :The Case for Pluto, by Alan Boyle)
 |
| New Horizons spacecraft captured this high-resolution enhanced color view of Pluto on July 14, 2015. *LOC |
She was born in Knudsturp, as the youngest of ten children, to Otte Brahe, advisor to the King of Denmark; and Beate Bille Brahe, leader of the royal household for Queen Sophie. Famous astronomer Tycho Brahe, 10 years her senior, was Sophie's oldest brother. When she was 17, she started assisting her brother with his astronomical observations in 1573, and helped him with the work that became the basis for modern planetary orbit predictions. She frequently visited his observatory Uranienborg, on the then-Danish island of Hveen. Tycho wrote that he had trained her in horticulture and chemistry, but he told her not to study astronomy. He expressed with pride that she learned astronomy on her own, studying books in German, and having Latin books translated with her own money so that she could also study them. Brother and sister were united by their work in science, and by their family's opposition to science as an appropriate activity for members of the aristocracy. Tycho referred with admiration to her 'animus invictus', her "determined mind" *Wik
 |
| Portrait from 1602 *Wik |
1561 Bartholomeo Pitiscus born. He coined the word “Trigonometry,” and first used it in print in 1595.*VFR Pitiscus achieved fame with his influential work written in Latin, called Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus (1595, first edition printed in Heidelberg), which introduced the word "trigonometry" to the English and French languages, translations of which had appeared in 1614 and 1619, respectively. It consists of five books on plane and spherical trigonometry. Pitiscus is sometimes credited with inventing the decimal point, the symbol separating integers from decimal fractions, which appears in his trigonometrical tables and was subsequently accepted by John Napier in his logarithmic papers (1614 and 1619).*Wik
1846 Professor Enoch Beery Seitz, the most distinguished mathematician of his day (Fairfield county, Ohio, August 24, 1846,- Kirksville, Missouri, October 8, 1883) He began his mathematical course in 1872 by contributing solutions to the problems proposed in the "Stairway" department of the Schoolday Magazine, conducted by Artemas Martin. His masterlv and original solutions to difficult Average and Probability problems, soon attracted universal attention among mathematicians. Dr. Martin, being desirous to know what works he had treating on that difficult subject, was greatly surprised to learn that he had no works upon the subject, but had learned what he knew about that difficult department of mathematical science by studying the problems and solutions in the Schoolday Magazine. He then contributed to the Analyst, the Mathematical Visitor, the Mathematical Magazine, the School Visitor, and the Educational limes, of London, England.
He took a mathematical course in the Ohio Wesleyan University in 1870, but did not finish it or graduate. In 1879,he was elected one of the teachers in the Greenville High School, which position he held till 1879. On the 24th of June, 1875, he married Miss Anna E. Kerlin, one of Dark county's most refined ladies. In 1879, he was elected to the chair of mathematics in the Missouri State Normal schlool, Kirksville, Missouri. During his first year as chair, he solved a problem posed by Professor Woolhouse in 1864 concerning the probability of firing a musket ball through the air at random. In the same vein, Seitz proposed a similar problem to the editor Artemis Martin in The Mathematical Visitor. Because of its difficulty, the problem received a great deal of attention and notoriety. Perhaps inspired by the Greenville hometown legend Annie Oakly and her rifleman ship, Seitz offered the problem:
"A cube is thrown into the air and a random shot fired through it; find the chance that the shot passes through the opposite side."
After nearly a year with no solutions forthcoming, Seitz published his own solution in The Mathematical Visitor:
On March the llth, 1880,he was elected a member of the London Mathematical Society, being the fifth American so honored.
He is often called "Teacher of the Great", for his many distinguished students: "When Professor Seitz went to Kirksville, in spite of the youth of the institution, he found an enthusiastic and capable body of students. He entered upon his work with his usual energy and the results of it are still felt throughout the country. He had in his class in algebra at one time, in the autumn of 1880, John J. Pershing who was destined to be the head of the armies of the United States In the World War, and Enoch Crowder who became head of the draft boards in the same conflict. He also had as a student at Kirksville. B F. Carroll, who later became governor of the state of Iowa, and John. R. Kirk who became president of the same institution in which he was then a student of Professor Seitz." *Obit in The Herald-Advertiser of Huntington, W.Va.
Seitz was elected to the London Mathematical Society on 11 March 1880, only the fifth American to be so honored. Over 500 of his solutions were published in the Analyst, the Mathematical Visitor, the Mathematical Magazine, the School Visitor and the Educational Times of London, England.
1894 Rudolf Oskar Robert Williams Geiger (24 Aug 1894, 22 Jan 1981) German meteorologist, one of the founders of microclimatology, the study of the climatic conditions within a few metres of the ground surface. His observations, made above grassy fields or areas of crops and below forest canopies, elucidated the complex and subtle interactions between vegetation and the heat, radiation, and water balances of the air and soil.*TIS
1917 Ralph Eugene Lapp (August 24, 1917 – September 7, 2004) was an American physicist who participated in the Manhattan Project.
Lapp was an American nuclear physicist and author who began his career in high-energy physics research with Arthur H. Compton. Lapp then worked at Chicago on the Manhattan Project. With 69 others, he signed Leo Szilard’s 17 Jul 1945 petition to President Truman, the month before the attack on Hiroshima. They urged that Japan should have an opportunity to surrender before use of the atom bomb. (Nevertheless, the actual attack was by surprise.) After the war, he researched the results in Japan. Lapp lectured across the U.S. He wrote 22 books on nuclear safety, including the dangers of nuclear fallout in The Voyage of the Lucky Dragon (1958). A Post book reviewer in 1956 called him “a one-man atomic truth squad and nuclear lie detector.”
1943 Karen Keskulla Uhlenbeck (born August 24, 1942) is an American mathematician and a founder of modern geometric analysis. She is a professor emeritus of mathematics at the University of Texas at Austin, where she held the Sid W. Richardson Foundation Regents Chair. She is currently a Distinguished Visiting Professor at the Institute for Advanced Study and a visiting senior research scholar at Princeton University.
Uhlenbeck won the 2019 Abel Prize for "her pioneering achievements in geometric partial differential equations, gauge theory, and integrable systems, and for the fundamental impact of her work on analysis, geometry and mathematical physics." She is the first woman to win the prize since its inception in 2003.
 |
| *Wik |
1595 Thomas Digges (1546?, 24 Aug 1595)
English astronomer and mathematician who (with his father, Leonard) was a pioneer in the use of the telescope. He was the leader of the English Copernicans. His observations of the new star of 1572, published in his Alae seu scalae mathematicae (1573) were second only to Tycho Brahe in accuracy. He used his observations of the supernova to justify the heliocentric system. In mathematics, he wrote on platonic and archimedian solids. *TIS After his father's death he was adopted and taught by John Dee. Digges was one of the first to translate (parts of) Copernicus into English. *Renaissance Mathematicus His father, Leonard Diggs, was also a fine mathematician, and often cited as the inventor (and namer) of the theodolite.
Thomas was the first to expound the Copernican system in English but discarded the notion of a fixed shell of immovable stars to postulate infinitely many stars at varying distances; he was also first to postulate the "dark night sky paradox". *Wik
The dark night sky paradox, is an argument in astrophysics and physical cosmology that says that the darkness of the night sky conflicts with the assumption of an infinite and eternal static universe. In the hypothetical case that the universe is static, homogeneous at a large scale, and populated by an infinite number of stars, any line of sight from Earth must end at the surface of a star and hence the night sky should be completely illuminated and very bright. This contradicts the observed darkness and non-uniformity of the night.
1670 William Neile (7 December 1637 – 24 August 1670) was an English mathematician and founder member of the Royal Society. His major mathematical work, the rectification of the semicubical parabola ( \(y^3 = a x^2\) ), was carried out when he was aged nineteen, and was published by John Wallis who was his teacher. By carrying out the determination of arc lengths on a curve given algebraically, in other words by extending to algebraic curves generally with Cartesian geometry a basic concept from differential geometry, it represented a major advance in what would become infinitesimal calculus. His name also appears as Neil.
Neile was the first to calculate the length of the semi-cubical parabola. It was discovered (created?) by William Neile in 1657. It was the first algebraic curve to have its arc length computed. Wallis published the method in 1659 giving Neile the credit.
1739 Takebe Katahiro was a Japanese mathematician who wrote most of Seki's Encyclopaedia.*SAU
1796 (Nicholas Léonard) Sadi Carnot (born 1 Jun 1796, 24 Aug 1832) was a French physicist. He became a captain of engineers in the army, and spent much of his life investigating the design of steam engines. His book Reflections on the Motive Power of Heat (1824) contained a theorem which says that a maximum efficiency of heat engine can be obtained by a reversible engine, and that efficiency depends only on the temperatures of the hot and the cool sources of the engine. This theorem played an essential role for the subsequent development of thermodynamics. It was written to promote the construction of steam engines and other heat engines in France, whose industrial development was lagging behind England's. *TIS
1842 Benjamin Wright (10 Oct 1770, 24 Aug 1842)American engineer who directed the construction of the Erie Canal. A one-time judge, he helped survey the Erie Canal route. When the Erie Canal was finally funded in 1817, Wright was selected as one of the three engineers to design and build it, then named chief engineer. Wright made the Erie Canal project a school of engineering. Until mid-century, almost every civil engineer in the U.S. had trained with, or been trained by someone who had worked under, Wright on the Erie Canal. Because he trained so many engineers on that project, Wright has been called the "father of American civil engineering." He also engaged in the design and construction at the outset of the first railroads. He was the first Chief Engineer of the Erie Railroad.*TIS
1888 Rudolf (Julius Emanuel) Clausius (2 Jan 1822, 24 Aug 1888) was a German mathematical physicist who formulated the second law of thermodynamics and is credited with making thermodynamics a science. Essentially a theoretical physicist, he published his work in thermodynamics in 1865 wherein he stated the First and Second laws of thermodynamics in the following form: (1) The energy of the universe is constant. (2) The entropy of the universe tends to a maximum. In all Clausius wrote eight important papers on the topic. He restated Sadi Carnot's principle of the efficiency of heat engines. The -Clapeyron equation expresses the relation between the pressure and temperature at which two phases of a substance are in equilibrium. *TIS
1971 Wallace John Eckert (June 19, 1902 – August 24, 1971) was an American astronomer, who directed the Thomas J. Watson Astronomical Computing Bureau at Columbia University which evolved into the research division of IBM.
He started teaching at Columbia University in 1926, and earned his PhD from Yale in 1931 in astronomy under Professor Ernest William Brown (1866–1938).
Around 1933 Eckert proposed interconnecting punched card tabulating machines from IBM located in Columbia's Rutherford Laboratory to perform more than simple statistical calculations. Eckert arranged with IBM president Thomas J. Watson for a donation of newly developed IBM 601 calculating punch, which could multiply instead of just adding and subtracting.[6] In 1937 the facility was named the Thomas J. Watson Astronomical Computing Bureau. IBM support included customer service and hardware circuit modifications needed to tabulate numbers, create mathematical tables, add, subtract, multiply, reproduce, verify, create tables of differences, create tables of logarithms and perform Lagrangian interpolation, all to solve differential equations for astronomical applications. In January 1940, Eckert published Punched Card Methods in Scientific Computation, which solved the problem of predicting the orbits of the planets, using the IBM electric tabulating machines, based on the punched card. This slim book is only 136 pages, including the index.
In 1940, Eckert became director of the United States Naval Observatory in Washington, D.C. World War II had been raging in Europe for many months. The US had not yet officially joined the effort to defeat Hitler. Nonetheless, the demand for navigation tables had risen. This demand helped inspire Eckert to automate the process of creating these tables, using punched card equipment. The 1941 almanac was the first to be produced using automated equipment, down to the final typesetting. Martin Schwarzschild became directory of the Columbia laboratory while Eckert was at USNO.
After the war Eckert moved back to Columbia. Watson had just had a falling out with Harvard University over a project IBM had funded. IBM would instead focus their funding on Columbia, and Eckert's laboratory was named Watson Scientific Computing Laboratory. Eckert understood the significance of his laboratory, keenly aware of the advantage of scientific calculations performed without human interventions for long stretches of computation. A massive machine built to Eckert's specifications was built and installed behind glass at IBM's headquarters on Madison Avenue in January 1948. Known as the Selective Sequence Electronic Calculator, it was used as a calculating device with some success, but served even better as a recruiting tool.[11] Eckert published a description of the SSEC in November 1948.[12]
As an employee of IBM, Eckert directed one of the first industrial research laboratories in the country. In 1945 he hired Herb Grosch and Llewellyn Thomas as the next two IBM research scientists, who both made significant contributions. When Cuthbert Hurd became the next PhD to be hired by IBM in 1949, he was offered a position with Eckert, but instead founded the Applied Science Department, and later directed the development of IBM's first commercial stored program computer (the IBM 701) based on the demand demonstrated by applications such as those of Eckert.
In this period he continued his innovative contributions to computational astronomy by implementing Brown's Lunar theory in his computer; developing the Improved Lunar Ephemeris; and performing the first numerical integration to compute an ephemeris for the outer planets.
In 1957 the Watson lab moved to Yorktown Heights, New York (with a new building completed in 1961) where it is known as the Thomas J. Watson Research Center. Eckert won the James Craig Watson Medal in 1966 from the US National Academy of Sciences.
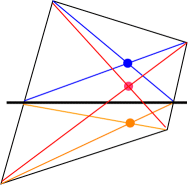
1975 Anna Margaret Mullikin (March 7, 1893 - August 24, 1975) She was born in Baltimore, Maryland and attended Goucher College, which was then a women's college located in the same city. While there she managed her class basketball team, participated on the swimming team, and earned her A.B. degree in 1915. That same year her name was mentioned in the American Mathematical Monthly [Vol. 22, No. 5 (May 1915),pp. 165-166] for solving the following geometry problem:
A quadrilateral of any shape whatever is divided by a transversal into two quadrilaterals. The diagonals of the original figure and those of the two resulting (smaller) figures are then drawn. Show that their three points of intersection are collinear.In 1918 she entered the graduate program in mathematics at the University of Pennsylvania, earning her master's degree in 1919. She continued her graduate studies at Penn during the 1919-1920 academic year under the direction of the topologist, Robert L. Moore, while also teaching at the Stevens School in Germantown, Pennsylvania, another private preparatory school for girls. In the fall of 1920 she moved to the University of Texas along with Moore, who had convinced the Texas math department to appoint her as an instructor. Mullikin stayed in Texas for only the one academic year before returning to Philadelphia to complete the requirements for her degree from the University of Pennsylvania, with Moore still as her advisor. She received her Ph.D. in mathematics in 1922. Mullikin did not pursue mathematical research after earning her Ph.D. She spent the rest of her professional career as a high school mathematics teacher, first at William Penn High School for Girls in Philadelphia for one year, and then at Germantown High School where she remained until her retirement in 1959. She was appointed head of the mathematics department in 1952. In 1956 she was a joint author with Ethel and Ewart Grove for the textbook Algebra and Its Use. *Agnes Scott College (One wonders who was (or were) the Dept Head for the almost 30 years this female PhD served before she got the position.)
The published solution was by Vola Barton, also from Goucher College, with the remark "Also solved by Anna Mullikin."
1982 Giorgio Abetti (5 Oct 1882,24 Aug 1982)Italian astronomer known for his studies of the sun at the University of Padua where was director at the Arcetri Observatory (1921-52), taking over from his father who also held the post (1894-1921). In 1913, Giorgio Abetti took part, as a geodetic and geophysical astronomer, in the De Filippi expedition in Karakorum, Himalaya and Turkestan. He went on expeditions to observe eclipses of the sun, including one to Siber
ia to observe the total eclipse on 19 Jun 1936 and in 1952 to Sudan. With the advice of George Hale, he built a solar tower at the observatory (opened 1925). He wrote a popular text on the sun, a handbook of astrophysics (1936) and a popular history of astronomy (1963).*TIS
1997 Louis Essen (6 Sep 1908, 24 Aug 1997 )English physicist who invented the quartz crystal ring clock and the first practical atomic clock. These devices were capable of measuring time more accurately than any previous clocks. He built a cesium-beam atomic clock, a device that ultimately changed the way time is measured. Each chemical element and compound absorbs and emits electromagnetic radiation at its own characteristic frequencies. These resonances are inherently stable over time and space. The cesium atom's natural frequency was formally recognized as the new international unit of time in 1967: the second was defined as exactly 9,192,631,770 oscillations or cycles of the cesium atom's resonant frequency, replacing the old second defined in terms of the Earth's motion. *TIS
Louis Essen (right) and Jack Parry (left) standing next to the world's first caesium-133 atomic clock.*Wik
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
No comments:
Post a Comment