"I have finally found a subject where I do not need to memorize, but can think things out myself – mathematics."
~Herta Taussig Freitag (from her diary, age 12)
The 340th day of the year; 340 is the sum of the first four powers of four.
340 can also be written as the sum of consecutive primes in three different ways.
340! +1 is prime. There are only thirteen day numbers of the year for which n! +1 is prime, and 340 is the last of these.
Jim Wilder@wilderlab pointed out that 340 = 41 + 42 + 43 + 44. Just think, tomorrow will be even a longer string of consecutive powers of four!
1586 Jesuit astronomer, Niccolò Zucchi, the first to attempt to build a reflecting telescope was born 6 December 1586. In his Optica philosophia experimentis et ratione a fundamentis constituta published in 1652 he describes his attempt to create a reflecting telescope.*Thony Christie
As an astronomer he may have been the first to see the belts on the planet Jupiter (on May 17, 1630), and reported spots on Mars in 1640.
His "Optica philosophia experimentis et ratione a fundamentis constituta", published in 1652–56, described his 1616 experiments using a curved mirror instead of a lens as a telescope objective, which may be the earliest known description of a reflecting telescope. In his book he also demonstrated that phosphors generate rather than store light. He also published two other works on mechanics and machines.
In 1623, Zucchi was a member of a Papal legate sent to the court of Ferdinand II. There he met Johannes Kepler, the German mathematician and astronomer. Kepler encouraged Zucchi's interest in astronomy. Zucchi maintained correspondence with Kepler after returning to Rome. At one point when Kepler was in financial difficulties, Zucchi, at the urging of the Jesuit scientist Father Paul Guldin, gave a telescope of his own design to Kepler, who mentioned the gift in his book “The Dream”.
 |
| *Linda Hall Org |
1592, Galileo was appointed Professor of Mathematics at the University of Padua (the University of the Republic of Venice) at a salary of three times that he had received at Pisa. On 7 December 1592 he gave his inaugural lecture and began a period of 18 years at the University, years which he later described as the happiest of his life. *British Journal of Sports Medicine (honest)
In 1631, the transit of Venus occurred as first predicted by Kepler. He correctly predicted that an ascending node transit of Venus would occur in Dec 1631, but no-one observed it - due to the fact that it occurred after sunset for most of Europe. Kepler himself died in 1630. He not only predicted this particular transit but also worked out that transits of Venus involve a cyclical period of approximately 120 years. When such a transit is observed, Venus appears as a small black circle moving across the face of the Sun.*TIS Kepler had predicted transits in 1631 and 1761 and a near miss in 1639. Horrocks corrected Kepler's calculation for the orbit of Venus, realized that transits of Venus would occur in pairs 8 years apart, and so predicted the transit of 1639. *Wik
1710 An advertisement in the Old Bailey Proceedings for a book on mathematics, and more
*** The Marrow of the Mathematicks, made Plain and Easie to the Understanding of any ordinary Capacity. Containing the Doctrines of Arithmetick, Geometry, Astronomy, Gauging, the Use of the Sector, Surveying, Dyaling, and the Art of Navigation, &c. Illustrated with several Cuts, for the better Explanation of the whole Matter. After a New, Compendious, Easy Method By W. Pickering, Merchant-Adventurer.
To which is added,
Measuring Surfaces and Solids, such as Plank, Timber, Stone, &c. Joiners, Carpenters, Bricklayers, Glasiers, Painters and Paviers Work: Each Proposition being wrought Vulgarly, Decimally, Practically and Instrumentally. With a small Tract of Gauging Wine, Ale, or Malt, without Inches, or Division; by which any one may Gauge ten Backs or Floors of Malt, in the same time another shall Guage one, by the Way now used. Altogether New, and submitted to the Censure of the Honourable Commissioners of Excise. By J. L. P. M.
Both Printed for Eben. Tracy, at the Three Bibles on London-Bridge. 1710
 |
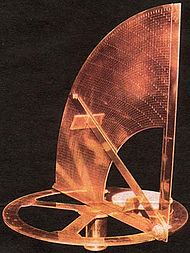| Pedro Nunes Nonius original model |
1763 From Charles Mason's Journal of the Mason Dixon survey, "Set up a Sector brought by the Commissioners from Maryland and found that the nonius would not touch the middle part of the arch" A nonius is a device, named in honor to its author and inventor Pedro Nunes (Latin: Petrus Nonius), created in 1542 as a system for taking fine measurements on the astrolabe which could largely improve its accuracy. Later on, it was adapted in 1631 by the French mathematician Pierre Vernier, to create the vernier scale. *Wik
1778 Joseph Louis Gay-Lussac,(6 December 1778 – 9 May 1850)) a French chemist, is well known to modern chemists for two laws, one relating the volume of a gas to its temperature (volume increases linearly with temperature), and the second, called the law of combining volumes, which states that when two gases combine, their volumes are in the ratios of small whole numbers. This latter law, announced in 1808, demonstrated, for example, that when one combines hydrogen and oxygen to form water, it takes exactly two volumes of hydrogen for every one volume of oxygen. The law of combining volumes could be used to support John Dalton's atomic theory, published the very same year, for if water consists of two atoms of hydrogen and one of oxygen, then one might well expect that you would need two volumes of hydrogen for every one of oxygen (assuming that equal volumes of gases contain equal numbers of particles, and Amadeo Avogadro would offer this up as his own law, Avogadro's hypothesis, in 1811).
For the non-chemist, Gay-Lussac's career as a balloonist might be of more interest. With fellow chemist Jean-Baptiste Biot, Gay-Lussac made a balloon ascent of some 4 miles in 1804, collecting atmospheric samples all the way, and the next year he made a solo ascent and went even higher, setting an altitude record of some 23,000 feet that would stand for another 60 years. He also determined that the composition of the atmosphere does not change with altitude.
In 1867, Louis Figuier published an image of the Biot/Gay-Lussac ascent that has proved quite enduring in ballooning lore ; the illustration has been much copied, even appearing on a tea card . Gay-Lussac has also been featured on a French postage stamp . He was buried in the famous Père Lachaise cemetery in Paris . *Linda Hall Org
1830 First national observatory established at Washington, D.C. Established by the order of the Secretary of the Navy, John Branch, on 6 December 1830 as the Depot of Charts and Instruments, the Observatory rose from humble beginnings. Placed under the command of Lieutenant Louis M. Goldsborough, with an annual budget of 330 US Dollars, its primary function was the restoration, repair, and rating of navigational instruments. It was made into a national observatory in 1842 via a federal law and a Congressional appropriation of 25,000 dollars. Lieutenant James Melville Gilliss was put in charge of "obtaining the instruments needed and books." *Wik (Interestingly, Goldsborough was appointed to the Naval Academy at the age of seven, although he did not enter for several years. He rose to the rank of Admiral during the U S Civil War and three naval ships were named for him.)
1882 Venus crossed the disc of the Sun. The most recent transit of Venus when observed from Earth took place on June 8, 2004. The event received significant attention, since it was the first Venus transit to take place after the invention of broadcast media. No human alive at the time had witnessed a previous Venus transit. The next transit of Venus will occur on June 5–June 6 in 2012,. After 2012, the next transits of Venus will be in December 2117 and December 2125.*Wik
The transit of Venus across the sun was photographed on a series of glass plate negatives made by Amherst College astronomer David Peck Todd. He used a solar photographic telescope (made by the renowned optical firm Alvan Clark & Sons) stationed on the summit of Mount Hamilton, California, where the Lick Observatory was under construction. Of the photos, 147 survived, having been archived in the mountain vault. A century later, they were retrieved and an animation made from them premiered at the International Astronomical Union's general assembly in Sydney in Jul 2003. This is perhaps the most complete surviving record of a historical transit of Venus, dating from the time when Chester Arthur was president of the United States.*TIS
An illustration of the transit of Venus of 1882. Ceiling mural in the Paris Observatory.
Dr. Russell Houser informed me that this transit led to the creation of John Phillip Sousa's Transit of Venus March.
One year after the 1882 Transit of Venus, Sousa was commissioned to compose a processional for the unveiling of a bronze statue of American physicist Joseph Henry, who had died in 1878. Henry, who had developed the first electric motor, was also the first secretary of the Smithsonian Institution in Washington, D.C.
A Freemason, Sousa was fascinated by what the group considered mystical qualities in otherwise natural phenomena. According to Sten Odenwald of the NASA IMAGE Science Center, this played a significant role in the selection of the time and date of the performance, April 19, 1883, at 4:00 P.M. Dr. Odenwald points out that Venus and Mars, invisible to the participants, were setting in the west. At the same time, the moon, Uranus, and Virgo were rising in the east, Saturn had crossed the meridian, and Jupiter was directly overhead. According to Masonic lore, Venus was associated with the element copper, a component of electric motors.
These kinds of connections seem to go on and on. Henry may well have influenced the writing of Moby Dick, in particular the shape of a kettle in one important passage in the book.
1882 Oliver Wendell Holmes Sr. was an MD, and professor of anatomy at Harvard. He was also a poet and novelist, and an amateur astronomer. He wrote the lines below after witnessing the Transit of Venus mentioned above in 1882 on Boston Commons:
He glares at me, I stare at him;And lo! my straining eye has foundA little spot that, black and round,Lies near the crimsoned fire-orb’s rim.O blessed, beauteous evening star,Well named for her whom earth adores,—The Lady of the dove-drawn car,—I know thee in thy white simar;But veiled in black, a rayless spot,Blank as a careless scribbler’s blot,Stripped of thy robe of silvery flame,—The stolen robe that Night restoresWhen Day has shut his golden doors,—I see thee, yet I know thee not;And canst thou call thyself the same?
------
And art thou, then, a world like ours,Flung from the orb that whirled our ownA molten pebble from its zone?How must thy burning sands absorbThe fire-waves of the blazing orb,Thy chain so short, thy path so near,Thy flame-defying creatures hearThe maelstroms of the photosphere!And is thy bosom decked with flowersThat steal their bloom from scalding showers?And hast thou cities, domes, and towers,And life, and love that makes it dear,And death that fills thy tribes with fear?
The Flâneur
BY OLIVER WENDELL HOLMES SR.
1917 Kazimierz Kuratowski gave a talk “On the definitions in mathematics,” which became his first published paper. This work grew out of Jan LLukasiewicz’s crushing criticism of the foundations of StanisLlaw Zaremba’s Theoretical Arithmetic (1912). Kuratowski’s now famous 1921 definition of ordered pair (a nice note for Alg classes) also grew out of LLukasiewicz’s critique. [Kuratowski, A Half Century of Polish Mathematics, p. 24] *VFR
The "Earliest Known Uses of Some of the Words of Mathematics " on MacTutor states, "ORDERED PAIR occurs in "A System of Axioms for Geometry," Oswald Veblen, Transactions of the American Mathematical Society, 5 (Jul., 1904): "Each ordered pair of elements determines a unique element that precedes it, a unique element that follows it and a unique middle element." Only 7 years before this formal definition.
1946 Birthdate of Nicolette Weil, younger daughter of the mathematician Andre Weil. She was born on St. Nicholas’ day, as he planned, or so he jokingly claimed, but she is named after Nicolas Bourbaki. Professor Weil was one of the founders of the Bourbaki group. See Joong Fang, Bourbaki, Paideia Press, 1970, p. 40. His older daughter is named Sylvie and was born 12 September 1942. *VFR
1956 The knapsack problem was first named and discussed by George B. Dantzig, the father of linear programming. *VFR (The part about naming it may be an error; the problem existed long before and *Wik has this note:) "The knapsack problem has been studied for more than a century, with early works dating as far back as 1897. (Mathews, G. B. (25 June 1897). "On the partition of numbers" (PDF). Proceedings of the London Mathematical Society. ) It is not known how the name "knapsack problem" originated,(they should read my blog?) though the problem was referred to as such in the early works of mathematician Tobias Dantzig (1884–1956)(This was George's Father), suggesting that the name could have existed in folklore before a mathematical problem had been fully defined."
Knapsack problems appear in real-world decision-making processes in a wide variety of fields, such as finding the least wasteful way to cut raw materials. selection of investments and portfolios, selection of assets for asset-backed securitization, and generating keys for the Merkle–Hellman and other knapsack cryptosystems.
 |
| *Wik |
In 1957, America's first attempt at putting a satellite into orbit failed when the Vanguard rocket carrying it blew up on the launch pad at Cape Canaveral, Florida. With a series of rumbles audible for miles around, the vehicle, having risen about four feet into the air, suddenly sank. Falling against the firing structure, fuel tanks rupturing as it did so, the rocket toppled to the ground on the northeast or ocean side of the structure in a roaring, rolling, ball-shaped volcano of flame. *TIS
1987 Florida rapist Tommy Lee Andrews is the first person to be convicted as a result of DNA fingerprinting. *Wik
2005 At a book signing after a mathematics professor at West Point was asked what he taught, former president Jimmy Carter commented “In retrospect, I possibly received the best insight into human nature by studying differential equations and systems of differential equations. That subject seemed to interrelate rates of change between interconnected entities.” *VFR
1586 Niccolò Zucchi (6 Dec 1586; 21 May 1670) Italian astronomer who, in approximately 1616, designed one of the earliest reflecting telescopes, antedating those of James Gregory and Sir Isaac Newton. A professor at the Jesuit College in Rome, Zucchi developed an interest in astronomy from a meeting with Johannes Kepler. With this telescope Zucchi discovered the belts of the planet Jupiter (1630) and examined the spots on Mars (1640). He also demonstrated (in 1652) that phosphors generate rather than store light. His book Optica philosophia experimentalis et ratione a fundamentis constituta (1652-56) inspired Gregory and Newton to build improved telescopes.*TIS(I belive the observations he made were NOT with his reflecting telescope, which never seemed to work, but with the more common refracting telescope. See more on reflecting telescopes at this blog where Thony Christie takes me to task for giving (too much) credit to one of the early developers.)
1682 Giulio Carlo Fagnano dei Toschi (December 6, 1682 – September 26, 1766) who was born in Sinigaglia, Italy. He was the founder of the geometry of the triangle, studied the lemniscate, and coined the term “elliptic integral.” *VFR
Fagnano is best known for investigations on the length and division of arcs of certain curves, especially the lemniscate; this seems also to have been in his own estimation his most important work, since he had the figure of the lemniscate with the inscription: "Multifariam divisa atque dimensa Deo veritatis gloria", engraved on the title-page of his Produzioni Matematiche, which he published in two volumes (Pesaro, 1750), and dedicated to Pope Benedict XIV. The same figure and words "Deo veritatis gloria" also appear on his tomb.
Failing to rectify the ellipse or hyperbola, Fagnano attempted to determine arcs whose difference should be rectifiable. He also pointed out the remarkable analogy existing between the integrals which represent the arc of a circle and the arc of a lemniscate. Finally he proved the formula π = 2i log((1-i)/(1+i)
One of his sons, Giovanni, is the namesake of the optimization problem called Fagnano's Problem in geometry :
For a given acute triangle determine the inscribed triangle of minimal perimeter.
The solution is the orthic triangle.
1848 Johann Palisa (6 Dec 1848; 2 May 1925) Silesian astronomer who was a prolific discoverer of asteroids, 122 in all, beginning with Asteroid 136 Austria (on 18 Mar 1874, using a 6” refractor) to Asteroid 1073 Gellivara in 1923 - all by visual observation, without the aid of photography. In 1883, he joined the expedition of the French academy to observe the total solar eclipse on May 6 of that year. During the eclipse, he searched for the putative planet Vulcan, which was supposed to circle the sun within the orbit of Mercury. In addition to observing the eclipse, Palisa collected insects for the Natural History Museum in Vienna. He also prepared two catalogs containing the positions of almost 4,700 stars. He remains the most successful visual discoverer in the history of minor planet research.*TIS
1856 Walther Franz Anton von Dyck (6 Dec 1856 in Munich, Germany - 5 Nov 1934 in Munich, Germany) Von Dyck made important contributions to function theory, group theory (where a fundamental result on group presentations is named after him) topology and potential theory. *SAU
1880 Pierre Léon Boutroux (6 December 1880 – 15 August 1922) was a French mathematician and historian of science. Boutroux is chiefly known for his work in the history and philosophy of mathematics.
He was born in Paris on 6 December 1880 into a well connected family of the French intelligentsia. His father was the philosopher Émile Boutroux. His mother was Aline Catherine Eugénie Poincaré, sister of the scientist and mathematician Henri Poincaré. A cousin, Raymond Poincaré was to be President of France.
He occupied the mathematics chair at Princeton University from 1913 until 1914. He occupied the History of sciences chair from 1920 to 1922.
Boutroux published his major work Les principes de l'analyse mathématique in two volumes; Volume 1 in 1914 and Volume 2 in 1919. This is a comprehensive view of the whole field of mathematics at the time.*Wik
1900 George Eugene Uhlenbeck (6 Dec 1900; 31 Oct 1988) Dutch-American physicist who, with Samuel A. Goudsmit, proposed the concept of electron spin (Jan 1925) - a fourth quantum number which was a half integer. This provided Wolfgang Pauli's anticipated "fourth quantum number." In their experiment, a horizontal beam of silver atoms travelling through a vertical magnetic field was deflected in two directions according to the interaction of their spin (either "up" or "down") with the magnetic field. This was the first demonstration of this quantum effect, and an early confirmation of quantum theory. As well as fundamental work on quantum mechanics, Uhlenbeck worked on atomic structure, the kinetic theory of matter and extended Boltzmann's equation to dense gases.*TIS
1907John Barkley Rosser Sr. (December 6, 1907 – September 5, 1989) is born in Jaksonville, FL. In 1934 Rosser received a Ph.D. in logic from Princeton under the supervision of Alonso Church. Rosser was able to anticipate the potential of early computers in many areas of mathematics as well as the ultimate impact of logic on the future of computing. He contributed to the Church-Rosser theorem that identifies the outer limit of what is achievable in automated theorem proving and, therefore, plays the same role in computing science as the second law of thermodynamics in engineering.
Rosser taug ht at Cornell and the University of Wisconsin, served as a president of the Association of Symbolic Logic and SIAM. He died on September 5, 1989. *CHM
1908 Herta Taussig Freitag (December 6, 1908 - January 25, 2000) Herta obtained a job at a private high school, the Greer School, in upstate New York. There she met Arthur H. Freitag and they were married in 1950. Herta started teaching at Hollins College (now University) in Roanoke, VA in 1948. She received a Ph.D. degree from Columbia University in 1953 and the title of her dissertation was "The Use of the History of Mathematics in its Teaching and Learning on the Secondary Level."
During Herta's years at Hollins she was a frequent guest speaker at local schools and gave lectures at both Virginia and North Carolina Governor's Schools. She published numerous articles in The Mathematics Teacher, The Arithmetic Teacher, and The Mathematics Magazine. At the request of the National Council of Teachers of Mathematics, Professor Freitag wrote the monograph, The Number Story, with her husband. In 1962 she was the first woman to be President of the Maryland-District of Columbia-Virginia Section of the Mathematical Association of America (MAA). Professor Freitag received the Hollins' Algernon Sydney Sullivan Award, which is awarded for recognition of "extraordinary humane and scholarly achievement." She officially retired from Hollins in 1971 to spend time with her husband, who was ill. After his death in 1978, Hollins welcomed her back to the classroom as a leave replacement in 1979-1980 and as a teacher in the Master of Arts in Liberal Studies (MALS) program for several years. Professor Herta Freitag was the first faculty member to receive the Hollins Medal (1979) and the first recipient of the Virginia College Mathematics Teacher of the Year award (1980).
Professor Freitag was very proud of her perfect attendance at the International Conferences of the Fibonacci Association. Most of her work with Fibonacci numbers occurred after she retired, which demonstrates the fallacy of a commonly held belief that mathematicians complete their best work before the age of 40. Professor Freitag published more than thirty articles in the Fibonacci Quarterly after 1985. The November 1996 issue of the Fibonacci Quarterly was dedicated to "Herta Taussig Freitag as she enters her 89th year, in recognition of her years of outstanding service and achievement in the mathematics community through excellence in teaching, problem solving, lecturing and research." This award was given to celebrate her 89th birthday, since 89 is a Fibonacci number. *Biographies of Women Mathematicians, Agnes Scott College web site
1916 John L. Kelley (December 6, 1916, Kansas – November 26, 1999, Berkeley, California) was an American mathematician at the University of California, Berkeley, who worked in general topology and functional analysis.
Kelley's 1955 text, General Topology, which eventually appeared in three editions and several translations, is a classic and widely cited graduate-level introduction to topology. An appendix sets out a new approach to axiomatic set theory, now called Morse–Kelley set theory, that builds on Von Neumann–Bernays–Gödel set theory. He introduced the first definition of a subnet.
After earning B.A. (1936) and M.A. (1937) degrees from the University of California, Los Angeles, he went to the University of Virginia, where he obtained his Ph.D. in 1940. Gordon Whyburn, a student of Robert Lee Moore, supervised his thesis, entitled A Study of Hyperspaces. He taught at the University of Notre Dame until the outbreak of World War II. From 1942 to 1945, he did mathematics (mainly exterior ballistics, including ballistics for the atomic bomb) for the war effort at the Aberdeen Proving Ground, where his work unit included his future Berkeley colleagues Anthony Morse and Charles Morrey. After teaching at the University of Chicago, 1946–47, Kelley spent the rest of his career at Berkeley, from which he retired in 1985. He chaired the Mathematics Department at Berkeley 1957–60 and 1975–80. He held visiting appointments at Cambridge University and the Indian Institute of Technology in Kanpur, India. An Indian mathematician, Vashishtha Narayan Singh, was among those mentored by Kelley.
In 1950, Kelley was one of 29 tenured Berkeley faculty (3 of whom were members of the Mathematics Department) dismissed for refusing to sign a McCarthy-era loyalty oath mandated by the UC Board of Regents. When asked why he refused to swear that he was loyal to his country, he replied, "For the same reason that I would refuse to swear, under duress, that I loved my mother." He then taught at Tulane University and the University of Kansas. He returned to Berkeley in 1953, after the California Supreme Court declared the oath unconstitutional and directed UC Berkeley to rehire the dismissed academics. He was later an outspoken opponent of the Vietnam War.
Kelley's interest in teaching extended well beyond the higher reaches of mathematics. In 1960, he took a leave of absence to serve as the National Teacher on NBC's Continental Classroom television program. He was an active member of the School Mathematics Study Group (SMSG), which played an important role in designing and promulgating the "new math" of that era. In 1964, he led his department to introduce a new major called Mathematics for Teachers, and later taught one of its core courses. These endeavors culminated in the text Kelley and Richert (1970). In 1977–78, he was a member of the U.S. Commission on Mathematical Instruction.*Wik
He described his youth this way: "For the first thirteen years of my life my family was not urban, nor suburban, but just country. We lived in small towns, the largest with fewer than 2500 inhabitants: the roads were unpaved, we had no radio and television hadn't been invented. I was born in my family's house (there was no hospital in town) ... I was a genuine, twenty-four-carat country boy, a vanishing breed in these United States." *SAU
1941 Filep László (6 Dec 1941 in Csaszlo, Szabolcs-Szatmar-Bereg, Hungary - 19 Nov 2004 in Budapest, Hungary) He worked for the degree of dr. univ. submitting his thesis Life and work of Gyula Farkas (1847-1930) to the Kossuth University in Debrecen in 1978. But this was not László's first publication, for he had published a number of articles in the prestigious Hungarian popular scientific magazine, Termeszet Vilaga (The World of Nature). The first of these articles was Farkas Gyula (1847-1930) published in 1976, was followed by A matematika nagy nöalakjai (1977) and Helyunk a tudomany vilagaban (1979). He published many other articles on the history of mathematics such as Lajos David (1881-1962), historian of Hungarian mathematics (1981), Great female figures of Hungarian mathematics in 19th-20th centuries (1983), The development, and the developing of the concept of a , fraction (2001), The genesis of Eudoxus's infinity lemma and proportion theory (2001), From Fejer's disciples to Erdős's epsilons - change over from analysis to combinatorics in Hungarian mathematics (2002), and Irrationality and approximation of √2 and √3 in Greek mathematics (2004). He also published biographies of many mathematicians including Janos Bolyai, John C Harsanyi, John von Neumann, and Paul Erdős. László's research interest was not only in the history of mathematics for he also published a long series of papers on fuzzy groups, some written with his collaborator Iulius Gyula Maurer, beginning in 1987. *SAU
Filep's research mainly dealt with two topics: fuzzy algebra and the history of mathematics. He was the one who revealed the efforts of Texas professor GB Halsted in spreading Bolyai 's non-Euclidean geometry to the smallest detail . He conducted research on the topic of fuzzy algebra together with Gyula I. Maurer , and their results were regularly published in several scientific journals. *Wik
1788 Nicole-Reine Lepaute (5 Jan 1723 in Paris, France - 6 Dec 1788 in Saint-Cloud, France) was a French noblewoman who helped Lalande with astronomical calculations. In June 1757 Lalande decided that he would like to attempt to calculate a precise date for the return of Halley's comet. It was known to have been seen in 1305, 1380, 1456, 1531, 1607 and 1682 and Halley, taking into account perturbations to the orbit caused by the gravitational effects of Jupiter, had predicted that the comet would return reaching perihelion in December 1758. However the only way to get a more accurate prediction of its date of return was to calculate the perturbations to the orbit caused by the gravitational effects of both Jupiter and Saturn. Lalande approached Alexis Clairaut for help and Clairaut provided a basic programme of work requiring an extraordinary amount of computation. Lalande then asked Nicole-Reine Lepaute to assist him in the computations. Lalande wrote, "During six months we calculated from morning to night, sometimes even at meals. ... The assistance of Mme Lepaute was such that, without her I should never have been able to undertake the enormous labour, in which it was necessary to calculate the distance of each of the two planets Jupiter and Saturn from the comet, separately for each successive degree for 150 years. *SAU
1893 Rudolf Wolf (7 Jul 1816, 6 Dec 1893) Swiss astronomer and astronomical historian. Wolf's main contribution was the discovery of the 11 year sunspot cycle and he was the codiscoverer of its connection with geomagnetic activity on Earth. In 1849 he devised a system now known as Wolf's sunspot numbers. This system is still in use for studying solar activity by counting sunspots and sunspot groups. In mathematics, Wolf wrote on prime number theory and geometry, then later on probability and statistics - a long paper discussed Buffon's needle experiment. He estimated by Monte Carlo methods.*TIS
).jpg)
1959 Erhard Schmidt (13 Jan 1876 in Dorpat, Estonia (Russian Empire) (now Tartu, Estonia)- 16 Dec 1959 in Berlin, Germany) 1876 Erhard Schmidt (13 January 1876 – 6 December 1959) was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia (now Estonia). His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905. His doctoral dissertation was entitled Entwickelung willkürlicher Funktionen nach Systemen vorgeschriebener and was a work on integral equations.
Together with David Hilbert he made important contributions to functional analysis. He is best known for the Gram-Schmidt orthogonalisation process, which constructs an orthogonal base from any vector space. *Wik
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other.
The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt.
1973 Joseph Leonard Walsh, (September 21, 1895 – December 6, 1973) was an American mathematician. His work was mainly in the field of analysis.
For most of his professional career he studied and worked at Harvard University.*Wik
1990 Lev Arkad'evich Kaluznin (31 Jan 1914 in Moscow, Russia - 6 Dec 1990 in Moscow, Russia) Kaluznin is best known for his work in group theory and in particular permutation groups. He studied the Sylow p-subgroups of symmetric groups and their generalisations. In the case of symmetric groups of degree pn, these subgroups were constructed from cyclic groups of order p by taking their wreath product. His work allowed computations in groups to be replaced by computations in certain polynomial algebras over the field of p elements. Despite the fact that the earliest applications of wreath products of permutation groups was due to C Jordan, W Specht and G Polya, it was Kaluznin who first developed special computational tools for this purpose. Using his techniques, he was able to describe the characteristic subgroups of the Sylow p-subgroups, their derived series, their upper and lower central series, and more. These results have been included in many textbooks on group theory. *SAU
1993 Wolfgang Paul (10 Aug 1913, 6 Dec 1993) German physicist who developed the Paul trap, an electromagnetic device that captures ions and holds them long enough for study and precise measurement of their properties. During the 1950s he developed the so-called Paul trap as a means of confining and studying electrons. The device consists of three electrodes - two end caps and an encircling ring. The ring is connected to an oscillating potential. The direction of the electric field alternates; for half the time the electron is pushed from the caps to the ring and for the other half it is pulled from the ring and pushed towards the caps. For his work he shared the 1989 Nobel Prize for Physics with Hans G. Dehmelt and Norman F. Ramsey.*TIS
1996 Stefan Schwarz (18 May 1914 in Nové Mesto nad Váhom, Austria-Hungarian Empire (now Slovakia) - 6 Dec 1996 in Bratislava, Slovak Republic) In addition to his work on semigroups, number theory and finite fields, Schwarz contributed to the theory of non-negative and Boolean matrices.
Schwarz organized the first International Conference on Semigroups in 1968. At this conference setting up the journal Semigroup Forum was discussed and Schwarz became an editor from Volume 1 which appeared in 1970, continuing as editor until 1982. This was not his first editorial role since he had been an editor of the Czechoslovak Mathematical Journal from 1945 and continued to edit this journal until he was nearly 80 years old. He also founded the Mathematico-Physical Journal of the Slovak Academy of Sciences in 1950 and continued as an editor of the mathematics part of the journal when it split from the physics part to become Mathematica Slovaca until 1990. *SAU
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
No comments:
Post a Comment