Solving Geometric Problem with Pure Logic

I recently came across one of those geometry puzzles with multiple choice answers people like to post.

It struck me that a clever student could figure out the answer without calculations.  Before I go on I'll post the puzzle and let you play at it, but no calculating.  

You see these things all over the place if you are on the internet much.  This one at least was more straightforward than the "95% of people can't do this arithmetic problem" and the do something with order of operations using an obelus  (the spit symbol, ÷, used only in English speaking countries for division, strangely first used in a German book, Teutsche Algebra by Johann Rahn.)  

Anyway, that diversion was to take up a little space between the problem and the answer.

Since I knew the answer I read some of the different approaches in the comments. My favorite was a guy whose solution was pure logic.  

Answers a) and c) rule each other out,  since sides b and  a are the legs of the right triangle, if you switched their names, you get a different radius for congruent right triangles.  Answer b)  can't be right either.  The incircle can not be longer than the hypotenuse, because it is inside the triangle, but in any triangle, the two shorter sides are more than the longest side, which means that the b) answer woud be greater than the hypotenuse.  

So if any of them are true, d) must be the one.  

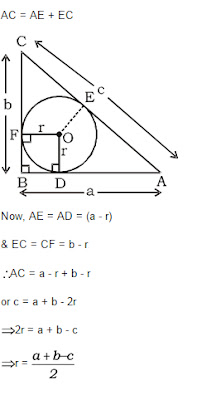
And it is true, but I'm too lazy to write it out, here is a  solution I plucked from  Quora.  

That's the kind of clever thinking that makes teachers smile.