Just browsing through an old Recreations in Mathematics by Dr H. E. Licks (not real name, see below) and discovered something I had wondered about, but never seen, an example of fractions of a unit in Roman engineering. And if you think regular Roman numerals are complex to deal with, check these fractions.
I knew they had symbols of some measures that were themselves fractions, ounces (uncia-12th), inches (uncia), and digits (digitus), for example. You've probably heard of the first two, but digits seems less well known.
But if you had to guess, you'd probably guess finger, and be right. The Romans, like many of us today used 12 inches in a foot (pes), but they also adopted a Greek fraction of 1/16th of a foot, called digitus. While reading the previously mentioned book, I found a whole new set of symbols to represent fractional parts of these named units attributed to Frontinus, a 97 AD Water Commissioner about water flow in roman pipes (fistula) .
Pipes, it seems, were expressed by their diameter in digits, divided into 12th parts of a digit. The symbol - was for a twelfth part of a digit, two of them, = would be 2/12, adding more beside these , == could be four-twelfths. He represented The half unit was represented by an S , 6/12, and more bars added to make 7 through 11 twelfths. Another symbol was introduced for the 24th part of a digit, which looked greatly like the Pound Sterling symbol, for which I substitute L. There was even another for the 288th (a twelfth of a twenty-fourth) part of a digit (that's 1/128th of 1/16 of an inch, a little less than .0005 ". This symbol was represented by something resembling the reverse of a Euro symbol, or the Latin Capital open O, Ɔ, with a little extra line in the back.
The standard flow measure, a quinaria, was the amount from a 1 1/4 digit pipe, (or I =-) . His example of something called a fifty pipe has (diametri digitos) diameter of 7 digits + 1/2 + 5/12 +1/24 + 5/228, which his symbols would write as VII S ==- L ƆV . The V after the 288ths to mean five of them makes you wonder why he would not have done that with the twelfths.
Dr Licks writes, "Perhaps the awkward notation retarded the development of mathematics among the Romans."
Frontinus' document was translated by Clemens Herschel in 1889 from whence Dr Licks wrote Lies, Damned Lies, and Something About Statistics in the early part of his book.
Regular readers of my blog have met the Dr H E Licks annually in earl February in the Events portion:
1880 On 10 February 1880, an article ran in the Daily Times (of Bethlehem, Pennsylvania) describing a remarkable invention recently demonstrated by a local inventor, Dr. H.E. Licks. The invention allowed images to be transmitted by telegraph. In other words, it resembled what people today would recognize as a television. However, Licks called his invention a "diaphote," from the Greek dia meaning "through" and photos meaning "light".
Despite the excitement it generated, the diaphote turned out to be a hoax. However, it wasn't until 1917 that "Dr. H.E. Licks" revealed the hoax in a book, Recreations in Mathematics. Licks himself is believed to have been the pseudonym of Mansfield Merriman (1848-1925), a professor of engineering at Lehigh University. *Museum of Hoaxes
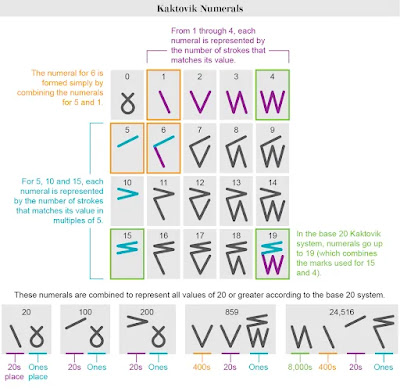
A few years after writing this, I found a story in SciAm about an Inuit tribe that developed a numeral system very similar to tally marks.
When I included them in an article on the history of Tally marks I realized that writing them for division gave an easy way to express them as fractions.
-------original
It was a story in Scientific American, and the original goes deeper than I can, but I want to touch on this new tally based method of numeration with a base twenty syatem broken into base five units that was created working with inuit Children. Their word for five is the word for arm, taliq, and the word for twenty represents the whole person, Iñuiññaq.
Look at the example with 14/2. taking off half the fives, and half the four marks for the W leaves one five and V for two more, the symbol for seven. Turn it over and 2/14 would only require keeping a one above the bar. For all their advances in engineering and such, I wonder if they just didn't think mathematically.

No comments:
Post a Comment