 |
| Zentangle *Jeannie |
Every student who enters upon a scientific pursuit, especially if at a somewhat advanced period of life, will find not only that he has much to learn, but much also to unlearn.
The 66th day of the year; there are 66 different 8-polyiamonds (A generalization of the polyominoes using a collection of equal-sized equilateral triangles (instead of squares) arranged with coincident sides.)
Route 66, known as the Main Street of America was dubbed the "Mother Road" by novelist John Steinbeck,
The sum of the divisors of 3, 1+3 =4=2^2
The sum of the divisors of 22, 1+2+11+22=36 = 6^2
The next number with this quality is 3 x 22=66, whose divisors add to 4*36 = 144 = (12)^2 (alas, beyond that things go wacky!) divisors of 70 are same as 66)
If you wrote out all the numbers on a 12 hour clock, (HrMin, so 6:03 would be 603, etc.), there would be 66 of them that are prime.
66 is the largest day number of the year which does not have a letter "e" in its English spelling. Sixty-six is the 19th such numbers in the year, but the next number without an "e" is 2000.
Sixty Six is an unincorporated community in Orangeburg County, South Carolina, United States. Sixty Six is located along U.S. Route 21, north of Branchville.
1750 Two days after delivering his paper on precession, Recherches sur la Précession, to the Berlin Academy, Euler writes to credit d'Alembert for a paper which inspired him to return to the topic after previously giving up.
I applied myself repeatedly and for a long time to the problem of precession, but I always encountered an obstacle − the great number of circumstances that have to be taken into account, and above all this problem: given a body turning about any axis freely, and acted upon by an oblique force, to find the change caused both in the axis of rotation and in the motion. The solution of this is absolutely required for the subject you have so happily developed. But with respect to this problem all my investigations had been unavailing so far, and I would not have applied myself to it further, if I had not seen that the solution must necessarily be encompassed in your treatise, although I was not able to find it there, which at first increased so much the more my desire to develop your whole method. But I must also confess that I could not follow you in the preliminary propositions you employed, for your way of carrying out the calculation was not yet very familiar to me… . But now that I have succeeded better in the investigation of this same subject, having been assisted by some insights in your work by which I was little by little enlightened, I have come to be able to judge your excellent conclusions.*Curtis Wilson, Historia Mathematica, Volume 35, Issue 4, November 2008, Pages 329–332
1785 James Hutton, geologist, presents his full theory of uniformitarianism at a meeting of the Royal Society of Edinburgh. He is credited with Establishing geology as a true science, formulating his controversial 'Theory of the Earth', and being the first person to suggest that the Earth is millions of years old.
His 'Theory of the Earth' noted that features of the Earth’s surface must have formed through cycles of natural processes over geologic time (ie rocks on mountains may have been formed in the bottom of the sea). His geological research contributed to the underlying principles of uniformitarianism.
In 1799, the Royal Institution in England was founded at a meeting at the Soho Square house of the President of the Royal Society, Joseph Banks (1743-1820). A list was read of the names of fifty-eight gentlemen who had agreed to contribute fifty guineas each to be a Proprietor of a new Institution for diffusing the knowledge, and facilitating the general introduction, of useful mechanical inventions and improvements; and for teaching, by courses of philosophical lectures and experiments, the application of science to the common purposes of life. A group of Proprietors met to discuss the Proposals for such an Institution put together in the previous weeks by Sir Benjamin Thompson Rumford. *TIS The Royal Institution is the oldest independent research body in the world. *RI
1825 The University of Virginia's first classes met on March 7, 1825. Other universities of the day allowed only three choices of specialization: Medicine, Law, and Religion. Under Jefferson's guidance, the University of Virginia became the first in the United States to allow specializations in such diverse fields as Astronomy, Architecture, Botany, Philosophy, and Political Science. Jefferson explained, "This institution will be based on the illimitable freedom of the human mind. For here we are not afraid to follow truth wherever it may lead, nor to tolerate any error so long as reason is left free to combat it."
The year before, in the presence of James Madison, the Marquis de Lafayette toasted Jefferson as "father" of the University of Virginia at the school's inaugural banquet *Wik
1876 Alexander Graham Bell receives a patent for the telephone in the US. Below is the drawing accompanying his patent application.
1907 Nature Magazine carried an article from Francis Galton entitled Vox Populi, regarding what is now called "crowd wisdom." In a rural fair in Plymouth England, there had occurred a spectacle in which the locals could guess the dressed weight of an Oxen to be slaughtered. Tickets cost six pence, but the grand prize was the butchered carcass of the animal, and there seems to have been several smaller prizes. Galton arranged to acquire the cards after the vote. The 787 guesses ranged from around 1000 pounds to about 1500. The median Guess was 1207 pounds.... and when they weighed the beast, "and the weight of the dressed ox proved to be 1198 lb.; so the vox populi was in this case 9 lb., or 0.8 per cent of the whole weight too high." You can almost here the surprise in Galton, who was not, as my grandson would say, "a fan" of the common man. *wisdomofcrowds.blogspot
1912 Roald Amundsen announces his discovery of the South Pole (located 14 December 1911).the Norwegian Antarctic expedition of 1910–12 which was the first to reach the South Pole, famously beating Robert Scott's expedition by 33-34 days.
Amundsen is recognized as the first person to have reached both poles. He is also known as having the first expedition to traverse the Artic's Northwest Passage (1903–06).*On This Day
Norway Flag at the South Pole:
1918 Jan Lukasiewicz in his “Farewell Lecture” as Rector of Warsaw University announces the work on three-valued logic which he had worked out the summer before. [Selected Works, 84–86.] His parenthesis-free notation was discovered in 1924 and first used in print in 1929 . Today this “Reverse Polish Notation” is widely used. See Hewlett-Packard Personal Computer Digest, vol.7 (1980). *VFR
1929 In 1928,Alexander Fleming discovered the green mould he was working with produced a substance that could kill many common bacteria that infect humans. He called this new, exciting substance "mould juice".
It took him a couple of months to come up with a better name and on 7 March 1929, he named it penicillin. *The Nobel Prize

In 1935, Monopoly was first marketed by Charles Darrow, with the symbol of Rich Uncle Pennybags. He had invented the game on 7 Mar 1933. (See Note Below) A patent was issued for the game 31 Dec 1935, assigned to Parker Brothers, Inc.(No. 2,026,082). The patent described a "Board Game Apparatus... intended primarily to provide a game of barter, thus involving trading and bargaining" in which "much of the interest in the game lies in trading and in striking shrewd bargains." Illustrations showed the playing board, pieces, 22 "Title cards of the respective Real Estate holdings," Utilities, Chance and Community Chest cards, and scrip money. On the throw of the dice, the players may move onto Real Estate locations which may be acquired.*TIS
The history of the board game Monopoly can be traced back to the early 20th century. The earliest known design was by the American Elizabeth Magie created in 1903. A series of board games was developed from 1906 through the 1930s that involved the buying and selling of land and the development of that land. By 1934, a board game had been created much like the version of Monopoly sold by Parker Brothers and its parent companies through the rest of the 20th century, and into the 21st. Several people, mostly in the Midwestern United States and near the East Coast, contributed to the game's design and evolution.
By the 1970s, the idea that the game had been created solely by Charles Darrow had become popular folklore: it was printed in the game's instructions and even in the 1974 book The Monopoly Book: Strategy and Tactics of the World's Most Popular Game by Maxine Brady.*Wik
1929 The previously known "mold juice" was renamed. "Alexander Fleming discovered the green mold he was working with produced a substance that could kill many common bacteria that infect humans. He called this new, exciting substance "mould juice". Only after a couple of months, on 7 March 1929, did he name it penicillin." * @NobelPrize
1946 Bikini Atoll islanders are evacuated by the US government to make way for a nuclear testing site. *On This Day
1957 Teenager John H Conway in his first year at Cambridge writes to H S M Coxeter to ask a question about the {5,3,3} Polytope in four-dimensions. In the five page letter Conway tells the Professor that "Over the past year my copy of your edition of Ball's 'Mathematical Recreations' has accumulated an astonishing number of notes and some corrections... but one or two may seem important." *Siobhan Roberts, King of Infinite Space
1962 Ground-breaking report "Smoking and Health" published by the British Royal College of Physicians, first major report to warn of the dangers of smoking. *On This Day
1973 Comet Kohoutek, formally designated C/1973 E1, 1973 XII, and 1973f, was first sighted on March 7, 1973 by Czech astronomer Luboš Kohoutek.( M. J. Hendrie, gives the "discovery" as March 18, while observing plates taken on March 7th and 9th. *Journal of the British Astronomical Association, vol.110, no.1, p.9-19) It attained perihelion on 28 December that same year. *Wik
Image is photograph from the Joint Observatory for Cometary Research, South Baldy Mountain, New Mexico, on December 7, 1973, about 3 weeks before perihelion.
In 1979, scientists discovered a ring around Jupiter while examining photographs taken by the Voyager 1 spacecraft. The rings of Saturn had been known since 1610. Astronomers had recognized rings around Uranus in 1977. *TIS
1989 In a review of Profscam: Professors and the Demise of Higher Education by Charles J. Sykes in The Los Angeles Times, the reviewer wrote that this is how Sykes would word an advertisement at a big research university: “WANTED: University professor. Good salary. Little work. Lots of prestige. Possible lifetime security. Not much contact with students. Plenty of time to research your obscure interests. Good chance for government grants and corporate consulting.” *VFR
1996 1st surface photos of Pluto (photographed by Hubble Space Telescope). The image below shows comparison of first photos, and those almost two decades later.
BIRTHS
1792 (1st Baronet) Sir John (Frederick William) Herschel (7 Mar 1792; 11 May 1871 at age 79) was an English astronomer. As successor to his father, Sir William Herschel, he discovered another 525 nebulae and clusters. John Herschel was a pioneer in celestial photography, and as a chemist contributed to the development of sensitized photographic paper (independently of Talbot). In 1819, he discovered that sodium thiosulphate dissolved silver salts, as used in developing photographs. He introduced the terms positive image and negative image. Being diverse in his research, he also studied physical and geometrical optics, birefringence of crystals, spectrum analysis, and the interference of light and sound waves. To compare the brightness of stars, he invented the astrometer. *TIS [He was buried in Westminster Abbey.]
1824 Delfino Codazzi (7 March 1824 in Lodi, Italy
Died: 21 July 1873 in Pavia, Italy) was an Italian mathematician who worked in differential geometry.*SAU
1837 Henry Draper (7 Mar 1837, 20 Nov 1882) American physician and amateur astronomer who made the first photograph of the spectrum of a star (Vega), in 1872. He was also the first to photograph a nebula, the Orion Nebula, in 1880. For his photography of the transit of Venus in 1874, Congress ordered a gold medal struck in his honour. His father, John William Draper, in 1840 had made the first photograph of the Moon.*TIS
 |
| Two photographs of the Great Nebula in Orion, by Henry Draper, 1880 (left), and 1882 (right) *LindaHallOrg |
1870 Ernst Leonard Lindelöf, (7 March 1870, Helsinki (in Swedish: Helsingfors)–4 June 1946, Helsinki) was a Finnish topologist after whom Lindelöf spaces are named; he was the son of Leonard Lorenz Lindelöf and brother of the philologist Uno Lorenz Lindelöf.
Lindelöf studied at the University of Helsinki, where he completed his Ph.D. in 1893, became a docent in 1895 and professor of Mathematics in 1903. He was a member of the Finnish Society of Sciences and Letters.
In addition to working on mathematical topics as diverse as differential equations and the gamma function, Lindelöf actively promoted the study of the history of Finnish mathematics.*Wik
1886 Sir Geoffrey Ingram Taylor OM (7 March 1886 – 27 June 1975) was a British physicist, mathematician and expert on fluid dynamics and wave theory. His biographer and one-time student, George Batchelor, described him as "one of the most notable scientists of this (the 20th) century". His final research paper was published in 1969, when he was 83. In it he resumed his interest in electrical activity in thunderstorms, as jets of conducting liquid motivated by electrical fields. The cone from which such jets are observed is called the Taylor cone for his namesake. In the same year Taylor was appointed to the Order of Merit. He suffered a stroke in 1972 which effectively put an end to his work; he died in Cambridge in 1975.*Wik Tayler was the grandson of George Boole, and is responsible for introducing Donald Coxeter to Alicia Boole Stott. Here is more on "Those Amazing Boole Girls", and their successors.
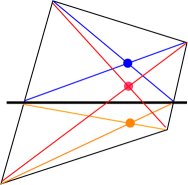
1893 Anna Margaret Mullikin (March 7, 1893 - August 24, 1975) She was born in Baltimore, Maryland and attended Goucher College, which was then a women's college located in the same city. While there she managed her class basketball team, participated on the swimming team, and earned her A.B. degree in 1915. That same year her name was mentioned in the American Mathematical Monthly [Vol. 22, No. 5 (May 1915),pp. 165-166] for solving the following geometry problem:
A quadrilateral of any shape whatever is divided by a transversal into two quadrilaterals. The diagonals of the original figure and those of the two resulting (smaller) figures are then drawn. Show that their three points of intersection are collinear.In 1918 she entered the graduate program in mathematics at the University of Pennsylvania, earning her master's degree in 1919. She continued her graduate studies at Penn during the 1919-1920 academic year under the direction of the topologist, Robert L. Moore, while also teaching at the Stevens School in Germantown, Pennsylvania, another private preparatory school for girls. In the fall of 1920 she moved to the University of Texas along with Moore, who had convinced the Texas math department to appoint her as an instructor. Mullikin stayed in Texas for only the one academic year before returning to Philadelphia to complete the requirements for her degree from the University of Pennsylvania, with Moore still as her advisor. She received her Ph.D. in mathematics in 1922. Mullikin did not pursue mathematical research after earning her Ph.D. She spent the rest of her professional career as a high school mathematics teacher, first at William Penn High School for Girls in Philadelphia for one year, and then at Germantown High School where she remained until her retirement in 1959. She was appointed head of the mathematics department in 1952. In 1956 she was a joint author with Ethel and Ewart Grove for the textbook Algebra and Its Use. *Agnes Scott College
The published solution was by Vola Barton, also from Goucher College, with the remark "Also solved by Anna Mullikin."
1900 Fritz Wolfgang London (7 Mar 1900; 30 Mar 1954 at age 53) German-American physicist who, with Walter Heitler, devised the first quantum mechanical treatment of the hydrogen molecule, while working with Erwin Schrödinger at the University of Zurich. In a seminal paper (1927), they developed a wave equation for the hydrogen molecule with which it was possible to calculate approximate values of the molecule's ionization potential, heat of dissociation, and other constants. These predicted values were reasonably consistent with empirical values obtained by spectroscopic and chemical means. This theory of the chemical binding of homopolar molecules is considered one of the most important advances in modern chemistry. The approach is later called the valence-bond theory. *TIS
1905 John Macnaghten Whittaker I(7 March 1905 in Cambridge, England - 29 Jan 1984 in Sheffield, England) was the son of Edmund Whittaker. He studied at Edinburgh University and Cambridge. After posts at Edinburgh and Cambridge he became Professor at Liverpool though his tenure was interrupted by service in World War II. He left Liverpool to become Vice-Chancellor of Sheffield University. He worked in Quantum Mechanics and Complex Analysis. *SAU
1922 Olga Aleksandrovna Ladyzhenskaya (March 7, 1922, Kologriv – January 12, 2004, St. Petersburg) was a Soviet and Russian mathematician. She was known for her work on partial differential equations (especially Hilbert's 19th problem) and fluid dynamics. She provided the first rigorous proofs of the convergence of a finite difference method for the Navier-Stokes equations. She was a student of Ivan Petrovsky. She was awarded the Lomonosov Gold Medal in 2002.*Wik
Allan Hale (born 1958) American astronomer and writer who independently co-discovered (with Thomas Bopp) the unusually bright Comet Hale-Bopp (23 Jul 1995), the farthest comet ever to be discovered by amateurs. After service in the navy, he worked at the Jet Propulsion Laboratory (1983-86) as an engineering contractor on several projects, including Voyager II. After earning a Ph.D. in astronomy, he founded the Southwest Institute for Space Research (now named the Earthrise Institute). His interests include near-Earth objects and their possible impact on Earth, and the search for planets outside our solar system. Hale advocates for improved science literacy in society; for better career opportunities for graduating scientists; and develops international collaboration for observation projects.
Hale-Bop Art bu Daniel Durda, my former student and accomplished Astronomer himself.(These rwo things may not be directly related)
DEATHS
1809 Jean-Pierre Blanchard (4 July 1753 – 7 March 1809) , a French balloonist, was born July 4, 1753. The Golden Age of Ballooning began on Nov. 21, 1783, when Pilâtre de Rozier and François d'Arlandes soared aloft in a hot-air balloon made by the Montgolfier brothers. They launched from the Château de la Muette just outside Paris and floated for some 5 miles. Just over a week later, Jacques-Alexandre Charles and Nicolas Robert ascended to 3000 feet from the Tuileries in Paris, this time in a hydrogen balloon. Blanchard was caught up immediately in balloon frenzy, designed his own hydrogen balloon, complete with "oars" to swim through the air and an always-open parachute to slow descent should the gas bag spring a leak, and headed for the skies . He made his first ascent in a hydrogen balloon on Mar. 2, 1784, lifting off from the Champ de Mars. If there is a surviving contemporary image of that ascent, I have not seen it.
The difference between Blanchard and the Montgolfier brothers and Jacques Charles is that Blanchard was in it for the money. He was the first barnstorming balloonist who charged admission for his ascents and seems to have given the public (who showed up by the thousands) their money's worth, especially on the first ascent, when a military student demanded to come along and attacked Blanchard and the balloon with a sword when he was refused. The somewhat bloodied Blanchard proceeded with the flight anyway, which I am sure delighted the crowd.
Seeking larger paydays, Blanchard travelled with his balloon to England in August of 1784 and began to organize public ascents there. He made one ascent from Chelsea, for which (so it is recorded) 400,000 people showed up. He made the ascent with an English physician, who was added to the gondola to increase local interest. An engraving recorded the event, which took place on Oct. 16, 1784. Blanchard then ascended with another physician, John Jeffries (an ex-American, actually), on Nov. 30, 1784, and this time they wafted all the way from London to Kent.
This set the stage for Blanchard's goal all along, to balloon across the English Channel. Pilâtre de Rozier had the same idea; he was sitting on the other side of the channel with his hydrogen balloon, waiting for favorable winds to take him westward to Dover. Blanchard won the battle of the winds. He and Jeffries took off from Dover on Jan. 7, 1785 (fourth image). They almost ended up in the sea, as their bag of hydrogen was providing insufficient lift, and they threw nearly everything overboard, including most of their clothes, to maintain altitude. But the balloon for some reason recovered its buoyancy, and they made it to Calais and beyond, landing at Guines, to the great excitement of the local populace.
1889 Angelo Genocchi (5 March 1817 – 7 March 1889) was an Italian mathematician who specialized in number theory. He worked with Giuseppe Peano. The Genocchi numbers are named after him. G(t)= 2t/(et+1)for integer values of t. The first few are 1, −1, 0, 1, 0, −3, 0, 17...(A001469 in OEIS)
Genocchi was President of the Academy of Sciences of Turin.*Wik The unsigned coefficients of Genocchi numbers give expansion of x*tan(x/2). *PB
1922 Axel Thue(19 Feb 1863 in Tönsberg, Norway - 7 March 1922 in Oslo, Norway) Thue studied Diophantine equations, showing that, for example, y3 - 2x2 = 1 cannot be satisfied by infinitely many pairs of integers. Edmund Landau, in 1922, described Thue's work as, ".. the most important discovery in elementary number theory that I know. "
Thue's Theorem states, " If f (x, y) is a homogeneous polynomial with integer coefficients, irreducible in the rationals and of degree > 2 and c is a non-zero integer then f (x, y) = c has only a finite number of integer solutions." *SAU
1964 Samuel Stanley Wilks (June 17, 1906 – March 7, 1964) was an American mathematician and academic who played an important role in the development of mathematical statistics, especially in regard to practical applications.
Born in Little Elm, Texas (Little Elm was once a quiet farm town, and today is one of the fastest growing municipalities in Texas) and raised on a farm, Wilks was educated at the University of Iowa, where he acquired his Ph.D. under Everett F. Linquist; his thesis dealt with a problem of statistical measurement in education, and was published in the Journal of Educational Psychology. Wilks became an instructor in mathematics at Princeton University in 1933; in 1938 he assumed the editorship of the journal Annals of Mathematical Statistics in place of Harry C. Carver. Wilks assembled an advisory board for the journal that included major figures in statistics and probability, among them Ronald Fisher, Jerzy Neyman, and Egon Pearson.
Wilks was named professor of mathematics and director of the Section of Mathematical Statistics at Princeton in 1944, and became chairman of the Division of Mathematics at the University in 1958. He was noted for his work on multivariate statistics and unit-weighted regression.
From the start of his career, Wilks favored a strong focus on practical applications for the increasingly abstract field of mathematical statistics; he also influenced other researchers, notably John Tukey, in a similar direction. Drawing upon the background of his thesis, Wilks worked with the Educational Testing Service in developing the standardized tests like the SAT that have had a profound effect on American education. He also worked with Walter Shewhart on statistical applications in quality control in manufacturing.
During World War II he was a consultant with the Office of Naval Research. Both during and after the War he had a profound impact on the application of statistical methods to all aspects of military planning.
The American Statistical Association named its Wilks Memorial Award in his honor.
Wilks' lambda distribution is a probability distribution related to two independent Wishart distributed variables. It is important in multivariate statistics and likelihood-ratio tests. *Wik
1966 Georg Faber (5 April 1877 in Kaiserslautern, Germany - 7 March 1966 in Munich, Germany) Faber's most important work was on the polynomial expansion of functions. This is the problem of expanding an analytical function in an area bounded by a smooth curve as a sum of polynomials, where the polynomials are determined by the area. These polynomials are now known as 'Faber polynomials' and first appear in Faber's 1903 paper Über polynomische Entwickelungen published in Mathematische Annalen. Another important paper which he also published in Mathematische Annalen, this time in 1909, was Über stetige Funktionen. In this paper he introduced the 'hierarchical basis' and explicitly used it for the representation of functions. In fact Faber was building on the idea of Archimedes who computed approximately using a hierarchy of polygonal approximations of a circle. Only in the 1980s was Faber's idea seen to be an important ingredient for the efficient solution of partial differential equations. One further achievement of Faber is worthy of mention. In 1894 Lord Rayleigh made the following claim:" ... given a fixed area of ox-hide to make a drum, the ground tone is lowest if you make your drum circular. " Two mathematicians independently verified Rayleigh's conjecture, Faber and Edgar Krahn. *SAU
1997 E.M. Purcell (30 Aug 1912; 7 Mar 1997) American physicist who shared, with Felix Bloch of the United States, the Nobel Prize for Physics in 1952 for his independent discovery (1946) of nuclear magnetic resonance in liquids and in solids. Nuclear magnetic resonance (NMR) has become widely used to study the molecular structure of pure materials and the composition of mixtures. The method detects and measures the magnetic fields of atomic nuclei. *TIS
2008 David Gale (December 13, 1921 – March 7, 2008) was a distinguished American mathematician and economist. He was a Professor Emeritus at University of California, Berkeley, affiliated with departments of Mathematics, Economics, and Industrial Engineering and Operations Research. He has contributed to the fields of mathematical economics, game theory, and convex analysis.*Wik
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell



























No comments:
Post a Comment