Things You May Not Know About Four

  Four

The English number four comes to us from the Gothic fidwor which is probably from the same proto root that gave the Latin quattuor. The Greek root for four which still shows up in many mathematical names is tetra. The Pythagoreans had a prayer addressed to four, or at least to fourfoldness, "O holy, holy tetraktys.." which was thought to represent the four elelments: fire, water, air, and earth.

Bill Bryson, in Mother Tounge (pgs 113,114) explains the loss of the "u" in forty. Why is there no "u" in forty?
Four, fourteen, and fourth all have it. So did fourty in the writings of Chaucer. In fact, until the 17th Century when, as Bryson says, "But then, as if by universal decree, it just quietly vanished. No one seems to have remarked on it at the time."

The way four was written has changed over time more than many numbers. Wikipedia's page on the number four shows the following progression for the development of our current 4.

Karl Menninger in Number Words and Number Symbols points out that several of the shapes were used at the same time, and gives a photo (Fig. 260) from the Bamberger Rechembuch of 1483 in which two of the forms are used in the same example of a multiplication problem. He also has this graphic showing three different variants of a four in succesive years by Durer.

The Wikipedia page also gives several interesting tidbits about the uniqueness of four. Among them are the following; "Four is the only English number that, when spelled out, has the number of letters that it names", "Four is the first positive non-Fibonacci number", and "Each natural number divisible by 4 is a difference of squares of two natural numbers, i.e. 4x = y^2 - z^2. Four is also the smallest composite number, and a solution to Brocard's Problem (For what values of n is n! + 1 a perfect square) since 4! + 1 = 5^2.

The fact that the word four has as many letters as the number it names was extended by Martin Gardner into an observation about all numbers. Take any number, use the number of letters in the name to get a new number. Repeat with the new number and eventually, it seems (I have not seen a proof, nor have I ever found an exception) you come to four. For example if we start with thirty, it has 6 letters, so we take six, which has 3 letters, so we write three, which has 5 letters, and at last we come to five, which has four letters.

A Hat Tip to DEB JYOTI MITRA who sent..

The product of four successive natural numbers is one less than a perfect square!

n* ( n+1)*( n+2)* ( n+3)= n* {( n^3) +(1+2 +3) * n^2+ ( 1*2 +2*3+3*1)* n+ 1*2*3}

= n^4+ 6* n^3+11*n^2+6*n+1-1= ( n^2 +3*n+1)^2-1;

If n=1 ;

Then 1*2*3*4 4!=5^2-1;

If n=2 Then this product=2*3*4*5=1*2*3*4*5=5!=11^2-1 

Barney Hughes posted a note about the use of four as a base for counting. "Ed's remark about base-four would have me note that several tribes of California Indians, notably those living in and around Ventura, counted by fours. A complete list of their words for the numbers, 1 to 64, is in Old Mission Library-Archives, Santa Barbara, a holograph by an early nineteenth century missionary. (I have seen it.) While I am at it: there were some twenty linguistic families in California and they used 4, 5, 8, 10, and 20 for their bases, all depending on where they lived rather than on the language or dialect they spoke."

I would add that among some North American Indian tribes (Cree, Crow, Micma) the numerals are true verbs instead of adjectives, and as such are conjugated through all the variations of mood, tense, person and number. 

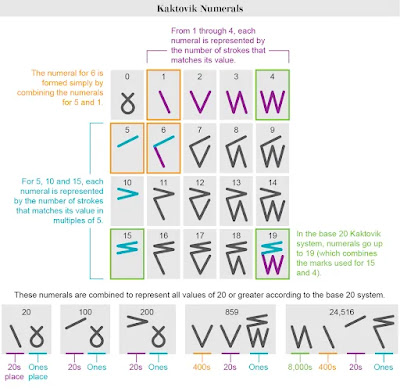
While writing about The History of Tally Sticks, I came across a new system of numbering in base twenty invented recently. In the remote Arctic almost 30 years ago, a group of Inuit middle school students and their teacher invented the Western Hemisphere's first new numeral system in more than a century. The “Kaktovik numerals,” named after the Alaskan village where they were created, looked utterly different from decimal system numerals and functioned differently, too. But they were uniquely suited for quick, visual arithmetic using the traditional Inuit oral counting system, and they swiftly spread throughout the region. Now, with support from Silicon Valley, they will soon be available on smartphones and computers—creating a bridge for the Kaktovik numerals to cross into the digital realm.

I also found that in Bukiyip, a Papua New Guinea language also known as Mountain Arapesh, there are two counting systems, and which one you use depends on what you are counting. Coconuts, days, and fish are counted in base-3. Betel nuts, bananas, and shields are counted in base-4. The word anauwip means 6 in the base-3 system and 24 in the base-4 system! It just depends on whether you are counting cocanuts or bananas......(easy?).

Their word for five is the word for arm, taliq, and the word for twenty represents the whole person, Iñuiññaq.  

The W may differs only a little from the |||| in a regular tally before the slant across it makes a five (arm).

If you study the figures you can see how the zig-zag tallys build up. It's better for representing numbers than the basic tally, because you can represent multiple fives without the tallies for all the ones.