It can be of no practical use to know
that π is irrational,
but if we can know,
it surely would be intolerable not to know.
~ Edward Titchmarsh
The 112th day of the year; 112 is a practical number (aka panarithmetic numbers), any smaller number can be formed with distinct divisors of 112. Student's might explore the patterns of such numbers.
112 is the side of the square that can be tiled with the the fewest
number of distinct integer-sided squares, discovered by A. J. W. Duijvestijn in 1976
112 is the only 3-digit number such that its factorial raised to the sum of its digits and increased by one is prime. I.e., 112!(1+1+2)+1 is prime.
112 = 11 + 13 + 17 + 19 + 23 + 29 (sum of consecutive primes) and
= 1x2 + 2x3 + 3x4 + 4x5 + 5x6 + 6x7 (sum of consecutive oblong or pronic numbers)
112 = 7+9+11+13+15+17 +19+21
Douglas W Boone noted that "_Every_ odd multiple of eight greater than 56 is the sum of eight consecutive positive even numbers. (The smallest sum of eight consecutive positive even numbers is 72 = 2+4+6+8+10+12+14+16.) Allowing zero and negative numbers, every odd multiple of eight, period, is the sum of eight consecutive even numbers. The _even_ multiples of eight (that is, multiples of sixteen) are the sum of eight consecutive _odd_ numbers."
EVENTS
1056, the supernova in the Crab nebula was last seen by the naked eye. The creation of the Crab Nebula corresponds to the bright SN 1054 supernova that was independently recorded by Indian, Arabic, Chinese and Japanese astronomers in 1054 AD. The Crab Nebula itself was first observed in 1731 by John Bevis. The nebula was independently rediscovered in 1758 by Charles Messier as he was observing a bright comet. Messier catalogued it as the first entry in his catalogue of comet-like objects. The Earl of Rosse observed the nebula at Birr Castle in 1848, and referred to the object as the Crab Nebula because a drawing he made of it looked like a crab.*Wik
???? In the century and a half between 1725 and 1875, the French fought and won a certain battle on 22 April of one year, and 4382 days later, also on 22 April, they gained another victory. The sum of the digits of the years is 40. Find the years of the battles. For a solution see Ball’s Mathematical Recreations and Essays, 11th edition, p. 27. *VFR (or see this blog)
1715 (O.S.) A total solar eclipse was observed in England from Cornwall in the south-west to Lincolnshire and Norfolk in the east,the first total solar eclipse visible in London for 500 years. This eclipse is known as Halley's Eclipse, after Edmund Halley (1656–1742) who predicted this eclipse to within 4 minutes accuracy. Halley observed the eclipse from London where the city of London enjoyed 3 minutes 33 seconds of totality. He also drew a predictive map showing the path of totality across England. The original map was about 30 km off the observed eclipse path. After the eclipse, he corrected the eclipse path, and added the path and description of the 1724 total solar eclipse.Note: Great Britain didn't adopt the Gregorian calendar until 1752, so the date was considered 22 April 1715. (Under the modern calendar this would be May 3.) *Wik… The Royal Society reports: Edmund Halley, a Fellow of the Royal Society, is most famous for his work on the orbits of comets, predicting when the one that now bears his name would be seen; however, his interests were more widespread. In 1715 the first total solar eclipse for 500 years took place over England and Wales. Halley, a talented mathematician, realized that such an event would generate a general curiosity and requested that the ‘curious’ across the country should observe ‘what they could’ and make a record of the time and duration of the eclipse. At the time, there were only two universities in England and their astronomy professors did not have much luck in observing the event: ‘the Reverend Mr Cotes at Cambridge had the misfortune to be oppressed by too much company’ and ‘Dr John Keill by reason of clouds, saw nothing distinctly at Oxford but the end’. The event did indeed capture the imagination of the nation and the timings collected allowed Halley to work out the shape of the eclipse shadow and the speed at which it passed over the Earth (29 miles per minute).
1906 First American automobiles meet the first American speed bump. In March of 1906, residents of Chatham Borough, New Jersey had begun construction of a speed control device, crosswalks that were five Inches high, constructed of flagstones and cobblestones. Their creation was a plan to slow down the "very fast pace" (10-15 miles per hour) of the new motor carriages that have begone to take over the roads of the center of town. On "April 22, 1906 with great fanfare and many spectators. Bystanders set up seating and vendors sold hot dogs and pop corn to serve the growing group of onlookers. The next day local newspapers reported on the wreckage and carnage from the newly discovered speed reducers." Here is the article from the New York Times on April 23:
There were several persons in the machine, and when the heavy rubber tires struck the elevation there was a palpitation of the machinery and the car shot up several feet in the air. Goggles, hats, a monkey wrench, sidecombs, hairpins and other articles flew in all directions. The crowd gave a cheer and decided the borough’s plan was effective. The ‘bumps' installed by the borough officials of the village of Chatham to check the speed of automobiles through the village had their first test yesterday, and proved a decided success.
The more conventional speed bumps we are familiar with were not invented until June of 1953. They were created by Nobel Prize winning physicist, Arthur Holly Compton, while he was Chancellor of Washington University in St. Louis, Missouri. *Quora.Com, Wik
1937 "The Law of Anomalous numbers" is read before the American Philosophical Society. This paper described the mathematical idea that is now more commonly called Benford's Law. The paper seems to be available online at the time of this writing.
1939 Frederic Joliot and his group publish their work on the secondary neutrons released in nuclear fission. This was the first demonstration that a chain reaction is indeed possible. Joliot was one of the scientists mentioned in Albert Einstein's letter to President Roosevelt as one of the leading scientists on the course to chain reactions. *Atomic Heritage Foundation
He was a French physicist and husband of Irène Joliot-Curie, with whom he was jointly awarded the Nobel Prize in Chemistry in 1935 ...
1964 The New York Worlds Fair opened in Flushing Meadows, Queens, NY on this day. One technological innovation presented at the fair was the Olivetti Programma 101, one of the first commercial programmable calculators (*The Old Calculator Web Museum "It appears that the Mathatronics Mathatron calculator preceeded [sic] the Programma 101 to market). 40,000 units were sold; 90% of them in the United States where the sale price was $3,200 (increasing to about $3,500 in 1968.)
About 10 Programma 101 were sold to NASA and used to plan the Apollo 11 landing on the Moon.
"By Apollo 11 we had a desktop computer, sort of, kind of, called an Olivetti Programma 101. It was a kind of supercalculator. It was probably a foot and a half square, and about maybe eight inches tall. It would add, subtract, multiply, and divide, but it would remember a sequence of these things, and it would record that sequence on a magnetic card, a magnetic strip that was about a foot long and two inches wide. So you could write a sequence, a programming sequence, and load it in there, and the if you would – the Lunar Module high-gain antenna was not very smart, it didn't know where Earth was. [...] We would have to run four separate programs on this Programma 101 [...]"
— David W. Whittle, 2006
The P101 is mentioned as part of the system used by the US Air Force to compute coordinates for ground-directed bombing of B-52 Stratofortress targets during the Vietnam War. *Wik
In 1970, the first nationwide Earth Day was celebrated in the U.S. as an environmental awareness event celebrated by millions of Americans with marches, educational programs, and rallies. (A local Earth Day celebration had occurred on 21 Mar 1970, in San Francisco, Cal.). Later the same year, President Nixon created the Environmental Protection Agency, or EPA, on 2 Dec 1970 to address America's severe pollution problem. Its mission is to safeguard the nation's water, air and soil from pollution. The agency conducts research, sets standards, monitors activities and helps to enforce environmental protection laws*TIS This stamp was issued in honor of the first celebration of #EarthDay
, which took place in 1970.
2012 A rare daytime meteor was seen and heard streaking over northern Nevada and parts of California on Sunday, just after the peak of an annual meteor shower.
Observers in the Reno-Sparks area of Nevada reported seeing a fireball at about 8 a.m. local time, accompanied or followed by a thunderous clap that experts said could have been a sonic boom from the meteor or the sound of it breaking up high over the Earth. While meteors visible at night typically range in size from a pebble to a grain of sand, a meteor large enough to be seen during daylight hours would presumably be as big as a baseball or softball.*Reuters US
Bill Cooke of the Meteoroid Environments Office at NASA’s Marshall Space Flight Center in Huntsville, Ala., estimates the object was about the size of a minivan, weighed in at around 154,300 pounds (70 metric tons) and at the time of disintegration released energy equivalent to a 5-kiloton explosion. *NASA
Schickard's machine could perform basic arithmetic operations on integer inputs. His letters to Kepler explain the application of his "calculating clock" to the computation of astronomical tables.
In 1935 while researching a book on Kepler, a scholar found a letter from Schickard and a sketch of his calculator, but did not immediately recognize thedesigns or their great importance. Another twenty years passed before the book's editor, Franz Hammer, found additional drawings and instructions for Schickard's second machine and released them to the scientific community in 1955.A professor at Schickard's old university, Tübingen, reconstructed thecalculator based upon Schickard's original plans; it is still on display there today.
He was a friend of Kepler and did copperplate engravings for Kepler's Harmonice Mundi. He built the first calculating machine in 1623, but it was destroyed in a fire in the workshop in 1624.
, which took place in 1970.
2012 A rare daytime meteor was seen and heard streaking over northern Nevada and parts of California on Sunday, just after the peak of an annual meteor shower.
Observers in the Reno-Sparks area of Nevada reported seeing a fireball at about 8 a.m. local time, accompanied or followed by a thunderous clap that experts said could have been a sonic boom from the meteor or the sound of it breaking up high over the Earth. While meteors visible at night typically range in size from a pebble to a grain of sand, a meteor large enough to be seen during daylight hours would presumably be as big as a baseball or softball.*Reuters US
 |
| A meteor in the sky above Reno, Nevada on April 22, 2012. Image credit: Lisa Warren |
Bill Cooke of the Meteoroid Environments Office at NASA’s Marshall Space Flight Center in Huntsville, Ala., estimates the object was about the size of a minivan, weighed in at around 154,300 pounds (70 metric tons) and at the time of disintegration released energy equivalent to a 5-kiloton explosion. *NASA
BIRTHS
1592 Wilhelm Shickard (22 April 1592 – 24 October 1635) He invented and built a working model of the first modern mechanical calculator. *VFR In 1935 while researching a book on Kepler, a scholar found a letter from Schickard and a sketch of his calculator, but did not immediately recognize thedesigns or their great importance. Another twenty years passed before the book's editor, Franz Hammer, found additional drawings and instructions for Schickard's second machine and released them to the scientific community in 1955.A professor at Schickard's old university, Tübingen, reconstructed thecalculator based upon Schickard's original plans; it is still on display there today.
He was a friend of Kepler and did copperplate engravings for Kepler's Harmonice Mundi. He built the first calculating machine in 1623, but it was destroyed in a fire in the workshop in 1624.
Original drawing taken from F. Seck (Editor) 'Wilhelm Schickard 1592–1635, Astronom, Geograph, Orientalist, Erfinder der Rechenmaschine', Tübingen, 1978
1724 Immanuel Kant (22 April 1724 – 12 February 1804) in Konigsberg, Germany. German philosopher, trained as a mathematician and physicist, who published his General History of Nature and theory of the Heavens in 1755. This physical view of the universe contained three anticipations of importance to astronomers. 1) He made the nebula hypothesis ahead of Laplace. 2) He described the Milky Way as a lens-shaped collection of stars that represented only one of many "island universes," later shown by Herschel. 3) He suggested that friction from tides slowed the rotation of the earth, which was confirmed a century later. In 1770 he became a professor of mathematics, but turned to metaphysics and logic in 1797, the field in which he is best known. *TIS
1807 Luigi Palmieri (April 22, 1807 – September 9, 1896) was an Italian physicist and meteorologist. He was famous for his scientific studies of the eruptions of Mount Vesuvius, for his researches on earthquakes and meteorological phenomena and for improving the seismographer of the time. Using a modified Peltier electrometer, he also carried out research in the field of atmospheric electricity. Other scientific contributions included the development of a modified Morse telegraph, and improvements to the anemometer and pluviometer. *Wik
1811 Ludwig Otto Hesse (22 April 1811 in Königsberg, Prussia (now Kaliningrad, Russia)- 4 Aug 1874 in Munich, Germany)Hesse worked on the development of the theory algebraic functions and the theory of invariants. He is remembered particularly for introducing the Hessian (matrix)determinant. *SAU The Hessian matrix is a square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables.*Wik
1816 The French general, Charles Denis Sauter Bourbaki was born. There is a statue of him in Nancy, France, where Jean Dieudonn´e once taught. The polycephalic mathematician Nicolas Bourbaki was named after him. See Joong Fang, Bourbaki, Paideia Press, 1970, p. 24.*VFR
1830 Thomas Archer Hirst FRS (22 April 1830 – 16 February 1892) was a 19th century mathematician, specialising in geometry. He was awarded the Royal Society's Royal Medal in 1883.Hirst was a projective geometer in the style of Poncelet and Steiner. He was not an adherent of the algebraic geometry approach of Cayley and Sylvester, despite being a personal friend of theirs. His specialty was Cremona transformations.*Wik
1884 David Enskog (April 22, 1884, Västra Ämtervik, Sunne – June 1, 1947,Stockholm) was a Swedish mathematical physicist. Enskog helped develop the kinetic theory of gases by extending the Maxwell–Boltzmann equations.*Wik
1887 Harald August Bohr (22 April 1887 – 22 January 1951) was a Danish mathematician and footballer. After receiving his doctorate in 1910, Bohr became an eminent mathematician, founding the field of almost periodic functions. His brother was the Nobel Prize-winning physicist Niels Bohr. He was a member of the Danish national football team for the 1908 Summer Olympics, where he won a silver medal.
A collaboration with Göttingen-based Edmund Landau resulted in the Bohr–Landau theorem, regarding the distribution of zeroes in zeta functions.
Bohr worked in mathematical analysis, founding the field of almost periodic functions, and worked with the Cambridge mathematician G. H. Hardy.
Bohr was also an excellent football player. He had a long playing career with Akademisk Boldklub, making his debut as a 16-year-old in 1903. During the 1905 season he played alongside his brother Niels, who was a goalkeeper. Harald was selected to play for the Danish national team in the 1908 Summer Olympics, where football was an official event for the first time. The opening match of the 1908 Olympic tournament was Denmark's first official international football match. Bohr scored two goals as Denmark beat the French "B" team 9–0. In the next match, the semi-final, Bohr played in a 17–1 win against France, which remains an Olympic record. Denmark faced hosts Great Britain in the final, but lost 2–0, and Bohr won a silver medal. His popularity as a footballer was such that when he defended his doctoral thesis the audience was reported as having more football fans than mathematicians.
Danish football team at the 1908 Olympic games. Bohr is in the top row, 2nd from left.
1891 Sir Harold Jeffreys (22 Apr 1891, 18 Mar 1989 at age 97)English astronomer, geophysicist and mathematician who had diverse scientific interests. In astronomy he proposed models for the structures of the outer planets, and studied the origin of the solar system. He calculated the surface temperatures of gas at less than -100°C, contradicting then accepted views of red-hot temperatures, but Jeffreys was shown to be correct when direct observations were made. In geophysics he researched the circulation of the atmosphere and earthquakes. Analyzing earthquake waves (1926), he became the first to claim that the core of the Earth is molten fluid. Jeffreys also contributed to the general theory of dynamics, aerodynamics, relativity theory and plant ecology.*TIS
1903 Taro Morishima (22 April 1903 in Wakayama, Japan - 8 Aug 1989 in Tokyo, Japan) a Japanese mathematician specializing in algebra who attended University of Tokyo in Japan. Morishima published at least thirteen papers, including his work on Fermat's Last Theorem, and a collected works volume published in 1990 after his death. He also corresponded several times with American mathematician H. S. Vandiver.
Morishima's Theorem on FLT:
Let m be a prime number not exceeding 31. Let p be prime, and let x, y, z be integers such that xp + yp + zp = 0. Assume that p does not divide the product xyz. Then, p2 must divide mp − 1-1. *Wik
1904 J(ulius) Robert Oppenheimer was a U.S. theoretical physicist and science administrator, noted as director of the Los Alamos laboratory during development of the atomic bomb (1943-45) and as director of the Institute for Advanced Study, Princeton (1947-66). Accusations as to his loyalty and reliability as a security risk led to a government hearing that resulted the loss of his security clearance and of his position as adviser to the highest echelons of the U.S. government. The case became a cause célèbre in the world of science because of its implications concerning political and moral issues relating to the role of scientists in government. *TIS
1910 Norman Earl Steenrod (April 22, 1910 – October 14, 1971) was a preeminent mathematician most widely known for his contributions to the field of algebraic topology. He was born in Dayton, Ohio, and educated at Miami University and University of Michigan (A.B. 1932). After receiving a master's degree from Harvard University in 1934, he enrolled at Princeton University. He completed his Ph.D. under the direction of Solomon Lefschetz, with a thesis titled Universal homology groups. He held positions at the University of Chicago from 1939 to 1942, and the University of Michigan from 1942 to 1947. He moved to Princeton University in 1947, and remained on the Faculty there for the rest of his career. He died in Princeton.
Thanks to Lefschetz and others, the cup product structure of cohomology was understood by the early 1940s. Steenrod was able to define operations from one cohomology group to another (the so-called Steenrod squares) that generalized the cup product. The additional structure made cohomology a finer invariant. The Steenrod cohomology operations form a (non-commutative) algebra under composition, known as the Steenrod algebra.
His book The Topology of Fiber Bundles is a standard reference. In collaboration with Samuel Eilenberg, he was a founder of the axiomatic approach to homology theory. *Wik
1929 Sir Michael Francis Atiyah, OM, FRS, FRSE (22 April 1929, 11 January 2019) was a British mathematician working in geometry.
was awarded the Fields Medal in 1966 for his work in developing K-theory, a generalized Lefschetz fixed-point theorem and the Atiyah–Singer theorem, for which he also won the Abel Prize jointly with Isadore Singer in 2004. Atiyah received a knighthood in 1983 and the Order of Merit in 1992. He also served as president of the Royal Society (1990-95). *TIS *Wik
A Möbius band is the simplest non-trivial example of a vector bundle.
1946 Paul Charles William Davies, AM (22 April 1946, ) is an English physicist, writer and broadcaster, currently a professor at Arizona State University as well as the Director of BEYOND: Center for Fundamental Concepts in Science. He has held previous academic appointments at the University of Cambridge, University of London, University of Newcastle upon Tyne, University of Adelaide and Macquarie University. His research interests are in the fields of cosmology, quantum field theory, and astrobiology. He has proposed that a one-way trip to Mars could be a viable option.*Wik
DEATHS
1945 Wilhelm Cauer (June 24, 1900 – April 22, 1945) was a German mathematician and scientist. He is most noted for his work on the analysis and synthesis of electrical filters and his work marked the beginning of the field of network synthesis. Prior to his work, electronic filter design used techniques which accurately predicted filter behaviour only under unrealistic conditions. This required a certain amount of experience on the part of the designer to choose suitable sections to include in the design. Cauer placed the field on a firm mathematical footing, providing tools that could produce exact solutions to a given specification for the design of an electronic filter. *Wik
By the end of World War II, he was, like millions of less-distinguished countrymen and -women, merely a person in the way of a terrible conflagration.
Cauer succeeded in evacuating his family west, where the American and not the Soviet army would overtake it — but for reasons unclear he then returned himself to Berlin. His son Emil remembered the sad result.
The last time I saw my father was two days before the American Forces occupied the small town of Witzenhausen in Hesse, about 30 km from Gottingen. We children were staying there with relatives in order to protect us from air raids. Because rail travel was already impossible, my father was using a bicycle. Military Police was patrolling the streets stopping people and checking their documents. By that time, all men over 16 were forbidden to leave towns without a permit, and on the mere suspicion of being deserters, many were hung summarily in the market places. Given this atmosphere of terror and the terrible outrages which Germans had inflicted on the peoples of the Soviet Union, I passionately tried to persuade my father to hide rather than return to Berlin, since it was understandable that the Red Army would take its revenge. But he decided to go back, perhaps out of solidarity with his colleagues still in Berlin, or just due to his sense of duty, or out of sheer determination to carry out what he had decided to do.*ExecutedToday.com
Seven months after the ending of that war, my mother succeeded in reaching Berlin and found the ruins of our house in a southern suburb of the city. None of the neighbors knew about my father’s fate. But someone gave identification papers to my mother which were found in a garden of the neighborhood. The track led to a mass grave with eight bodies where my mother could identify her husband and another man who used to live in our house. By April 22, 1945, the Red Army had crossed the city limits of Berlin at several points. Although he was a civilian and not a member of the Nazi Party, my father and other civilians were executed by soldiers of the Red Army. The people who witnessed the executions were taken into Soviet captivity, and it was not possible to obtain details of the exact circumstances of my father’s death.
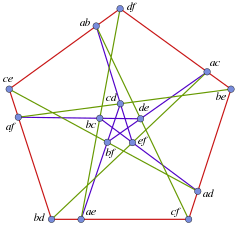1948 Herbert William Richmond (17 July 1863 Tottenham, England – 22 April 1948 Cambridge, England) was a mathematician who studied the Cremona–Richmond configuration. He was elected a Fellow of the Royal Society in 1911. TThe Cremona–Richmond configuration is a configuration of 15 lines and 15 points, having 3 points on each line and 3 lines through each point, and containing no triangles.*Wik
1989 Emilio Gino Segrè (1 Feb 1905; 22 Apr 1989) was an Italian-born American physicist who was co-winner, with Owen Chamberlain of the United States, of the Nobel Prize for Physics in 1959 for the discovery of the antiproton, an antiparticle having the same mass as a proton but opposite in electrical charge. He also created atoms of the man-made new element technetium (1937) and astatine (1940). Technetium occupied a hitherto unfilled space in the body of the Periodic Table, and was the first man-made element not found in nature. Astatine exists naturally only in exceedly small quantities because as a decay product of larger atoms, and having a half-life of only a few days, it quickly disappears by radioactively decay to become atoms of another element.*TIS
 |
| L to R Rasetti, Fermi,Segre. |
2001 John Frank Allen, FRS FRSE (May 5, 1908 – April 22, 2001) was a Canadian-born physicist. codiscovered the superfluidity of liquid helium near absolute zero temperature. Working at the Royal Society Mond Laboratory in Cambridge, with Don Misener he discovered (1930's) that below 2.17 kelvin temperature, liquid helium could flow through very small capillaries with practically zero viscosity. Independently, P. L. Kapitza in Moscow produced similar results at about the same time. Their two articles were published together in the 8 Jan 1938 issue of the journal Nature. Superfluidity is a visible manifestation resulting from the quantum mechanics of Bose- Einstein condensation. By 1945, research in Moscow delved into the microscopic aspect, which Allen did not pursue.*TIS
====================================================
2002 Victor Frederick Weisskopf (September 19, 1908 – April 22, 2002) was an Austrian-born American theoretical physicist. He did postdoctoral work with Werner Heisenberg, Erwin Schrödinger, Wolfgang Pauli and Niels Bohr. During World War II he worked at Los Alamos on the Manhattan Project to develop the atomic bomb, and later campaigned against the proliferation of nuclear weapons.
His brilliance in physics led to work with the great physicists exploring the atom, especially Niels Bohr, who mentored Weisskopf at his institute in Copenhagen. By the late 1930s, he realized that, as a Jew, he needed to get out of Europe. Bohr helped him find a position in the U.S.
In the 1930s and 1940s, 'Viki', as everyone called him, made major contributions to the development of quantum theory, especially in the area of Quantum Electrodynamics.[3] One of his few regrets was that his insecurity about his mathematical abilities may have cost him a Nobel prize when he did not publish results (which turned out to be correct) about what is now known as the Lamb shift. *Wik
His brilliance in physics led to work with the great physicists exploring the atom, especially Niels Bohr, who mentored Weisskopf at his institute in Copenhagen. By the late 1930s, he realized that, as a Jew, he needed to get out of Europe. Bohr helped him find a position in the U.S.
In the 1930s and 1940s, 'Viki', as everyone called him, made major contributions to the development of quantum theory, especially in the area of Quantum Electrodynamics.[3] One of his few regrets was that his insecurity about his mathematical abilities may have cost him a Nobel prize when he did not publish results (which turned out to be correct) about what is now known as the Lamb shift. *Wik
2008 Derek Thomas "Tom" Whiteside FBA (23 July 1932 – 22 April 2008) was a British historian of mathematics. He was the foremost authority on the work of Isaac Newton and editor of The Mathematical Papers of Isaac Newton. From 1987 to his retirement in 1999, he was the Professor of History of Mathematics and Exact Sciences at Cambridge University. *Wik
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
1 comment:
Just read about a connection between Compton, the speed bump physicist, and Oppenheimer, the birthday boy today. According to Car and Driver, Compton hired Oppenheimer to run Manhattan Project.
Post a Comment