The mathematician may be compared to a designer of garments, who is utterly oblivious of the creatures whom his garments may fit. To be sure, his art originated in the necessity for clothing such creatures, but this was long ago; to this day a shape will occasionally appear which will fit into the garment as if the garment had been made for it. Then there is no end of surprise and delight.
~David van Dantzig
This is the 203rd day of the year; 203 is the 6th Bell number, i.e. it is the number of partitions of a set of size 6.
203^2 + 203^3 + 1 is prime.
203 is the number of nondegenerate triangles that can be made from rods of lengths 1,2,3,4,...,12
203 is the number of triangles pointing in opposite direction to largest triangle in triangular matchstick arrangement of side length 13
Saw a tweet about July 22 as "Casual Pi Day" at Rimwe@RimweLLC which he told me he found at page of GeorgeTakei.
The NCTM uses "Pi Approximation Day" for it's poster
203 is a palindrome in base 3 (21112)
For More Math Facts for Every Year Date
1588 Joost Burgi sent emperor Rudolph II his direct method using only simple arithmetic to produce a complete table of sines from zero to 90 degrees. I have to admit I could not imagine this working. I was shocked. I still can't explain WHY it works, but it seems to produce ever improving approximations,
1694 Johann Bernoulli sent “L’Hospital’s rule” to L’Hospital under the terms of their agreement of 17 March 1694. *VFR The agreement between them led to the first real calculus text in 1696.
1799 On March 28, 1794, the president of the French commission that developed the metric system, Joseph Louis Lagrange, proposed using the day (French jour) as the base unit of time, with divisions déci-jour and centi-jour.
In 1795, the French National Convention passed a law introducing the metric system, putting Legendre in charge of the transition to the new system. The final system, as introduced in 1795, included units for length, area, dry volume, liquid capacity, weight or mass, and currency, but not time. Decimal time of day had been introduced in France two years earlier, but was set aside at the same time the metric system was inaugurated, and did not follow the metric pattern of a base unit and prefixed units.
On 22nd July 1799 the definitive standards of the metric system, the platinum metre and the platinum kilogramme, were ceremonially deposited in the French National Archives, and on 10th December 1799 a law was passed confirming their status as the only legal standards for measuring length and mass in France.
(The combination metric and decimal clock is at the Fitzwilliam Museum in Cambridge, U.K. The metric is on the outside scale, the duodecimal is on the small enamel dial inset above the center
1900 It seems that the first to discuss the problem of constructing magic squares with prime numbers was Henry Ernest Dudeney. It was in The Weekly Dispatch, 22nd July and 5th August 1900. Unfortunately, at that time, "1" was considered as a prime number. The magic sum 111 of his 3x3 square is the lowest possible, allowing '1'." (image below)*Multimagie.com "Henri Lebesgue (1875-1941) is said to be the last professional mathematician to call 1 prime." *Prime Curios... but then "Carl Sagan included the number 1 in an example of prime numbers in his book Cosmos."
1925 After Norbert Wiener suggested to his friend Phillip Franklin in a letter that they hang a sign outside their office at MIT reading “Wiener and Franklin. Wholesale and Retail Mathematicians and Exporters,” he wrote: “As to the state of the market: differential geometry seems rather quiet, and some of the principal operators have deserted it for other securities. Real and complex variables continue firm, without much change. Analysis situs has a bull market. Bull operators have been very active in differential equations, also. Quantum theory continues speculative, with chances of a very sharp rise, but the market contains a lot of wildcat stock. Hilbert, Brouwer, and Co. are doing well with mathematical logic.” From Science in America, ed. Nathan Reingold, p. 384.*VFR
1933 Wiley Post startled the world by completing the first solo airplane flight around the world. The 15,400 mile flight lasted seven days, 18 hours, 49 and 1/2 minutes. Two years later he was killed in an airplane crash with humorist, Will Rogers. [Scientific American, November 1933]*VFR He had made an accompanied flight around the world in 1931. Born 22 Nov 1898, Wiley Post made his first solo flight in 1926, the year he got his flying license, signed by Orville Wright, despite wearing a patch over his left eye, lost in an oilfield accident. Post invented the first pressurized suit to wear when he flew around the world. Another credit was his research into the jet streams. He died with his passenger, humorist Will Rogers, 15 Aug 1935 in a plane crash in Alaska.*TIS
In 1930, the record for flying around the world was not held by a fixed-wing aircraft, but by the Graf Zeppelin, piloted by Hugo Eckener in 1929 with a time of 21 days. On June 23, 1931, Post and the Australian navigator Harold Gatty left Roosevelt Field on Long Island, New York, in the Winnie Mae with a flight plan that would take them around the world, stopping at Harbour Grace, Flintshire, Hanover twice, Berlin, Moscow, Novosibirsk, Irkutsk, Blagoveshchensk, Khabarovsk, Nome (where his propeller had to be repaired), Fairbanks (where the propeller was replaced), Edmonton, and Cleveland before returning to Roosevelt Field. They arrived back on July 1, after traveling 15,474 miles (24,903 km) in the record time of 8 days and 15 hours and 51 minutes, in the first successful aerial circumnavigation by a single-engined monoplane. *Wik
Wiley Post with Harold Gatty in Germany, 1931
 |
| *Wikipedia |
1976 “researchers from Univ of Illinois announced they had found an unavoidable set containing 1936 reducible configurations effectively proving the four color theorem.*VFR
1978 Roger Apéry gave a talk entitled "Sur l'irrationalité de ζ(3)." to outline proofs that ζ(3) and ζ(2) were irrational. Alfred J. Van der Poorten's reprint of the talk describes the less than hopeful anticipation of the audience.,
"The board of programme changes informed us that R. Apery (Caen) would speak Thursday, 14:00 ‘Sur l’irrationalit'e de ζ(3)’. Though there had been earlier rumours of his claiming a proof, scepticism was general. The lecture tended to strengthen this view to rank disbelief. Those who listened casually, or who were afflicted with being non-Francophone, appeared to hear only a sequence of unlikely assertions"
"I heard with some incredulity that, for one, Henri Cohen (then Bordeaux, now Grenoble) believed that these claims might well be valid. Very much intrigued, I joined Hendrik Lenstra (Amsterdam) and Cohen in an evening’s discussion in which Cohen explained and demonstrated most of the details of the proof. We came away convinced that Professeur Apery had indeed found a quite miraculous and magnificent demonstration of the irrationality of ζ(3)." *, Poorten, A PROOF THAT EULER MISSED , with special thanks to Tim Pentilla who helped me establish the date of the original address.
A paper on a shorter proof by Tom Apostol is here
1983 Science reported that Gerd Faltings of Wuppertal University in Germany proved the sixty-year old Mordell conjecture: most equations of degree higher than three have only a finite number of rational solutions. In particular, this applies to Fermat’s Last Theorem. [Mathematics Magazine 57 (1984), p. 52].*VFR In number theory, the Mordell conjecture is the conjecture made by Mordell (1922) that a curve of genus greater than 1 over the field Q of rational numbers has only finitely many rational points. The conjecture was later generalized by replacing Q by a finite extension. It was proved by Gerd Faltings (1983), and is now known as Faltings' theorem.
1997 Apple Announces OS 8-Apple Computer Inc. announces a new operating system for its Macintosh computers, OS 8. An important move at a time when Apple's upper-level management and profits were experiencing significant problems, the new operating system offered new features such as easier integration of the Internet and a three-dimensional look. Immediately after the announcement, the software earned positive reviews from users, although it was not expected to end Apple's financial troubles as it faced growing competition from improvements in the Microsoft Windows operating system used on IBM-compatible PCs. *CHM
 |
| *CHM |
2009 A total solar eclipse the longest-lasting total eclipse of the 21st century – takes place. It lasted a maximum of 6 minutes and 39 seconds off the coast of Southeast Asia, causing tourist interest in eastern China, Japan, India, Nepal and Bangladesh. It will not be surpassed until 13 June 2132. *Wik
The moon passes between the sun and the earth during a total solar eclipse in the northern Indian city of Varanasi July 22, 2009.
2381 The maximum theoretical length for a British total eclipse is 5.5 minutes. The eclipse of June 16, 885 lasted for almost 5 minutes and the same will be true for the Scottish total eclipse of 22 Jul, 2381. This TSE will be the first total solar eclipse in Amsterdam since 17 June 1433. *NSEC
BIRTHS
1784 Friedrich Wilhelm Bessel born (22 July 1784 – 17 March 1846). He is noted for the special class of functions that have become an indispensable tool in applied mathematics. This, like all of his mathematical work, was motivated by his work in astronomy. *VFR In 1809, at the age of 26, Bessel was appointed director of Frederick William III of Prussia's new Königsberg Observatory and professor of astronomy, where he spent the rest of his career. His monumental task was determining the positions and proper motions for about 50,000 stars, which allowed the first accurate determination of interstellar distances. Bessel's work in determining the constants of precession, nutation and aberration won him further honors. Other than the sun, he was the first to measure the distance of a star, by parallax, of 61 Cygni (1838). In mathematical analysis, he is known for his Bessel function. *TIS |
| *Linda Hall Org |
1795 Gabriel Lam´e (22 July 1795 – 1 May 1870) born in Tours, in today's département of Indre-et-Loire.
He became well known for his general theory of curvilinear coordinates and his notation and study of classes of ellipse-like curves, now known as Lamé curves, and defined by the equation:
He is also known for his running time analysis of the Euclidean algorithm. Using Fibonacci numbers, he proved that when finding the greatest common divisor of integers a and b, the algorithm runs in no more than 5k steps, where k is the number of (decimal) digits of b. He also proved a special case of Fermat's last theorem. He actually thought that he found a complete proof for the theorem, but his proof was flawed. The Lamé functions are part of the theory of ellipsoidal harmonics. *Wik
Piet Hein's Super Ellipse is a Lame Curve
1822 Gregor Mendel (July 20, 1822 – January 6, 1884) (Original name (until 1843) Johann Mendel). Austrian pioneer in the study of heredity. He spent his adult life with the Augustinian monastery in Brunn, where as a geneticist, botanist and plant experimenter, he was the first to lay the mathematical foundation of the science of genetics, in what came to be called Mendelism. Over the period 1856-63, Mendel grew and analyzed over 28,000 pea plants. He carefully studied for each their plant height, pod shape, pod color, flower position, seed color, seed shape and flower color. He made two very important generalizations from his pea experiments, known today as the Laws of Heredity. Mendel coined the present day terms in genetics: recessiveness and dominance.
1882 Konrad Knopp (22 July 1882 – 20 April 1957) born. He is best known for comprehensive book on infinite series.*VFR
1887 - Gustav Hertz born (22 July 1887 – 30 October 1975) .Hertz was a German physicist who shares the 1925 Nobel Prize in Physics with James Franck for their Frank-Hertz experiment. The Frank-Hertz experiment shows that an atom absorbs energy in discrete amounts, confirming the quantum theory of atoms. This experiment was an important step confirming the Bohr model of the atom. *TIS
1902 Reinhold Baer (July 22, 1902 – October 22, 1979) Baer's mathematical work was wide ranging; topology, abelian groups and geometry. His most important work, however, was in group theory, on the extension problem for groups, finiteness conditions, soluble and nilpotent groups.*SAU
1914 Edward (Rolke) Farber was an American who invented a portable, battery-operated stroboscopic flash unit for still cameras (1937) that effectively "stopped action." He began his career as a photojournalist on the staff of the Milwaukee Journal. After studying electrical engineering at Northwestern University, Farber went on to design flash equipment for the U.S. Army during World War II, and then established his own electronic-flash manufacturing firm. He was a good friend and collaborator of Harold Edgerton and developed the first practical portable strobe flash for news photographers. In 1942, the Milwaukee Journal became the first newspaper to furnish all of its photographers with the portable flash. Weighing only 13.5 pounds, it was a considerable improvement over the 90-pound units photographers used prior to Farber's invention. He sold his Strobe Research firm in 1954. He was a photographic adviser to the U.S. Government during its intercontinental ballistic missile testing program in the late 1950's.*TIS
1935 John Robert Stallings (July 22, 1935 – November 24, 2008) In 1968 Stallings published his most famous paper On torsion-free groups with infinitely many ends in the Annals of Mathematics. L Neuwirth explains what is contained in the paper:-
In this remarkable paper, the author, using very little besides his bare hands, proves the following theorem:
Theorem 1. If G is a torsion-free, finitely presented group, with infinitely many ends, then G is a non-trivial free product.
This simple sounding theorem proves to be very powerful, implying (with a little work) the following two theorems:
Theorem 2. A torsion-free, finitely generated group, containing a free subgroup of finite index, is itself free.
Theorem 3. A finitely generated group of cohomological dimension 1 is free.
This last theorem answers a question which had been unanswered for over ten years and which had received considerable attention over that period of time. Theorem 2 answers a question of J-P Serre, who proved an analogue of Theorem 2 for pro-p groups. The proof of Theorem 1 is both combinatorial and geometric in nature and, as suggested, is self-contained.
For this truly outstanding paper the American Mathematical Society awarded Stallings their Frank Nelson Cole Prize in Algebra in 1970. Also in 1970 he was invited to address the International Congress of Mathematicians in Nice, France. He gave a talk on Group theory and 3-manifolds. He had been honoured in the previous year when invited to give the James K Whittemore Lecture in Mathematics at Yale University in 1969. His topic was Group theory and three-dimensional manifolds. This lecture and his Nice address were both published in 1971.
Among the 50 or so papers Stalling published, we should highlight another two which have proved particularly important: Topology on finite graphs (1983) and Non-positively curved triangles of groups (1991). The first of these introduced the 'Stallings subgroup graph' as a method to describe subgroups of free groups. It also introduced a foldings technique now known as 'Stallings' foldings method' which has been the basis for much later work. The second of these two papers introduced the notion of a triangle of groups which became the basis for later work on the theory of complexes of groups.*SAU
1575 Francisco Maurolico (Messina, Sicily, 16 Sept 1494 - near Messina, Sicily, 21/22 July 1575) was an Italian Benedictine who wrote important books on Greek mathematics. He also worked on geometry, the theory of numbers, optics, conics and mechanics.*SAU
1826 Giuseppe Piazzi (July 16, 1746 – July 22, 1826) Italian astronomer and author, born in Valtellina, discovered the first asteroid - Ceres. He established an observatory at Palermo and mapped the positions of 7,646 stars. He also discovered that the star 61 Cygni had a large Proper Motion , which led Bessel to chose it as the object of his parallax studies. He discovered Ceres in 1801, but was able to make only three observations. Fortuitously, Gauss had recently developed mathematical techniques that allowed the orbit to be calculated. This was the first asteroid discovered. The thousandth Asteroid discovered was named Piazzia in his honor.*TIS (His dates of birth and death are six days apart)
1869 John A. Roebling (June 12, 1806 – July 22, 1869) German-American engineer who pioneered the design and construction of suspension bridges. In 1831 he immigrated to Saxonburg, near Pittsburgh, Pa., and shortly thereafter was employed by the Pennsylvania Railroad Corp. to survey its route across the Allegheny Mountains. He then demonstrated the practicability of steel cables in bridge construction and in 1841 established at Saxonburg the first U.S. factory to manufacture steel-wire rope. Roebling utilized steel cables in the construction of numerous suspension bridges including a railroad suspension bridge over the Niagara River at Niagara Falls (1851-55). He designed the Brooklyn Bridge. He died from injuries while supervising preliminary construction operations.*TIS
“Suspension Bridge Grand March,” sheet music cover, commemorating the opening of the Ohio River suspension bridge, designed and built by John A. Roebling, Cincinnati, 1867, Library of Congress (loc.gov)
 |
| *Linda Hall Org |
1915 Sir Sandford Fleming (January 7, 1827 – July 22, 1915) Scottish surveyor and leading railway engineer who divided world into time zones. He emigrated at age 17 years to Quebec, Canada, on April 24, 1845, as a surveyor. Later became one of the foremost railway engineers of his time. While in charge of the initial survey for the Canadian Pacific Railway, the first Canadian railway to span the continent, he realized the problems of coordinating such a long railway. This lead him to the idea of time zones, which contribution to the adoption of the present system of time zones earned him the title of "Father of Standard Time." Fleming also designed the first Canadian postage stamp. Issued in 1851, it cost three pennies and depicted the beaver, now the national animal of Canada.*TIS
1932 Reginald Aubrey Fessenden (October 6, 1866 – July 22, 1932), was a Canadian inventor and engineer with 300 patents. He broadcast the first program of voice and music. In 1893, Fessenden moved to Pittsburgh as the head of electrical engineering at the university, Fessenden read of Marconi's work and began experimenting himself. Marconi could only transmit Morse code. But Fessenden's goal was to transmit the human voice and music. He invented the "continuous wave": sound superimposed onto a radio wave for transmission. A radio receiver extracts the signal so the listener with the original sound. Fessenden made the first long-range transmissions of voice on Christmas Eve 1906 from a station at Brant Rock, Massachusetts, heard hundreds of miles out in the Atlantic.*TIS
1938 Ernest (William) Brown (29 November 1866 – 22 July 1938) was a British astronomer who devoted his career to the theory of the Moon's motion and constructing accurate lunar tables. His theory took account of "the gravitational action of every particle of matter which can have a sensible effect on the Moon's motion," some 1500 terms. He then determined the numerical values of the constants by analyzing 150 years of Greenwich observations, and computed tables accurate to 0.01 arcsec. After 30 years of work, Brown published his lunar tables Tables of the Motion of the Moon in 1919. In 1926 Brown published a paper in which he ascribed fluctuations in the Moon's motion to irregular changes in the Earth's period of rotation, which has subsequently proved correct. *TIS
1943 William Fogg Osgood died (March 10, 1864, Boston - July 22, 1943, Belmont, Massachusetts). Although his nickname was “Foggy,” this was not an apt description of him as a teacher. He instilled the habit of careful thought in Harvard students for 43 years. His A First Course in Differential and Integral Calculus (1907) was revised once and reprinted 17 times.*VFR From 1899 to 1902, he served as editor of the Annals of Mathematics and in 1904–1905 was president of the American Mathematical Society, whose Transactions he edited in 1909–1910. In 1904, he was elected to the National Academy of Sciences.
The works of Osgood dealt with complex analysis, in particular conformal mapping and uniformization of analytic functions, and calculus of variations. He was invited by Felix Klein to write an article on complex analysis in the Enzyklopädie der mathematischen Wissenschaften which was later expanded in the book Lehrbuch der Funktionentheorie. Besides his research on analysis, Osgood was also interested in mathematical physics and wrote on the theory of the gyroscope. *Wik
1959 David van Dantzig (September 23, 1900, Amsterdam – July 22, 1959) was at secondary school when he wrote his first mathematics paper. He was only thirteen years old at the time. However, his main interest in secondary school was not mathematics, rather it was chemistry. After leaving school he continued with his studies of chemistry, but this he did not enjoy and when he was forced to give up his academic studies to help support his family van Dantzig took on a number of jobs purely to make money.
By now van Dantzig knew that mathematics was the subject which he really wanted to study but he was not in a position to do so, both because he had to earn money and also because he did not have the necessary school qualifications. He put in hours of work on mathematics in the evenings after finishing his money earning tasks for the day. He took the state mathematics examinations in 1921, at a higher level the following year and again in 1923 he passed at a higher level still. Entering the University of Amsterdam to study mathematics he soon passed examinations which took him essentially to Master's Degree level.
Van Dantzig became an assistant to Schouten in 1927 at Delft Technical University. Then, for a short time, he taught at a teacher training institution, but he returned to Delft as a lecturer in 1932. This was the year in which he received his doctorate from Gröningen for a thesis which he submitted in 1931 Studiën over topologische Algebra. In this work he coined the now familiar term topological algebra but the thesis is memorable in other ways too. It -
Van Dantzig became an assistant to Schouten in 1927 at Delft Technical University. Then, for a short time, he taught at a teacher training institution, but he returned to Delft as a lecturer in 1932. This was the year in which he received his doctorate from Gröningen for a thesis which he submitted in 1931 Studiën over topologische Algebra. In this work he coined the now familiar term topological algebra but the thesis is memorable in other ways too. It -
... is a fine example of mathematical style: it consists of a concise string of definitions and theorems organised in such a way that in this context each theorem is obvious and none needs a proof.
He was promoted to extraordinary professor at Delft in 1938 and then an ordinary professor in 1940. The Dutch had tried to remain neutral when World War II broke out in 1939 but in the spring of 1940 German troops, in a strategic move on their way to attack France, entered Holland and the Dutch were defeated in a week. Van Dantzig was dismissed from his chair when the Germans occupied Holland and he was forced to move with his family from the Hague to Amsterdam.
After the war ended, he was appointed professor at the University of Amsterdam in 1946. In Amsterdam he was the cofounder of the research and service institution, the Mathematisch Centrum. He played a major role in both this Centre and in the University of Amsterdam where he continued to hold his chair until his death.
Van Dantzig studied differential geometry, electromagnetism and thermodynamics. His most important work was in topological algebra and in addition to his doctoral thesis which we mentioned above, he wrote a whole series of papers on topological algebra. He studied metrisation of groups rings and fields. One paper classified fields with a locally compact topology.*SAU
1966 Philipp Frank (20 Mar 1884; 22 Jul 1966 at age 82) Austrian-American physicist and mathematician whose theoretical work covered a broad range of mathematics, including variational calculus, Hamiltonian geometrical optics, Schrödinger wave mechanics, and relativity. Frank had a deep and lasting interest in the philosophy of science. In a number of writings, he strove to reconcile science and philosophy and “bring about the closest rapprochement between” them. The 1907 paper he wrote analyzing the law of causality caught Einstein's attention, who in 1912 recommended Frank as his successor as professor of theoretical physics at the German University of Prague. He held that position until 1938, when he moved to Harvard University in the U.S., first as visiting lecturer, but remaining there until retirement in 1954. He wrote on misinterpretations of the Theory of Relativity.*TIS
1995 Otakar Boruvka (10 May 1899 in Uherský Ostroh – 22 July 1995 in Brno) To many people Boruvka is best known for his solution of the Minimal Spanning Tree problem which he published in 1926 in two papers On a certain minimal problem (Czech) and Contribution to the solution of a problem of economical construction of electrical networks (Czech). Let us quote the problem as it appears in the second of these 1926 papers:-
There are n points in the plane whose mutual distances are different. The problem is to join them with a net in such a way that:
1. any two points are joined to each other either directly or by means of some other points;
2. the total length of the net will be minimal.
In modern graph theoretical terms this can be stated as: Given an undirected graph with weights assigned to its edges, find a spanning tree of minimal weight.
In fact the problem had been suggested to Boruvka before he became a university student. He had a friend, Jindrich Saxel, who worked for the firm West-Moravian Powerplants and he suggested the problem which he stated in terms of cities and the distances between them. At the time that Saxel suggested the problem to Boruvka, World War I was still happening and Czech universities were closed. Boruvka was offered a job with West-Moravian Powerplants at this time but declined. The authors write:-
The Minimal Spanning Tree problem is a cornerstone of Combinatorial Optimisation and in a sense its cradle. The problem is important both in its practical and theoretical applications. Moreover, recent development places Boruvka's pioneering work in a new and very contemporary context. One can even say that out of many available Minimal Spanning Tree algorithms, Boruvka's algorithm is presently the basis of the fastest known algorithms. *SAU
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
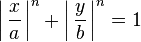
No comments:
Post a Comment