"Yet I exist in the hope that these memoirs ...
may find their way to the minds of humanity in Some Dimensions,
and may stir up a race of rebels who shall refuse to be confined to limited Dimensionality."
~ Edwin Abbott Abbott, FlatlandThe 285th day of the year, 285 is a square pyramidal number (like a stack of cannonballs, or oranges with the base in a square)... Or.. the sum of the first nine squares.
285 is 555 in base 7.
Not sure how rare this is, but just saw it on MAA's Number a Day and was intrigued, 285^2 = 81225 uses the same digits as 135^2 (18225) and 159^2 (25281).
A number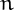 
is said to be anti-perfect if it is equal to the sum of the reverses of its proper divisors.
EVENTS
1793 At the University of North Carolina, the cornerstone was laid for “Old East,” the oldest state university building in the U.S.*VFR
1810 the German festival Oktoberfest was first held in Munich. Reaallly good ideas WILL spread.
1850, classes began at the Women's Medical College of Pennsylvania, the first medical school entirely for women.*TIS
1884 George Bruce Halsted presented his inaugural address before the Texas Academy of Science. He spoke of his teacher at Johns Hopkins, J. J. Sylvester, and related how the rumor started that Sylvester killed a student when he was at the university of Virginia. [Science, 22 February 1885; vol. 1, no. 8, p. 265] *VFR
1988 Steve Jobs unveiled the NeXT, the computer he designed after moving on from Apple Computer Inc., which he had founded with Steve Wozniak. Although the NeXT ultimately failed, it introduced several features new to personal computers, including an optical storage disk, a built-in digital signal processor that allowed voice recognition, and object-oriented languages that simplified programming. On a microprocessor with 8 megabytes of RAM, however, the NeXT ran too slowly to be popular. NeXT Computer Inc. eventually became NeXT Software Inc. and then was bought by Apple in 1997.
1996: A solar eclipse was broadcast live on the internet for the first time. * BBC Archive @BBCArchive
BIRTHS
1860 Elmer Sperry (12 Oct 1860; 16 Jun 1930) American electrical engineer and inventor of the gyrocompass. In the 1890's he made useful inventions in electric mining machinery, and patent electric brake and control system for street- or tramcars. In 1908, he patented the active gyrostabilizer which acted to stop a ship's roll as soon as it started. He patented the first gyrocompass designed expressly for the marine environment in 1910. This "spinning wheel" gyro was a significant improvement over the traditional magnetic compass of the day and changed the course of naval history. The first Sperry gyrocompass was tested at-sea aboard the USS Delaware in 1911 and established Sperry as a world leader in the manufacture of military gyrocompasses for the next 80 years. *TIS
DEATHS
1492 Piero della Francesca (June 1420, 12 Oct 1492) was an Italian artist who pioneered the use of perspective in Renaissance art and went on to write several mathematical treatises. In his own time he was also known as a highly competent mathematician. In his Lives of the most famous painters ... [13], Giorgio Vasari (1511-1572) says that Piero showed mathematical ability in his earliest youth and went on to write 'many' mathematical treatises. Of these, three are now known to survive. The titles by which they are known are: Abacus treatise (Trattato d'abaco), Short book on the five regular solids (Libellus de quinque corporibus regularibus) and On perspective for painting (De prospectiva pingendi). Piero almost certainly wrote all three works in the vernacular (his native dialect was Tuscan), and all three are in the style associated with the tradition of 'practical mathematics', that is, they consist largely of series of worked examples, with rather little discursive text.
The Abacus treatise is similar to works used for instructional purposes in 'Abacus schools'. It deals with arithmetic, starting with the use of fractions, and works through series of standard problems, then it turns to algebra, and works through similarly standard problems, then it turns to geometry and works through rather more problems than is standard before (without warning) coming up with some entirely original three-dimensional problems involving two of the 'Archimedean polyhedra' (those now known as the truncated tetrahedron and the cuboctahedron).
Four more Archimedeans appear in the Short book on the five regular solids: the truncated cube, the truncated octahedron, the truncated icosahedron and the truncated dodecahedron. (All these modern names are due to Johannes Kepler (1619).) Piero appears to have been the independent re-discoverer of these six solids. Moreover, the way he describes their properties makes it clear that he has in fact invented the notion of truncation in its modern mathematical sense.
On perspective for painting is the first treatise to deal with the mathematics of perspective, a technique for giving an appearance of the third dimension in two-dimensional works such as paintings or sculptured reliefs. Piero is determined to show that this technique is firmly based on the science of vision (as it was understood in his time). He accordingly starts with a series of mathematical theorems, some taken from the optical work of Euclid (possibly through medieval sources) but some original to Piero himself. Some of these theorems are of independent mathematical interest, but on the whole the work is conceived as a manual for teaching painters to draw in perspective, and the detailed drawing instructions are mind-numbing in their repetitiousness. There are many diagrams and illustrations, but unfortunately none of the known manuscripts has illustrations actually drawn by Piero himself.
None of Piero's mathematical work was published under his own name in the Renaissance, but it seems to have circulated quite widely in manuscript and became influential through its incorporation into the works of others. Much of Piero's algebra appears in Pacioli's Summa (1494), much of his work on the Archimedeans appears in Pacioli's De divina proportione (1509), and the simpler parts of Piero's perspective treatise were incorporated into almost all subsequent treatises on perspective addressed to painters. *SAU
1682 Jean-Felix Picard (July 21, 1620 – July 12, 1682) was a French astronomer and priest born in La Flèche, where he studied at the Jesuit Collège Royal Henry-Le-Grand. He was the first person to measure the size of the Earth to a reasonable degree of accuracy in a survey conducted in 1669–70, for which he is honored with a pyramid at Juvisy-sur-Orge. Guided by Maurolycus's methodology and Snellius's mathematics for doing so, Picard achieved this by measuring one degree of latitude along the Paris Meridian using triangulation along thirteen triangles stretching from Paris to the clocktower of Sourdon, near Amiens. His measurements produced a result of 110.46 km for one degree of latitude, which gives a corresponding terrestrial radius of 6328.9 km. The polar radius has now been measured at just over 6357 km. This was an error only 0.44% less than the modern value. This was another example of advances in astronomy and its tools making possible advances in cartography. Picard was the first to attach a telescope with crosswires (developed by William Gascoigne) to a quadrant, and one of the first to use a micrometer screw on his instruments. The quadrant he used to determine the size of the Earth had a radius of 38 inches and was graduated to quarter-minutes. The sextant he used to find the meridian had a radius of six feet, and was equipped with a micrometer to enable minute adjustments. These equipment improvements made the margin of error only ten seconds, as opposed to Tycho Brahe's four minutes of error. This made his measurements 24 times more accurate. Isaac Newton was to use this value in his theory of universal gravitation.
Picard also travelled to Tycho Brahe's Danish observatory, Uraniborg, in order to assess its position accurately so that Tycho's readings could be compared to others'. Picard collaborated and corresponded with many scientists, including Isaac Newton, Christiaan Huygens, Ole Rømer, Rasmus Bartholin, Johann Hudde, and even his main competitor, Giovanni Cassini, although Cassini was often less than willing to return the gesture. These correspondences led to Picard's contributions to areas of science outside the field of geodesy, such as the aberration of light he observed while in Uraniborg, or his discovery of mercurial phosphorescence upon his observance of the faint glowing of a barometer. This discovery led to Newton's studies of spectrometry.
Picard also developed what became the standard method for measuring the right ascension of a celestial object. In this method, the observer records the time at which the object crosses the observer's meridian. Picard made his observations using the precision pendulum clock that Dutch physicist Christiaan Huygens had recently developed. His book "Mesure de la Terre" was published in 1671.*Wik
1912 Lewis Boss (26 Oct 1846, 12 Oct 1912) American astronomer best known for his compilation of two catalogues of stars (1910, 1937). In 1882 he led an expedition to Chile to observe a transit of Venus. About 1895 Boss began to plan a general catalog of stars, giving their positions and motions. After 1906, the project had support from the Carnegie Institution, Washington, D.C. With an enlarged staff he observed the northern stars from Albany and the southern stars from Argentina. With the new data, he corrected catalogs that had been compiled in the past, and in 1910 he published the Preliminary General Catalogue of 6,188 Stars for the Epoch 1900. The work unfinished upon his death was completed by his son Benjamin in 1937*TIS
1926 Edwin Abbott Abbott (20 Dec 1838, 12 Oct 1926) His most famous work was Flatland: a romance of many dimensions (1884) which Abbott wrote under the pseudonym of A Square. The book has seen many editions, the sixth edition of 1953 being reprinted by Princeton University Press in 1991 with an introduction by Thomas Banchoff. Flatland is an account of the adventures of A Square in Lineland and Spaceland. In it Abbott tries to popularise the notion of multidimensional geometry but the book is also a clever satire on the social, moral, and religious values of the period.
More recently, in 2002, an annotated version of Flatland has been produced with an introduction and notes by Ian Stewart who gives extensive discussion of mathematical topics related to passages in Abbott's text. *SAU The Kindle edition of Flatland is available for less than $2.00 Flatland: A Romance of Many Dimensions [Illustrated]
and the Stewart version is only a little more:
In a bold statement of personal opinion I add: This book should be read by every teacher and every student of mathematics.
1936 William Sheppard read Mathematics at Cambridge and then went on to study Law. He was appointed to the Department of Education. His mathematical interests were mainly in Statistics. *SAU
1984 Georgii Dmitrievic Suvorov (19 May 1919, 12 Oct 1984) made major contributions to the theory of functions. He worked, in particular, on the theory of topological and metric mappings on 2-dimensional space. Another area on which Suvorov worked was the theory of conformal mappings and quasi-formal mappings. His results in this area, mostly from the late 1960s when he was at Donetsk, are of particular significance. He extended Lavrentev's results in this area, in particular Lavrentev's stability and differentiability theorems, to more general classes of transformations. One of the many innovations in Suvorov's work was new methods which he introduced to help in the understanding of metric properties of mappings with bounded Dirichlet integral. *SAU
2011 Dennis MacAlistair Ritchie (September 9, 1941; found dead October 12, 2011), was an American computer scientist who "helped shape the digital era." He created the C programming language and, with long-time colleague Ken Thompson, the UNIX operating system. Ritchie and Thompson received the Turing Award from the ACM in 1983, the Hamming Medal from the IEEE in 1990 and the National Medal of Technology from President Clinton in 1999. Ritchie was the head of Lucent Technologies System Software Research Department when he retired in 2007. He was the 'R' in K&R C and commonly known by his username dmr. *Wik
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
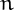is said to be anti-perfect if it is equal to the sum of the reverses of its proper divisors.For example, 244 is anti-perfect since its proper divisors are 1, 2, 4, 61, 122 and the sum of their reversal is 1 + 2 + 4 + 16 + 221 = 244.
The known anti-perfect numbers are 6, 244, 285, 133857, 141635817 *Numbers aplenty
1793 At the University of North Carolina, the cornerstone was laid for “Old East,” the oldest state university building in the U.S.*VFR
1810 the German festival Oktoberfest was first held in Munich. Reaallly good ideas WILL spread.
1850, classes began at the Women's Medical College of Pennsylvania, the first medical school entirely for women.*TIS
1884 George Bruce Halsted presented his inaugural address before the Texas Academy of Science. He spoke of his teacher at Johns Hopkins, J. J. Sylvester, and related how the rumor started that Sylvester killed a student when he was at the university of Virginia. [Science, 22 February 1885; vol. 1, no. 8, p. 265] *VFR
1988 Steve Jobs unveiled the NeXT, the computer he designed after moving on from Apple Computer Inc., which he had founded with Steve Wozniak. Although the NeXT ultimately failed, it introduced several features new to personal computers, including an optical storage disk, a built-in digital signal processor that allowed voice recognition, and object-oriented languages that simplified programming. On a microprocessor with 8 megabytes of RAM, however, the NeXT ran too slowly to be popular. NeXT Computer Inc. eventually became NeXT Software Inc. and then was bought by Apple in 1997.
1996: A solar eclipse was broadcast live on the internet for the first time. * BBC Archive @BBCArchive
1860 Elmer Sperry (12 Oct 1860; 16 Jun 1930) American electrical engineer and inventor of the gyrocompass. In the 1890's he made useful inventions in electric mining machinery, and patent electric brake and control system for street- or tramcars. In 1908, he patented the active gyrostabilizer which acted to stop a ship's roll as soon as it started. He patented the first gyrocompass designed expressly for the marine environment in 1910. This "spinning wheel" gyro was a significant improvement over the traditional magnetic compass of the day and changed the course of naval history. The first Sperry gyrocompass was tested at-sea aboard the USS Delaware in 1911 and established Sperry as a world leader in the manufacture of military gyrocompasses for the next 80 years. *TIS
1492 Piero della Francesca (June 1420, 12 Oct 1492) was an Italian artist who pioneered the use of perspective in Renaissance art and went on to write several mathematical treatises. In his own time he was also known as a highly competent mathematician. In his Lives of the most famous painters ... [13], Giorgio Vasari (1511-1572) says that Piero showed mathematical ability in his earliest youth and went on to write 'many' mathematical treatises. Of these, three are now known to survive. The titles by which they are known are: Abacus treatise (Trattato d'abaco), Short book on the five regular solids (Libellus de quinque corporibus regularibus) and On perspective for painting (De prospectiva pingendi). Piero almost certainly wrote all three works in the vernacular (his native dialect was Tuscan), and all three are in the style associated with the tradition of 'practical mathematics', that is, they consist largely of series of worked examples, with rather little discursive text.
The Abacus treatise is similar to works used for instructional purposes in 'Abacus schools'. It deals with arithmetic, starting with the use of fractions, and works through series of standard problems, then it turns to algebra, and works through similarly standard problems, then it turns to geometry and works through rather more problems than is standard before (without warning) coming up with some entirely original three-dimensional problems involving two of the 'Archimedean polyhedra' (those now known as the truncated tetrahedron and the cuboctahedron).
Four more Archimedeans appear in the Short book on the five regular solids: the truncated cube, the truncated octahedron, the truncated icosahedron and the truncated dodecahedron. (All these modern names are due to Johannes Kepler (1619).) Piero appears to have been the independent re-discoverer of these six solids. Moreover, the way he describes their properties makes it clear that he has in fact invented the notion of truncation in its modern mathematical sense.
On perspective for painting is the first treatise to deal with the mathematics of perspective, a technique for giving an appearance of the third dimension in two-dimensional works such as paintings or sculptured reliefs. Piero is determined to show that this technique is firmly based on the science of vision (as it was understood in his time). He accordingly starts with a series of mathematical theorems, some taken from the optical work of Euclid (possibly through medieval sources) but some original to Piero himself. Some of these theorems are of independent mathematical interest, but on the whole the work is conceived as a manual for teaching painters to draw in perspective, and the detailed drawing instructions are mind-numbing in their repetitiousness. There are many diagrams and illustrations, but unfortunately none of the known manuscripts has illustrations actually drawn by Piero himself.
None of Piero's mathematical work was published under his own name in the Renaissance, but it seems to have circulated quite widely in manuscript and became influential through its incorporation into the works of others. Much of Piero's algebra appears in Pacioli's Summa (1494), much of his work on the Archimedeans appears in Pacioli's De divina proportione (1509), and the simpler parts of Piero's perspective treatise were incorporated into almost all subsequent treatises on perspective addressed to painters. *SAU
1682 Jean-Felix Picard (July 21, 1620 – July 12, 1682) was a French astronomer and priest born in La Flèche, where he studied at the Jesuit Collège Royal Henry-Le-Grand. He was the first person to measure the size of the Earth to a reasonable degree of accuracy in a survey conducted in 1669–70, for which he is honored with a pyramid at Juvisy-sur-Orge. Guided by Maurolycus's methodology and Snellius's mathematics for doing so, Picard achieved this by measuring one degree of latitude along the Paris Meridian using triangulation along thirteen triangles stretching from Paris to the clocktower of Sourdon, near Amiens. His measurements produced a result of 110.46 km for one degree of latitude, which gives a corresponding terrestrial radius of 6328.9 km. The polar radius has now been measured at just over 6357 km. This was an error only 0.44% less than the modern value. This was another example of advances in astronomy and its tools making possible advances in cartography. Picard was the first to attach a telescope with crosswires (developed by William Gascoigne) to a quadrant, and one of the first to use a micrometer screw on his instruments. The quadrant he used to determine the size of the Earth had a radius of 38 inches and was graduated to quarter-minutes. The sextant he used to find the meridian had a radius of six feet, and was equipped with a micrometer to enable minute adjustments. These equipment improvements made the margin of error only ten seconds, as opposed to Tycho Brahe's four minutes of error. This made his measurements 24 times more accurate. Isaac Newton was to use this value in his theory of universal gravitation.
Picard also travelled to Tycho Brahe's Danish observatory, Uraniborg, in order to assess its position accurately so that Tycho's readings could be compared to others'. Picard collaborated and corresponded with many scientists, including Isaac Newton, Christiaan Huygens, Ole Rømer, Rasmus Bartholin, Johann Hudde, and even his main competitor, Giovanni Cassini, although Cassini was often less than willing to return the gesture. These correspondences led to Picard's contributions to areas of science outside the field of geodesy, such as the aberration of light he observed while in Uraniborg, or his discovery of mercurial phosphorescence upon his observance of the faint glowing of a barometer. This discovery led to Newton's studies of spectrometry.
Picard also developed what became the standard method for measuring the right ascension of a celestial object. In this method, the observer records the time at which the object crosses the observer's meridian. Picard made his observations using the precision pendulum clock that Dutch physicist Christiaan Huygens had recently developed. His book "Mesure de la Terre" was published in 1671.*Wik
1912 Lewis Boss (26 Oct 1846, 12 Oct 1912) American astronomer best known for his compilation of two catalogues of stars (1910, 1937). In 1882 he led an expedition to Chile to observe a transit of Venus. About 1895 Boss began to plan a general catalog of stars, giving their positions and motions. After 1906, the project had support from the Carnegie Institution, Washington, D.C. With an enlarged staff he observed the northern stars from Albany and the southern stars from Argentina. With the new data, he corrected catalogs that had been compiled in the past, and in 1910 he published the Preliminary General Catalogue of 6,188 Stars for the Epoch 1900. The work unfinished upon his death was completed by his son Benjamin in 1937*TIS
1926 Edwin Abbott Abbott (20 Dec 1838, 12 Oct 1926) His most famous work was Flatland: a romance of many dimensions (1884) which Abbott wrote under the pseudonym of A Square. The book has seen many editions, the sixth edition of 1953 being reprinted by Princeton University Press in 1991 with an introduction by Thomas Banchoff. Flatland is an account of the adventures of A Square in Lineland and Spaceland. In it Abbott tries to popularise the notion of multidimensional geometry but the book is also a clever satire on the social, moral, and religious values of the period.
More recently, in 2002, an annotated version of Flatland has been produced with an introduction and notes by Ian Stewart who gives extensive discussion of mathematical topics related to passages in Abbott's text. *SAU The Kindle edition of Flatland is available for less than $2.00 Flatland: A Romance of Many Dimensions [Illustrated]
and the Stewart version is only a little more:In a bold statement of personal opinion I add: This book should be read by every teacher and every student of mathematics.
1936 William Sheppard read Mathematics at Cambridge and then went on to study Law. He was appointed to the Department of Education. His mathematical interests were mainly in Statistics. *SAU
1984 Georgii Dmitrievic Suvorov (19 May 1919, 12 Oct 1984) made major contributions to the theory of functions. He worked, in particular, on the theory of topological and metric mappings on 2-dimensional space. Another area on which Suvorov worked was the theory of conformal mappings and quasi-formal mappings. His results in this area, mostly from the late 1960s when he was at Donetsk, are of particular significance. He extended Lavrentev's results in this area, in particular Lavrentev's stability and differentiability theorems, to more general classes of transformations. One of the many innovations in Suvorov's work was new methods which he introduced to help in the understanding of metric properties of mappings with bounded Dirichlet integral. *SAU
2011 Dennis MacAlistair Ritchie (September 9, 1941; found dead October 12, 2011), was an American computer scientist who "helped shape the digital era." He created the C programming language and, with long-time colleague Ken Thompson, the UNIX operating system. Ritchie and Thompson received the Turing Award from the ACM in 1983, the Hamming Medal from the IEEE in 1990 and the National Medal of Technology from President Clinton in 1999. Ritchie was the head of Lucent Technologies System Software Research Department when he retired in 2007. He was the 'R' in K&R C and commonly known by his username dmr. *Wik
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell
No comments:
Post a Comment